Niektóre normy – jak np. EN 1288 – przedstawiają wymagania dotyczące badań wytrzymałościowych szkła.
Wymagania te przy tym odnoszą się z jednej strony do tzw. dwupierścieniowych prób wytrzymałości 1) formatek szkła, bez uwzględnienia wpływu obróbki ich krawędzi, z drugiej zaś – obejmują one badania wytrzymałościowe formatek szkła poddanych zginaniu czteropunktowemu z uwzględnieniem rodzaju obróbki ich krawędzi.
Obydwa te rodzaje badań opisano przy założeniu, że przebiegają one w warunkach doskonałych, tzn. np. przy założeniu jednorodności szkła oraz pominięciu wpływu czynników występujących w warunkach rzeczywistych.
Wprowadzenie
Punktem zainteresowania jest rozkład naprężeń szczątkowych zarówno wewnątrz szkła (na grubości formatki), jak i na jego powierzchni. Naprężenia wewnętrzne zawierają naprężenia wstępne wywołane w szkle w wyniku poddania go procesom termicznym lub chemicznym. Elastooptyczne badania rozkładu naprężeń w szkle półhartowanym (wzmacnianym termicznie) lub też w pełni hartowanym szkle bezpiecznym wskazują na fakt, że na powierzchni szkła rozkład ten nie jest jednorodny.
Ów zmienny rozkład obrazują szare pasy widoczne w świetle spolaryzowanym. Niniejsze opracowanie poświęcone jest dyskusji na temat wspomnianego obrazu szarych pasów, czynników rzeczywistych oraz naprężeń, zmierzonych przy użyciu służącego do ich pomiaru urządzenia SCALP 2). Omówione tu badanie pomaga nam znacznie lepiej zrozumieć przyczyny wpływające na lokalizację punktów, w których dochodzi do pękania szkła.
Obróbka cieplna
Prowadzona zgodnie z normą EN 12150 [1] lub EN 1263 [2] obróbka cieplna stanowi typowy proces wytwarzania w szkle naprężeń wstępnych. W trakcie tego procesu ułożone na rolkach formatki szkła są wprowadzane do strefy nagrzewania pieca i ogrzewane do temperatury przekraczającej temperaturę punktu przemianym(ok. 650oC).
Po nagrzaniu szkła do wymaganej temperatury jest ono oziębiane wytwarzanym przez wentylatory strumieniem powietrza. Podczas fazy schładzania formatek szkła do temperatury otoczenia spoczywające na rolkach szkło porusza się stale ruchem wahadłowym, aż do chwili osiągnięcia wylotu z pieca. Im cieńsze są hartowane formatki szkła tym większa może być falistość powierzchni szkła wywołana odciskami rolek.
Z tego względu przeprowadzono badania procesu hartowania szkła, w którym szkło przemieszczane jest na poduszce powietrznej. Ta technologia stwarza możliwość hartowania cieńszych formatek szkła i wywoływanie w nich naprężeń wstępnych z jednoczesnym uniknięciem wywołanej rolkami falistości powierzchni.
Obróbka chemiczna – wymiana jonowa
Inna możliwość wywoływania w szkle naprężeń wstępnych polega na wykorzystaniu obróbki chemicznej, prowadzonej zgodnie z wymogami normy EN 12337 [3]. W trakcie procesu obróbki chemicznej szkło zanurzone jest w kąpieli roztopionego azotanu potasu. W temperaturze rzędu 370-450°C zachodzi zjawisko wymiany jonowej.
Jony sodu, o niewielkim promieniu jonowym, dyfundują ze szkła do kąpieli azotanu potasu, natomiast posiadające większy promień jonowy 3) jony potasu penetrują do wnętrza formatki szkła. Z uwagi na fakt, że jonowy promień jonów potasu jest większy w przypowierzchniowej warstwie szkła, powstają naprężenia ściskające. Głębokość penetracji jonowej – tzw. głębokość warstwy zdyfundowanej – waha się w granicach 30-100 μm [4].
Oznaczanie wytrzymałości na zginanie– metody badań
Wartości wytrzymałości na zginanie szkła cienkiego o grubości formatki mniejszej niż 2 mm są nadal nieznane – choć mają one podstawowe znaczenie na etapie opracowywania projektów budowlanych. Z tego też względu kilka różnych metod badań przetestowano pod kątem ich przydatności do oznaczania granicznej wytrzymałości cienkiego szkła na zginanie.
Ze względów praktycznych konieczne jest również wprowadzenie rozróżnienia pomiędzy tymi metodami badawczymi, które uwzględniają i tymi, które pomijają wpływ rodzaju obróbki krawędzi formatki szkła (jakości krawędzi), określany też mianem „efektu brzegowego”. Poniżej omówiono kilka metod badawczych możliwych do zastosowania w praktyce.
Metoda dwupierścieniowa – EN 1288-2
W wypadku metody dwupierścieniowej konfiguracja stanowiska badawczego przedstawia się następująco: badaną formatkę szkła układa się na kołowym, stalowym pierścieniu oporowym (podporze pierścieniowej), po czym na górną powierzchnię badanej formatki nakłada się stalowy pierścień przenoszący obciążenie.
Przenoszone na formatkę obciążenie zwiększa się tak długo, aż nastąpi pęknięcie szkła. Celem tak przeprowadzonego badania jest uzyskanie równomiernego (jednolitego) pola naprężeń rozciągających wewnątrz pierścienia przenoszącego obciążenie, niezależnie od jakości obróbki krawędzi formatki. Jak wskazuje w swym opracowaniu J. Neugebauer [5], opisane w normie EN 1288 metody badawcze nie zdają egzaminu w wypadku badań cienkich formatek szkła.
Nakładka silikonowa (dociskowa)
W formie udoskonalenia stanowiska badawczego stosowanego w metodzie dwupierścieniowej przetestowano możliwość użycia silikonowej nakładki dociskowej. W tym wypadku badana formatka szkła układana jest na kołowym, stalowym pierścieniu oporowym (stanowiącym podporę), obciążenie zaś przenoszone jest na górną powierzchnię formatki nie poprzez górny pierścień, lecz przez umieszczaną w tym celu na formatce nakładkę silikonową (dociskową), przy czym w trakcie badania obciążenie jest zwiększane aż do momentu pęknięcia szkła.
Korzyścią takiej konfiguracji stanowiska badawczego jest fakt, że zastosowanie nakładki pozwala na uzyskanie równomiernego rozkładu naprężeń w centralnej części badanej formatki. [5]
1) badanie powszechnie stosowane przy określaniu wytrzymałości szkła i przeprowadzane w ten sposób, że dolna powierzchnia badanej formatki opiera się na pierścieniu, zaś na górną powierzchnię nakłada się
drugi pierścień, do którego przykłada się obciążenie i który ma mniejszy promień oraz jest usytuowany (zazwyczaj) współśrodkowo względem pierścienia dolnego.
2) jest to współpracujący z komputerem i odznaczający się zwartą budową polaryskop światła rozproszonego służący do pomiaru naprężeń wzdłuż grubości formatki szkła płaskiego. Zawiera półprzewodnikową diodę laserową, układ optyczny i kamerę.
3) w wypadku jonów utworzonych z jednego atomu jest to odległość najbardziej oddalonych elektronów od jądra tego atomu; w wypadku jonów złożonych z większej liczby atomów – od geometrycznego środka.
Badanie wytrzymałościowe metodą zginania czteropunktowego wg EN 1288-3
W wypadku czteropunktowego zginania cienkiego szkła dochodzi do znacznych ugięć oraz zmiany kierunku działania sił reakcji podpór z pionowego na skośny.
Działająca na formatkę szkła siła reakcji podpór rozkłada się jedynie wzdłuż linii styku szkło-podpory, zaś pod koniec badania może się okazać konieczne uwzględnienie sił tarcia pomiędzy szkłem a gumą (kauczukiem etylenowo-propylenowym).
Z uwagi na małą grubość cienkich formatek szkła może się bowiem zdarzyć, że pod koniec próby wytrzymałościowej nie dojdzie do pęknięcia szkła, ponieważ wskutek znacznego ugięcia formatki jej krawędzie ześlizną się z podpór (odległość między podporami jest stała, a przy znacznym ugięciu krawędzie formatki zbliżają się do siebie). Do pęknięcia szkła może również nie dojść z uwagi na własności użytej do badania maszyny wytrzymałościowej – np. jeśli tłok takiej maszyny osiągnie swój maksymalny skok zanim szkło pęknie [5].
Zginanie w warunkach działania siły osiowej
Wartość wytrzymałości na zginanie można – na przykład – określić w oparciu o próbę stateczności (stabilności). Maksymalne naprężenia powstające pod wpływem działania sił F na ramieniu e można oznaczyć bazując na teorii dużych odkształceń.
Oprócz koncepcji wywołania stanu naprężeń odpowiadającego zginaniu poprzez przyłożenie do badanej próbki obciążenia do niej prostopadłego, istnieje koncepcja alternatywna, zgodnie z którą obciążenie przykładane jest do badanej próbki w jej płaszczyźnie, natomiast naprężenia zginające są wywoływane w próbce wskutek jej wyboczenia [5].
Zginanie ze stałym promieniem
Zamiast – jak to opisano wyżej – przykładać obciążenie do badanej próbki w jej płaszczyźnie, można również zastosować obciążenie wywołane poprzez obrót leżących naprzeciw siebie krótszych boków formatki w połączeniu ze zmniejszaniem odległości pomiędzy podporami przegubowymi, jak to przedstawiono w opracowaniu J. Neugebauera [5].
Dzięki dokładnej regulacji długości „cięciwy łuku”, jaką stanowi odległość pomiędzy podporami przegubowymi wygiętej łukowato próbki szkła, oraz przyłożonego momentu obrotowego, można uzyskać stały rozkład naprężeń na prawie całej długości poddanych zginaniu krawędzi (z wykluczeniem wąskiego paska brzegowego prostoliniowych krawędzi stanowiącego strefę przyłożenia momentu obrotowego) [5].
Rozkład naprężeń na powierzchni
Anizotropia
Ogólnie rzecz biorąc, zjawisko anizotropii można zdefiniować jako charakterystyczną cechę materiału polegającą na tym, że zmienia on swoje własności (jak np. wytrzymałość na rozciąganie, przewodnictwo elektryczne lub współczynnik załamania światła) w zależności od kierunku, w jakim są one rozpatrywane.
W przypadku szkła anizotropia jest rezultatem obecności światła spolaryzowanego w naturalnym środowisku, a dwójłomność szkła – z anizotropii współczynnika załamania światła pod wpływem wywołanych w szkle naprężeń (fotoelastyczność) oraz wstępnych naprężeń mechanicznych wywołanych w szkle w procesie jego obróbki termicznej [6].
Aby lepiej zrozumieć to zachowanie szkła, poddano je badaniom, z wywołanymi w nim naprężeniami wstępnymi, opartym o wykorzystanie fizycznego zjawiska polaryzacji. W wypadku bezpiecznego szkła hartowanego pojawia się tzw. „wzór pasków zebry”, którego odwzorowanie przedstawia zamieszczony niżej rys. 1.
W objętym badaniem szkle o grubości 8 mm wstępne naprężenia wywołano w procesie hartowania przeprowadzonym w konwencjonalnym piecu hartowniczym, w którym szkło było transportowane na rolkach. W niektórych punktach naprężenia wewnętrzne zmierzono przy użyciu urządzenia pomiarowego SCALP.
Wykres zamieszczony na rys. 1 wskazuje na fakt, że zmierzone naprężenia wewnętrzne nie są jednorodne wzdłuż powierzchni badanego szkła. W tym konkretnym wypadku naprężenia ściskające zmierzone na powierzchni szkła wahały się w granicach pomiędzy σ=-102,8 oraz σ=-107,5 MPa.
W procesie oznaczania wytrzymałości szkła na zginanie oraz w dyskusji uzyskanych wyników należy koniecznie uwzględnić rozkłady owych wywołanych procesem hartowania wstępnych naprężeń wewnętrznych.
Wpływ na wytrzymałość szkła na zginanie ma jednakże nie tylko rozkład naprężeń na powierzchni badanej formatki szkła. Należy uwzględnić także rozkład naprężeń na jej grubości.
Rozkład naprężeń na grubości szkła
Rozkład naprężeń mierzony wzdłuż grubości formatki szkła charakteryzuje się obecnością naprężeń ściskających na powierzchniach szkła oraz naprężeń rozciągających wewnątrz badanej formatki (w tzw rdzeniu płyty szklanej).
Na rys. 2 przedstawiono porównanie naprężeń wstępnych obecnych w formatce szkła hartowanego termicznie oraz naprężeń wstępnych wywołanych procesem chemicznej obróbki szkła.
Ogólnie rzecz biorąc, na powierzchni szkła sodowo- wapniowego wzmacnianego chemicznie występują naprężenia ściskające σ o wartości wynoszącej około -300 MPa; jednakże strefa ściskania jest bardzo cienka, jej grubość wynosi bowiem 50 μm (0,05 mm).
W specjalnym szkle aluminiowo- krzemianowym można wywołać wstępne naprężenia ściskające sięgające wartości σ= -1000 MPa.
W porównaniu do szkła wzmacnianego chemicznie wstępne naprężenia wewnętrzne występujące w szkle hartowanym termicznie wynoszą około σ=-120 MPa. Jednakże w przypadku szkła hartowanego termicznie grubość strefy ściskania wynosi około 0,2 d (20% grubości badanej formatki szkła).
Naprężenia rozciągające występujące w części środkowej (rdzeniu) formatki szkła są znacznie mniejsze od analogicznych naprężeń występujących w bezpiecznym szkle hartowanym. Stworzenie opisanego tu modelu rozkładu naprężeń było możliwe przy użyciu oprogramowania opartego na metodzie elementów skończonych.
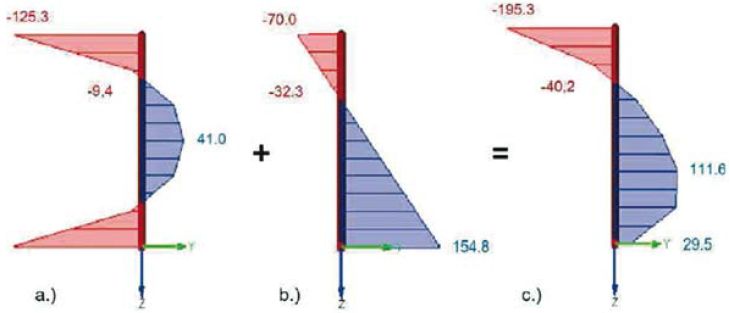
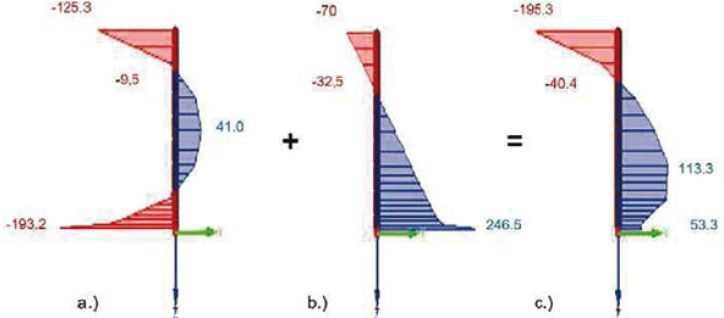
Przedstawiony na rys. 3 wykres (a) ilustruje rozkład naprężeń wstępnych występujących w szkle termicznie hartowanym. Na powierzchni szkła występują naprężenia ściskające o wartości σ=-125,3 MPa, natomiast naprężenia rozciągające występujące w części środkowej (rdzeniu) badanej formatki szkła wynoszą σ=41 MPa.
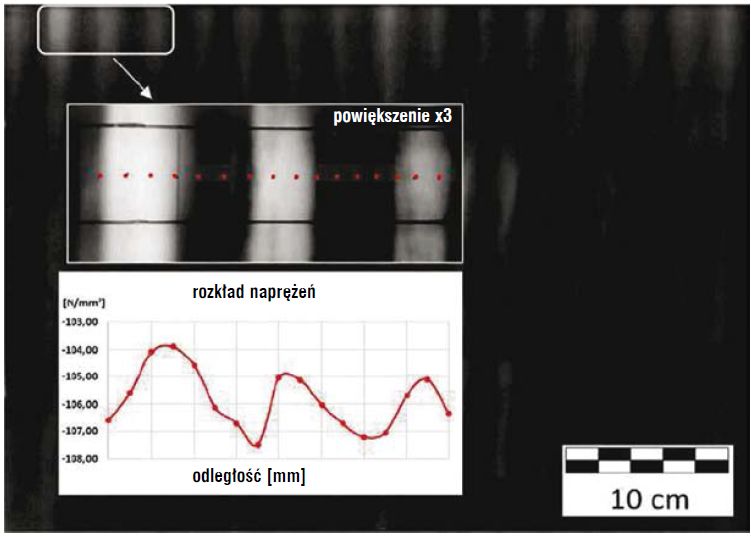
Rys. 1. Rozkład naprężeń wewnętrznych w bezpiecznym szkle hartowanym.
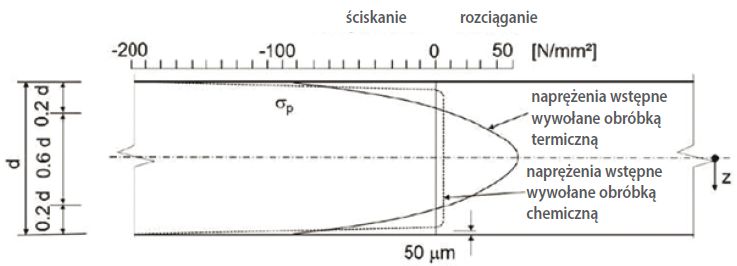
Rys. 2. Rozkład naprężeń wewnętrznych w szkle, w którym wywołano naprężenia wstępne w procesie obróbki termicznej oraz chemicznej.
(...)
(...)
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2017, która odbyła się w dniach 28-30 czerwca 2017 r. w Tampere w Finlandii
Jürgen Neugebauer
Uniwersytet Nauk Stosowanych, Wyższa Szkoła Zawodowa Joanneum
Irma Kasumovic
Ośrodek Badawczo-Rozwojowy im. Josefa Ressela
Ivo Blazevic
Ośrodek Badawczo-Rozwojowy im. Josefa Ressela
Bibliografia
[1] EN 12150 Szkło w budownictwie. Termicznie hartowane bezpieczne szkło sodowo-wapniowo-krzemianowe.
[2] EN 1863 Szkło w budownictwie. Termicznie wzmocnione szkło sodowo-wapniowo-krzemianowe.
[3] EN 12337 Szkło w budownictwie. Chemicznie wzmocnione szkło sodowo-wapniowo-krzemianowe.
[4] Neugebauer J.: Movable canopy, Materiały konferencyjne, Glass Performance Days, Tampere,
Finlandia, 2015.
[5] Neugebauer J.: Investigation of different test set scenarios for determination of ultimate bendig
stress of thin glass. Materiały konferencyjne; Engineered Transparenty, Glasstec, Dusseldorf, 2016.
[6] Illguth M., Schulera C., Bucak Ö.: The effect of optical anisotropies on building glass façades
and its measurement methods. Frontiers of Architectural Research 4; 119–126; Elsevier; 2015.
[7] Schula S.: Charakterisierung der Kratzanfälligkeit von Gläsern im Bauwesen, praca doktorska;
Darmstadt; 2014.
[8] Gross D., Seelig T.: Bruchmechanik. Wydawnictwo Springer-Verlag Berlin Heidelberg; 2011.
[9] EN 1288-2 Szkło w budownictwie. Określanie wytrzymałości szkła na zginanie. Część 2: Metoda
współosiowego dwupierścieniowego badania płaskich próbek o dużych powierzchniach
badanych.
[10] EN 1288-3 Szkło w budownictwie. Określenie wytrzymałości szkła na zginanie. Część 3: Badanie na próbkach podpartych na dwóch podporach (czteropunktowe zginanie).

Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 6/2019