W pierwszej części artykułu przedstawiono model matematyczny do obliczania obciążenia szyb, z uwzględnieniem współpracy warstwy gazowej zamkniętej w szczelnej komorze szyby zespolonej. Poniżej przedstawiono przykłady wykorzystania modelu do praktycznych analiz.
W tekście występują odwołania do wzorów i tabeli z części pierwszej, gdzie znajdują się również opisy używanych oznaczeń. Również numeracja rysunków jest kontynuowana.
Wartość interakcji obciążenia powierzchniowego jednej z szyb zestawu
Jak opisano wcześniej w obciążonej szybie zespolonej zachodzi sprzężenie gazowe obciążeń. Liczbowo wyraża się ono zmianą ciśnienia gazu Ap w komorze szyby obciążonej w odniesieniu do ciśnienia początkowego, przyjętego za poziom odniesienia.
Jest ono związane ze zmianami objętości i ciśnienia gazu w komorze szyby, spowodowanymi objętością pola przemieszczenia szyb ograniczających komorę.
Efektem sprzężenia gazowego jest interakcja międzyszy-bowa tzn. przekazywanie obciążeń miedzy szybami zestawu (rys. 8). Liczbowo interakcję pojedynczego obciążenia można opisać współczynnikiem interakcji Δp/q, który wskazuje, jaka część obciążenia q przekazywana jest z szyby obciążonej bezpośrednio, na szybę gazowo sprzężoną.
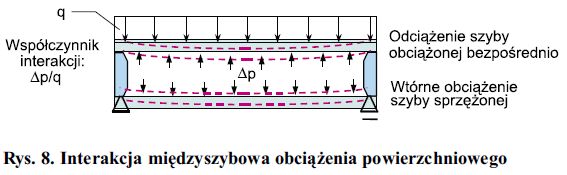
Rys. 8. Interakcja międzyszybowa obciążenia powierzchniowego
Zależność współczynnika interakcji Ap/q od szerokość szyby a wyznaczono analizując funkcję Δp/q = f(a). Funkcję tę określono na podstawie wzoru (14) i współczynników z tabeli 1.
Z uwagi na skomplikowaną postać rozwiązania analitycznego, podano je w formie graficznej na rys. 9.
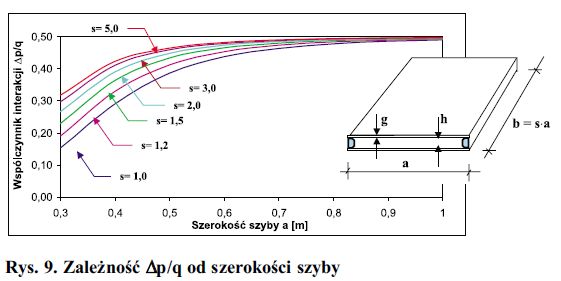
Rys. 9. Zależność Δp/q od szerokości szyby
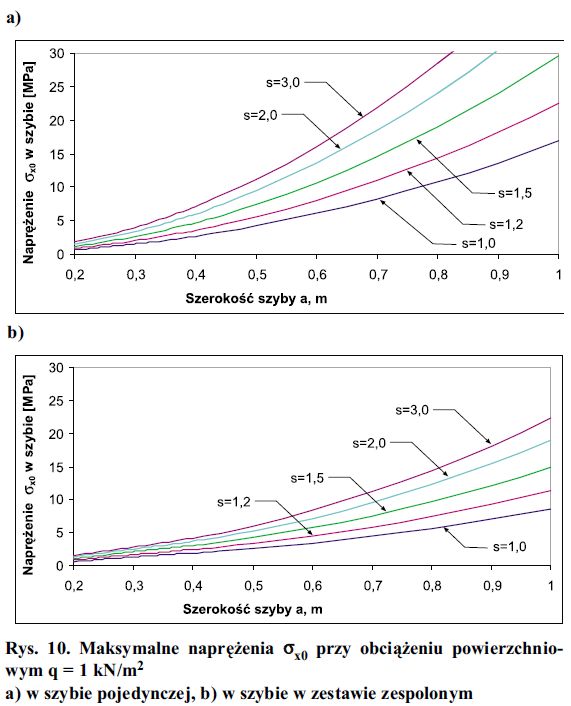
Rys. 10. Maksymalne naprężenia σx0 przy obciążeniu powierzchniowym q = 1 kN/m2
a) w szybie pojedynczej, b) w szybie w zestawie zespolonym
Przykład 1. Zbadać zależność współczynnika interakcji Ap/q od szerokości szyby.
Parametry zestawu: E = 70 GPa; v = 0,22; g = 0,004 m, grubość warstwy gazowej h = 0,016 m, p0 = 100 kPa.
Przyjęto obciążenie powierzchniowe jednej z szyb q = 1 kN/m2 oraz zmienny stosunek długości do szerokości szyby s.
Z wykresów na rys. 9 wynika, że wraz ze wzrostem wymiarów szyby współczynnik interakcji Δp/q dąży do 0,5. Oznacza to, że w przypadku szyb wielkowymiarowych obciążenia rozkładają się na obie szyby prawie po połowie. Jest to zjawisko korzystne, ponieważ dla szyb o dużych wymiarach następuje znaczna redukcja naprężeń, w wyniku zmniejszenia obciążenia działającego na pojedynczą szybę w zestawie.
Naprężenia w szybie oszacowano, przy znanym obciążeniu wypadkowym szyby, z klasycznej teorii płyt. Powyższą redukcję naprężeń pokazano na rys. 10.
Przykład 2. Zbadać zależność współczynnika interakcji obciążenia powierzchniowego szyby Δp/q od wybranych parametrów: wielkości obciążenia q, grubości szyb g, i ciśnienia początkowego p0.
Analizy dokonano dla zestawu o stosunku boków s = 2. Pozostałe dane przyjęto jak w przykładzie 1.
Zależność współczynnika interakcji Ap/q od wybranych parametrów wyznaczono analizując funkcje Δp/q = f(z) gdzie z, oznacza kolejny wpływ. Wykresy na rys. 11-13 obrazują graficznie odpowiednie funkcje. Funkcje te zbadano w zakresach charakterystycznych dla rzeczywistych szyb. Zwraca uwagę mała wrażliwość Δp/q na zmiany wartości obciążenia i ciśnienia początkowego gazu wewnątrz komory.
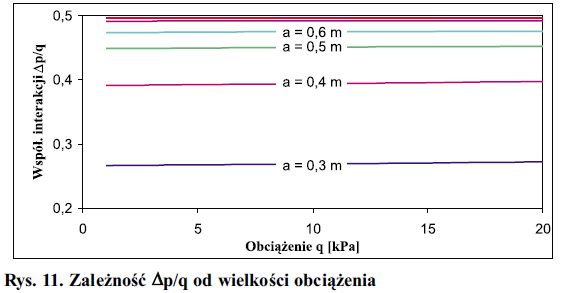
Rys. 11. Zależność Δp/q od wielkości obciążenia
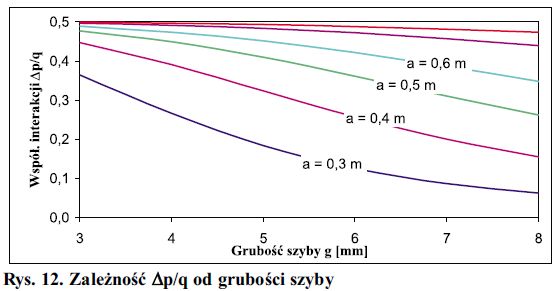
Rys. 12. Zależność Δp/q od grubości szyby
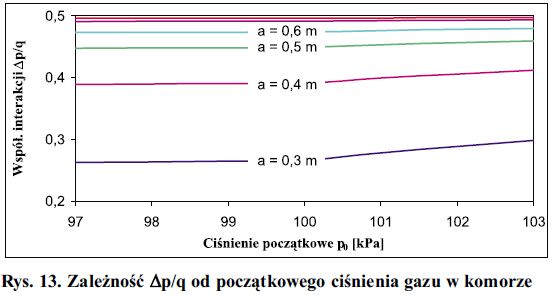
Rys. 13. Zależność Δp/q od początkowego ciśnienia gazu w komorze
Kompensacja zmian ciśnienia atmosferycznego ciśnieniem gazu w komorze
Poniżej przeanalizowano obciążenie szyby zmianami zewnętrznego ciśnienia atmosferycznego, przy pominięciu pozostałych wpływów. Gaz w szczelnej komorze szyby nieobciążonej posiada początkowe parametry ciśnienia p0, objętości v0 i temperatury T0. Zmiana zewnętrznego ciśnienia atmosferycznego do wartości pa powoduje powstanie zewnętrznego obciążenia obu szyb Δpa = pa - p0.
Objętość pola przemieszczenia tego obciążenia ma jednak wpływ na zmianę ciśnienia wewnątrz komory Δp (rys. 14). Zmiana ciśnienia gazu w komorze powoduje obciążenie obu szyb, skierowane przeciwnie do zmian ciśnienia zewnętrznego. Efektem sprzężenia gazowego jest więc w tym wypadku częściowa kompensacja zmian ciśnienia atmosferycznego. Współczynnik interakcji Δp/Δpa wskazuje, jaka część zmiany ciśnienia zewnętrznego Δpa została skompensowana zmianą ciśnienia gazu w komorze.
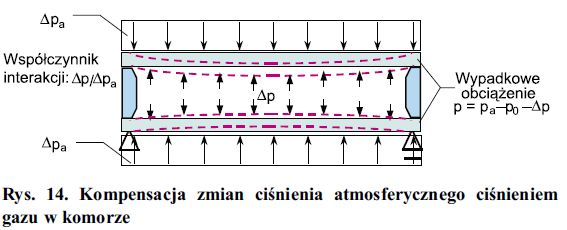
Rys. 14. Kompensacja zmian ciśnienia atmosferycznego ciśnieniem gazu w komorze
Przykład 3. Zbadać zależność współczynnika interakcji obciążenia zmianą ciśnienia atmosferycznego Δp/Δpa od szerokości szyby
Zależność Δp/Δpa na szerokość szyby a, przeanalizowano dla szyby zespolonej o parametrach, jak w przykładzie 1.
Przyjęto zmianę ciśnienia zewnętrznego Δpa = 5 kPa. Przeanalizowano funkcję Δp/Apa = f(a) przy wykorzystaniu wzoru (12). Wyniki analizy przedstawiono na rys. 15.
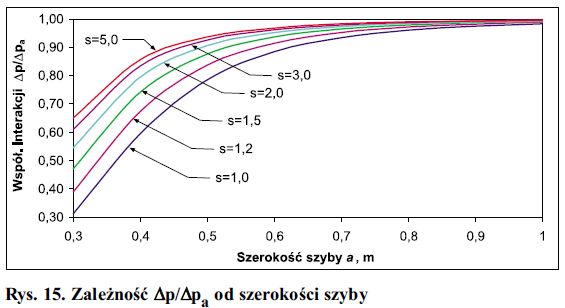
Rys. 15. Zależność Δp/Δpa od szerokości szyby
Wielkość Δp/Δpa jest miarą kompensacji skutków zmian ciśnienia atmosferycznego ciśnieniem gazu w komorze. Przy zwiększaniu wymiarów zestawu Δp/Δpa dąży do 1, tzn. obciążenie szyb zanika. Można udowodnić, że przy danych parametrach zestawu Δp/Δpa jest dwukrotnie większe niż współczynnik interakcji obciążenia powierzchniowego Δp/q.
Ponieważ dla dużych rozmiarów szyb obciążenia zanikają, przy rozpatrywaniu naprężeń w szybie należy zwrócić uwagę, że dla każdego zestawu istnieje szerokość krawędzi, przy której naprężenia przy zmianie ciśnienia zewnętrznego są maksymalne. Naprężenie te, wyznaczone na podstawie klasycznej teorii płyt pokazano to na rys. 16.
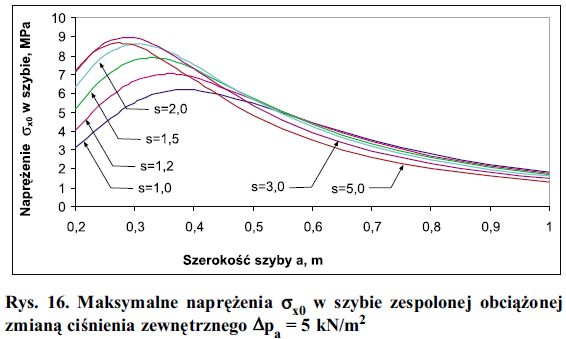
Rys. 16. Maksymalne naprężenia σx0 w szybie zespolonej obciążonej zmianą ciśnienia zewnętrznego Δpa = 5 kN/m2
Naprężenia temperaturowe w szybach zespolonych
Przy rozpatrywaniu obciążeń termicznych w szybach zespolonych należy mieć na uwadze:
- naprężenia wynikające z nierównomiernego ogrzania powierzchni szyby,
- naprężenia wynikające ze zmiany temperatury gazu w komorze,
- naprężenia spowodowane liniowymi w grubości szyby zmianami temperatury.
Pierwszy w wymienionych czynników nie jest związany ze sprzężeniem gazowym. Chodzi tutaj o naprężenia powstałe na granicy światło-cień, w przypadku gdy na część szyby padają promienie słoneczne, a część jest przed nimi osłonięta (np. ramą okienną, sąsiednim budynkiem).
Przyjmuje się, że naprężenia termiczne z tym związane mogą być niebezpieczne dla szkła, przy następujących różnicach temperatur:
- 30-40 K dla szkła zwykłego,
- 100 K dla szkła półhartowanego,
- 150 K dla szkła hartowanego.
Zmiana temperatury gazu w komorze ΔT, zgodnie z prawem gazowym (1), wywołuje zmianę jego ciśnienia Δp i objętości komory Δv. Zmiana ciśnienia Δp stanowi obciążenie szyby. Należy zwrócić uwagę, że obciążenie to jest charakterystyczne dla komór szczelnych, w przypadku szyby zdehermetyzowanej ciśnienie komorowe wyrównuje się z atmosferycznym i powyższe obciążenie nie występuje.
Przykład 4. Oszacować naprężenia związane ze zmianą temperatury gazu w komorze.
Przyjęto szybę zespoloną o następujących parametrach: grubość szkła g = 4 mm, sztywność szyby D = 0,4595 kNm, grubość komory h = 16 mm, parametry początkowe gazu p0 = 100 kPa, T0 = 290 K. Obliczono maksymalne naprężenie σx0 w szybach zestawu, spowodowane zmianą temperatury gazu do Tk = 310 K.
Przy rozpatrywaniu zmiany ciśnienia gazu w komorze uwzględniono zmiany objętości komory tzn. objętość pola przemieszczenia obciążonych szyb. Przy obliczaniu obciążenia Δp korzystano ze wzoru (11). Wyniki obliczeń przedstawiono na rys. 17.
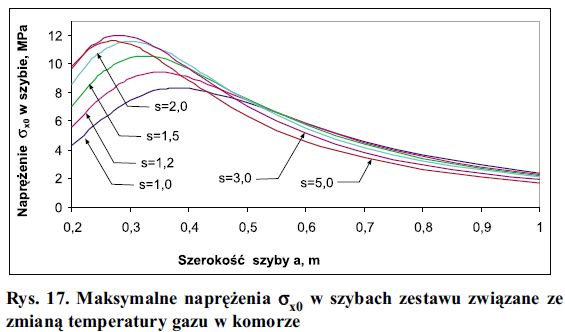
Rys. 17. Maksymalne naprężenia σx0 w szybach zestawu związane ze zmianą temperatury gazu w komorze
Podobnie jak w przypadku obciążenia zmianą ciśnienia zewnętrznego, dla każdej szyby istnieje szerokość, dla której naprężenia w szybie są maksymalne. Wynika to z faktu, że w miarę wzrostu wymiarów szyby zmiany ciśnienia komorowego są kompensowane zmianami objętości komory, wywołanymi objętością pola przemieszczenia, przez co radykalnie zmniejsza się wartość Δp. Np. dla s = 2: Δp = 1,653 kN/m2 przy a = 0,4 m; Δp = 0,0561 kN/m2 przy a = 1 m.
Można udowodnić, że przy danych parametrach zestawu szerokość, przy której występują maksymalne naprężenia, jest taka sama przy obciążeniu zmianą temperatury gazu, jak przy obciążeniu zmianą ciśnienia zewnętrznego.
Szyba obciążona liniowymi w swojej grubości zmianami temperatury, w przypadku komory nieszczelnej i swobodnego połączenia z oramowaniem, doznaje beznaprężenio-wego przemieszczenia. W przypadku komory szczelnej (rys. 18) objętość pola przemieszczenia od tego obciążenia wpływa na zmianę ciśnienia gazu w komorze.
Zmiana ta, Δp, stanowi jednoczesne obciążenie obu szyb zestawu, bez względu na to, na której szybie występują różnice temperatur powierzchniowych. Podobnie jak przy zmianie temperatury gazu w komorze, obciążenie to jest charakterystyczne dla komór szczelnych i nie występuje w przypadku dehermetyzacji komory.
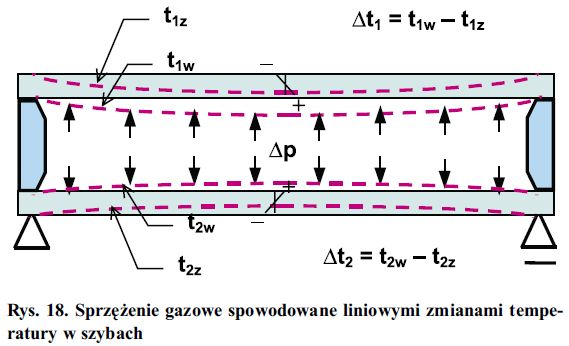
Rys. 18. Sprzężenie gazowe spowodowane liniowymi zmianami temperatury w szybach
Przykład 5. Oszacować naprężenia związane z różnicą temperatur na powierzchni szyb zestawu.
Na rys. 19 przedstawiono wyniki obliczeń maksymalnego naprężenia w szybach obciążonych różnicą temperatur powierzchniowych, w sumie na obu szybach ΣΔt = 37oC. W obliczeniach założono: sztywność szyb D = 0,4516 kNm, współczynnik Poissona v = 0,22; współczynnik rozszerzalności liniowej szkła β = 9-10-6 1/K i początkowe ciśnienie gazu p0 = 100 kPa. Do obliczenia obciążenia Δp korzystano ze wzoru (18).
Z wykresów na rys. 19 wynika, że przy wzroście wymiarów szyb naprężenia w szybach rosną tylko do pewnej granicznej wartości.
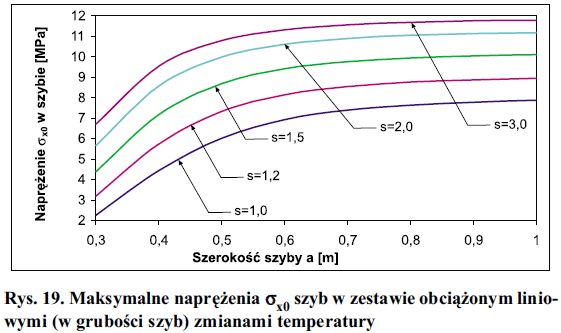
Rys. 19. Maksymalne naprężenia σx0 szyb w zestawie obciążonym liniowymi (w grubości szyb) zmianami temperatury
Wnioski
1. Pod wpływem działających na szybę zespoloną obciążeń klimatycznych, związanych ze zmianami ciśnienia atmosferycznego i temperatury, następuje ugięcie szyb zestawu. Na podstawie ugięcia można oszacować zmianę objętości komory mierzoną objętością przemieszczenia szyb. Zmiana objętości wpływa na zmianę obciążenia każdej z szyb, wywołaną sprzężeniem gazowym obciążeń.
2. Wskutek istniejącej w szczelnej komorze międzyszybowej interakcji obciążeń, część obciążenia powierzchniowego działającego na jedną z szyb przekazywana jest na szybę gazowo sprzężoną.
3. Przy zwiększaniu wymiarów szyb lub przy zmniejszaniu grubości komory gazowej, przy założeniu jednakowych sztywności obu szyb, współczynnik interakcji obciążenia powierzchniowego dąży do 0,5. W takim przypadku obciążenia rozkładają się po połowie na obie szyby.
4. Po uwzględnieniu w programach obciążeń szyb zespolonych gazowego sprzężenia obciążeń, siły wewnętrzne, naprężenie i przemieszczenie w obciążonych szybach, można obliczać stosując metody klasycznej mechaniki konstrukcji.
5. Zmiany zewnętrznego ciśnienia atmosferycznego oraz temperatury gazu w komorze wywołują naprężenia w szybach zestawu. Przy wzroście wymiarów szyb naprężenia te początkowo rosną, osiągają maksimum, a następnie maleją dla szyb wielkowymiarowych.
6. Zróżnicowanie temperatur po grubości szyb wywołuje znaczące naprężenia, których nie można pominąć w analizie wytężenia szyb.
dr inż. Zbigniew Respondek
Politechnika Częstochowska
patrz też:
- Metoda projektowania szyb zespolonych , Artur Piekarczuk, Świat Szkla 3/2008
więcej informacji: Świat Szkla 1/2005































