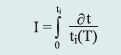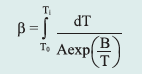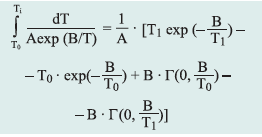Przebieg przemian fazowych zachodzących podczas ogrzewania NiS w świetle badań termicznych
Ze względu na charakterystyczne przejście metal α półprzewodnik w temperaturze 265 K, przeprowadzono wiele badań nad wysokotemperaturową fazą α-NiS. Nie występująca w naturze wysokotemperaturowa forma α-NiS, posiada heksagonalną strukturę fazy typu nikielinu NiAs i w warunkach otoczenia jest fazą metastabilną [1]. Przyjmuje się, że forma β-NiS ulega przemianie do formy α-NiS w temperaturze 390oC.
W zależności od metodologii badania według niektórych autorów przemiana ta następuje w temperaturze 400oC [2], czy też w temperaturze 397oC, przy ciśnieniu atmosferycznym [3]. Różnice w temperaturze przejścia formy α-NiS w formę β-NiS wynikają z różnych warunków ciśnienia podczas prowadzenia badań. Podawane niższe wartości temperatury przemiany fazowej NiS zostały zmierzone przy wzroście ciśnienia. Metodą, która pozwala w sposób precyzyjny wyznaczyć temperaturę przemiany fazowej, jak również zmiany właściwości NiS pod wpływem temperatury jest metoda termicznej analizy różnicowej.
Analiza termiczna DTA, TG/DTG czystego siarczku niklu
Przebieg przemian fazowych, zachodzących w trakcie ogrzewania NiS rejestrowano przy pomocy urządzenia Derivatograph-C (MOM Budapest). Do badań użyto wysokiej czystości siarczku niklu II (99,95%, o uziarnieniu 100 μm) firmy Johnson Mathey GmbH. Pomiary prowadzono w atmosferze powietrza. Próbkę NiS o masie 100 mg rozdrobniono, po czym umieszczono w tyglu ceramicznym i ogrzewano ze stałą szybkością grzania 10oC/min-1, od temperatury pokojowej do temperatury 1000oC.
Na podstawie otrzymanej krzywej DTA/TG/DTG określono temperaturę przemiany polimorficznej fazy siarczku niklu β -> α. Przemianie tej towarzyszył zarejestrowany na krzywej DTA efekt egzotermiczny. Jednocześnie na krzywej TG nie zaobserwowano zmiany masy, co może potwierdzać wystąpienie przemiany fazowej w temperaturze wynoszącej 376oC (rys. 1). Według danych literaturowych [3-5] β-NiS (milleryt) ulega transformacji do formy α-NiS w temperaturze 652 K (379oC).
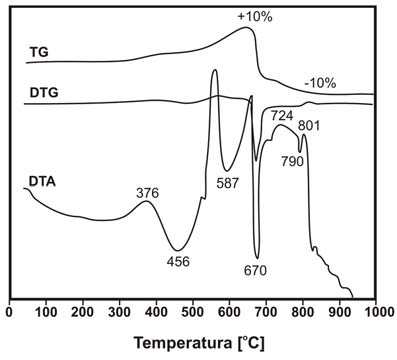
Rys. 1. Krzywa DTA,TG/DTG czystego chemicznie siarczku niklu
Pojawienie się na krzywej DTA efektu endotermicznego w przedziale temperatur 550-659oC z minimum w temperaturze 587oC, oraz obserwowany na krzywej TG przyrost masy świadczy o formowaniu się NiSO4 według reakcji opisanych przez Dunn’a i Kelly’ego [2]:
a) NiS +2O2 -> NiSO4 400-785oC
b) NiO+SO2+0.5 O2 -> NiSO4 500-785oC
c) NiS +1.5O2 -> NiO+SO2 540-552oC i 682-692oC
d) 3NiS + 2NiSO4 -> Ni3S2+2NiO+3SO2 682-692oC
e) 10NiS + 2O2 -> Ni7S6+ Ni3S2+2SO2 682-692oC
f) Ni7S6+9.5O2 -> 7NiO+6SO2 682-780oC
Ni7S6+12.5O2 -> 6NiSO4 +NiO
g) Ni3S2(s) -> Ni3S2(l) 793oC
h) Ni3S2(l)+ 3.5O2 3NiO+2SO2 793oC
i) NiSO4 -> NiO+SO2+0.5 O2 >800
Na podstawie zarejestrowanych krzywych DTA/ TG/DTG, w zakresie temperatur 460-700oC, zaobserwowano całkowite utlenienie siarczku niklu z formowaniem się siarczanu niklu NiSO4, heazlewoodytu Ni3S2 i tlenku niklu NiO. Najnowsze badania prowadzone przez Strabaca i in. [6] nad utlenianiem α-NiS dla zakresu temperatur 670-700oC opisują trójstopniowy mechanizm procesu utleniania:
1) proces utleniania α-NiS do NiO, zachodzący w temperaturach 943-953 K (670-680oC);
2) proces utleniania α-NiS do Ni3S2 w temperaturze 973 K (700oC);
3) utlenianie Ni3S2 do NiO w temperaturze powyżej 973 K (>700oC).
Według Strabaca i in. proces utleniania NiS zachodzi w przedziale temperatur od 873 do 973 K (600-700oC), towarzyszy temu silny efekt egzotermiczny z maksimum w temperaturze 629oC oraz wyraźny przyrost masy na krzywej TG. Proces utleniania siarczku niklu może przebiegać zgodnie z reakcją:
2NiS + 7/2 O2 -> NiSO4 + NiO + SO2
Proces rozpadu NiSO4 rozpoczyna się w temperaturze 700oC, jest on widoczny jako efekt endotermiczny z wyraźnym minimum w temperaturze 849oC na krzywej DTA oraz jako znaczący spadek masy próbki na krzywej TG. Proces rozpadu NiSO4 może przebiegać zgodnie z reakcją:
NiSO4 -> NiO + SO2 + 1/2 O2
Przeprowadzona analiza DTA-TG-DTG czystego siarczku niklu wykazała, że w pierwszej kolejności β-NiS ulega transformacji do α-NiS. Następnie rozpoczyna się proces utleniania NiS do NiSO4 i NiO. W wyższych temperaturach następuje rozpad NiSO4. Końcowym produktem utleniania jest NiO.
Krystalizacja siarczku niklu NiS
W celu oszacowania czasu pękania hartowanych wyrobów szklanych kinetykę rekrystalizacji αβ NiS badano wykorzystując termoanalizator DSC-7 firmy Perkin Elmer. Pomiary prowadzono w warunkach izo- i nieizotermicznych. Do badań użyto wysokiej czystości siarczku niklu II (99,95%, o uziarnieniu 100 μm) firmy Johnson Mathey GmbH. Próbki α-NiS (w temperaturach otoczenia) otrzymano poprzez ogrzewanie β-NiS do 450ºC w piecyku DSC, przetrzymywanie ich w tej temperaturze przez 10 min, a następnie gwałtowne schłodzenie sprężonym powietrzem. Proces prowadzono w atmosferze azotu. Celem potwierdzenia rodzaju otrzymanej fazy krystalicznej α-NiS wykonano badania XRD (rys. 2).

Rys. 2. Dyfraktogram α-NiS otrzymany poprzez ogrzewanie β-NiS do 450oC w piecyku DSC
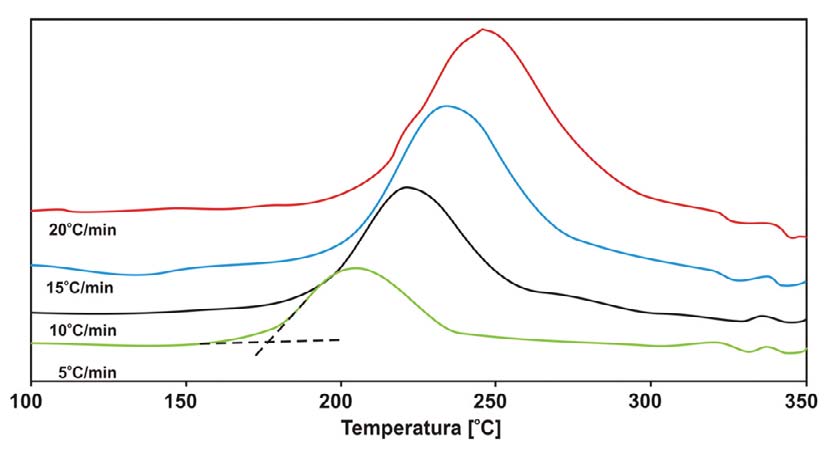
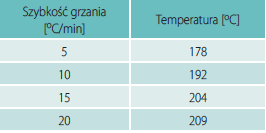
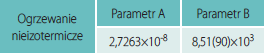
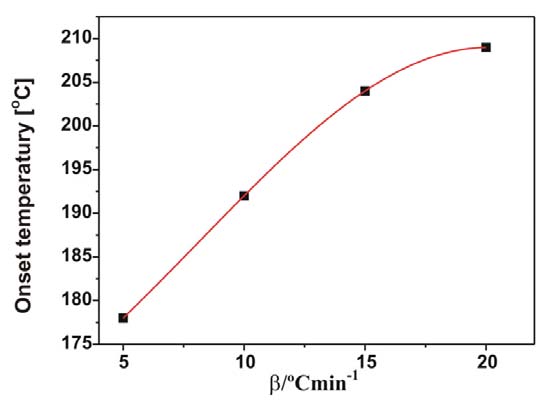
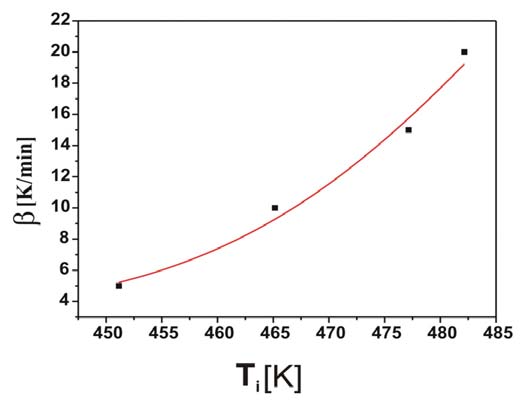
Przy pomiarach nieizotermicznych stosowano prędkości ogrzewania wynoszące: 5, 10, 15, 20oC/min. Dla każdej prędkości wyznaczono oddzielną krzywą kalibracyjną używając indu jako wzorca. Próbki α-NiS zamknięto w aluminiowych tyglach i umieszczono w komorze próbek, jako próbki odniesienia użyto pustego tygla.
Pomiary izotermiczne prowadzono w temperaturach 130, 140, 150oC. Temperatury krystalizacji izotermicznej osiągnięto przez ogrzewanie próbki α-NiS z prędkością 10oC/min zaczynając od temperatury pokojowej.
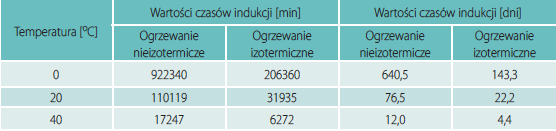
Wyznaczenie okresu indukcji za pomocą grzania izotermicznego
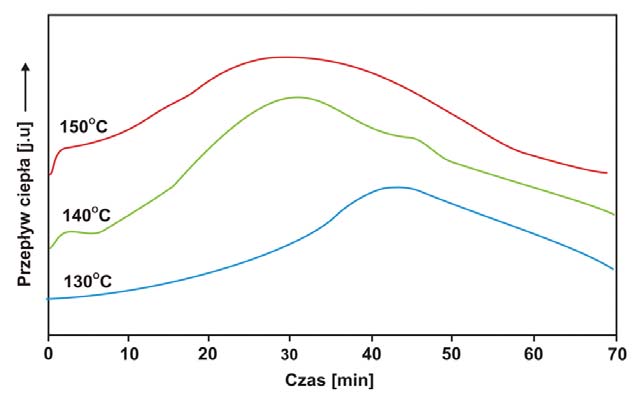
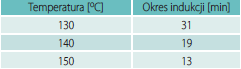
Izotermiczne krzywe DSC dla rekrystalizacji α β- NiS przedstawiono na rys. 3 Okresy indukcji dla rekrystalizacji izotermicznej wyznaczono z przegięć krzywych DSC (Tab. 1). Okres indukcji wykazuje silną zależność od temperatury, co można wyrazić w formie wykładniczej [7]:
![]()
gdzie:
ti – czas indukcji, A i B – stałe, T – temp. bezwzględna
(...)
Sebastian Bielecki
Państwowa Wyższa Szkoła Zawodowa
w Tarnowie, Zakład Technologii Materiałów
Manuela Reben
AGH Akademia Górniczo-Hutnicza im.
Stanisława Staszica w Krakowie, Katedra
Technologii Szkła i Powłok Amorficznych
Spis literatury cytowanej
[1] Bolewski A.: Mineralogia Szczegółowa, Wydawnictwa Geologiczne, 1982.
[2] Dunn J.G., Kelly C.E.: J. Thermal Anal. vol. 12, 43-52, 1977.
[3] Kullerud G, Yund R.A., I.: Petrology, vol. 3, part 1, 126- 175, 1962.
[4] Ballantyne E.R., CSIRO Div. Bldg. Res., Rep 061, Melbourne 1961.
[5] Swain M.V., J. Mat. Science 16, 151-158, 1981.
[6] Strabac N., et al., J. Serb. Chem. Soc., 73(2), 211-219, 2008.
[7] Isaev A.I., Deng J.S., Rubber Chem. Technol., 61, 343, 1987.
[8] Simon P., Kucma A.: J. Therm. Anal. Cal., 56, 1107, 1999.
patrz też:
- Inkluzje siarczku niklu jako wada szkła hartowanego Część 3 , Manuela Reben, Sebastian Bielecki, Świat Szkła 2/2016
- Inkluzje siarczku niklu jako wada szkła hartowanego Część 2 , Manuela Reben, Sebastian Bielecki, Świat Szkła 1/2015
- Inkluzje siarczku niklu jako wada szkła hartowanego Część 1 , Manuela Reben, Sebastian Bielecki, Świat Szkła 5/2014
- Wady szkła na fasadach Część 1 Szkło hartowane i warstwowe, Anna Balon-Wróbel, Agnieszka Marczewska, Świat Szkła 3/2012
- Oszklenia bezpieczne w budownictwie , Tadeusz Tarczoń, Świat Szkła 10/2010
- Inkluzje siarczku niklu w szkle , M. Reben, J. Wasylak, M. Szumiński, S. Bielecki, Świat Szkła 1/2010
- Poprawa właściwości fizykochemicznych szkła float, Marcin Drajewicz , Jan Wasylak, Świat Szkła 12/2008
- Zmiana budowy wewnętrznej szkła – hartowanie i odprężanie, Marcin Drajewicz, Manuela Reben, Katarzyna Cholewa-Kowalska, Świat Szkła 6/2007
- Uszlachetnianie powierzchni szkła , Jan Wasylak, Marcin Drajewicz, Świat Szkła 12/2006
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 02/2016