W artykule przedstawiono model analityczny, który umożliwia obliczenie przyrostu naprężeń i maksymalnej wytrzymałości belki ze szkła laminowanego z uwzględnieniem wielowarstwowego systemu laminacji, pozwalającego na ograniczone prognozowanie,  przesuwanie względem siebie elastycznych warstw poddanych naprężeniom ścinającym. Model ten może być zastosowany do laminatów o dowolnym kształcie i wielkości, poddanych głównie jednoosiowemu zginaniu.

Nie przyjęto żadnych specyficznych założeń upraszczających przy formułowaniu procedur, więc niedokładności modelowania są marginalne, czego dowodem są porównania obliczeń (prognoz) według teoretycznego modelu z wynikami badań doświadczalnych.

Wstęp
Szkło laminowane (LG) składa się najczęściej z dwóch warstw szkła float i jednej warstwy pośredniej materiału termoplastycznego (elastomer), trwale połączonych ze sobą w autoklawie w wyniku działania wysokiego ciśnienia i temperatury. Obecnie elastomerowa warstwa wykonywana jest z głównie z PVB (polywinylobutyral). Zginanie szkła laminowanego jest przedmiotem tego opracowania.

Wszystkie opisy zachowań szkła laminowanego, pojawiające się w opublikowanych artykułach, rozpoczynały się od subiektywnej oceny, że rzeczywiste zachowanie się struktury szkła laminowanego leży między dwoma intuicyjnie przewidywalnymi granicznymi przypadkami: warstwowym i monolitycznym.

Podejmowane są próby ustalenia granic nośności (wytrzymałości), obejmujące zarówno metody doświadczalne jak też numeryczne (analityczne). Jednak pierwsze próby polegały na usiłowaniu opisania podziału obciążenia i przekazywania naprężeń ścinających między szkłem i folią laminującą (PVB) przez rodzaj współczynnika, który z góry określi stosunek procentowy między maksymalnymi naprężeniami głównymi rozciągającymi w systemie szkła monolitycznego z porównywalnym systemem warstwowym.

Próby te zostały podważone, ponieważ są znaczne różnice między zachowaniem przekładki z folii PVB a płytami szkła. Stąd wzięła się potrzeba opracowania podejścia analitycznego, które rozpozna zdolność PVB do przeniesienia naprężeń ścinających między płytami szkła.

Model analityczny
Model ten dotyczy belek ze szkła laminowanego poddanych jednoosiowemu zginaniu, z osią zginania w płaszczyźnie przekładki PVB. Przewiduje on wzrost naprężeń i określa maksymalną wytrzymałość belki ze szkła laminowanego z daną geometrią, z modułem sprężystości dla szkła Eg i modułem sprężystości postaciowej GPVB dla PVB.

Wytrzymałość (nośność) – jak określono w normach – odnosi się do zauważenia pierwszego pęknięcia w płycie szklanej i nie rozważa się nośności struktury popękanego szkła.

W celu określenia maksymalnego obciążenia, model ten stosuje więc obliczeniową wartość wytrzymałości szkła na rozciąganie fgd. Przedmiotem modelu jest swobodnie podparta belka ze szkła laminowanego o długości L (rys. 1).

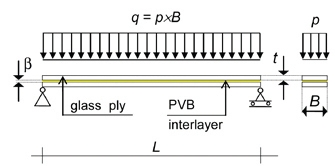
Rys. 1. Belka wykonana ze szkła float laminowanego przez sklejenie za pomocą przekładek z PVC. Przekrój podłużny z lewej, przekrój poprzeczny z prawej

Belka ze szkła laminowanego ma prostokątny przekrój, i składa się z dwóch warstw szkła, z których każda ma grubość i szerokość B oraz warstwy PVB o grubości β (beta) i szerokości B. W związku z tym szerokość belki LG jest B, a całkowita wysokość belki LG (głębokość) jest równa 2 x t + β , podczas gdy całkowita grubość szkła jest 2 x t. Równomiernie rozłożone boczne obciążenie o wielkości p działa wzdłuż całej powierzchni belki B x L.

Model zakłada że obciążenie liniowe o wielkości q = p x B działa równomiernie na całej długości L (rys. 2).

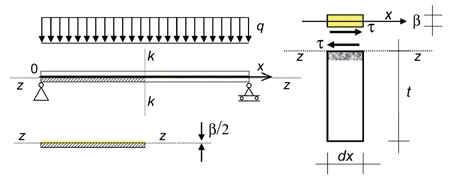
Rys. 2. Obliczenia można wykonać dla ¼ belki LG zamiast dla całej struktury. Matematyczna analiza zapewnia, że do obliczeń wystarczy: zacieniona ¼ część przekroju (po lewej stronie) jak też nieskończenie mały element wydzielony z tej zacienionej części (po prawej stronie) – zawierający odpowiednio połączone elementy PVB i szkła, z ich strefą połączenia (wzajemnego oddziaływania).

Folia PVB wydzielona z belki ze szkła laminowanego LG: siła ścinająca rozłożona na jednostkę powierzchni τi przekładki polimerowej z PVB, maksymalna wartość naprężeń τimax jest w x = 0. Rysunek pokazuje również odkształcenia przekładki ξ. Pozycje wzdłuż rozpiętości belki są identyfikowane przez oś X, która jest zbieżna z osią symetrii belki LG (rys. 2). Podpora przesuwna na końcu belki doświadczalnej zapewnia przyłożenie obciążeń, jak w membranie.

Model ten opiera się na następujących założeniach.
Powierzchnia przekroju każdej warstwy szkła jest prostopadła do osi wzdłużnej warstwy szkła przed zginaniem i pozostaje prostopadła do tej osi w czasie zginania. Szkło jest modelowane w zakresie liniowo-sprężystym z modułem Younga Eg = 70 000 N/mm2 oraz PVB w zakresie liniowo-sprężystym z modułem sprężystości postaciowej GPVB, który zależy od temperatury i czasu trwania obciążenia. Naprężenia rozciągające σ (sigma) w warstwie PVB są znikome w porównaniu do naprężeń σ (sigma) w warstwach szkła. Przekładka PVB przenosi naprężenia ścinające w nieistotnej wielkości w porównaniu do płyt szklanych.

Z powyższych hipotez wynikają następujące konsekwencje: mogą być spełnione wymagania odnośnie symetrii.

Strukturalne zachowanie belki LG jest symetryczne w odniesieniu do środka rozpiętości belki, również jako cała belka. Sama przekładka PVB jest asymetryczna do osi belki (osi x na rys. 2).

Szklane płyty przenoszą całkowitą wartość powstałego momentu zginającego (rys. 6) poprzez połączenie indywidualnego przenoszenia siły osiowej w każdej szklanej płycie N_t (siła osiowa w warstwie) i momentu zginającego w każdej szklanej płycie M_t (moment zginający w warstwie).

Stąd można zobaczyć odkształcenia  w przekroju szkła warstwowego jako posiadające dwa komponenty (elementy), jeden w wyniku działania N_t, oznaczone jako ε_N, a drugi powstały ze względu na M_t, oznaczony jako ε_M.

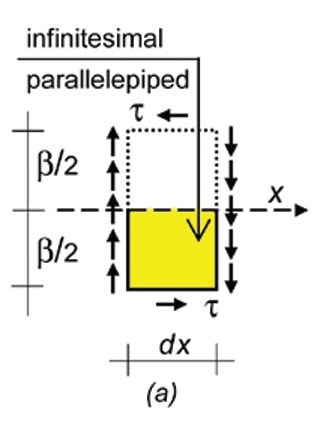
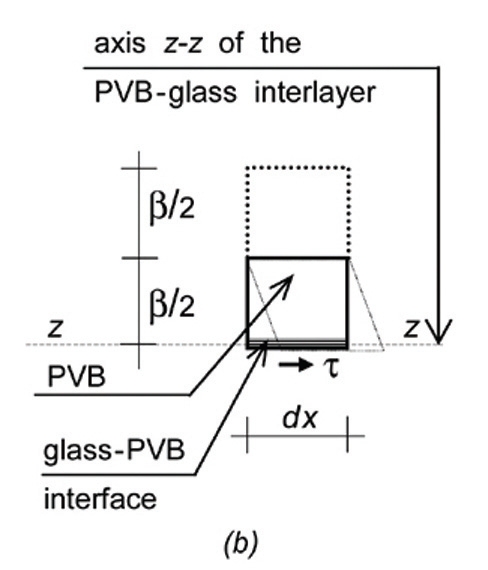
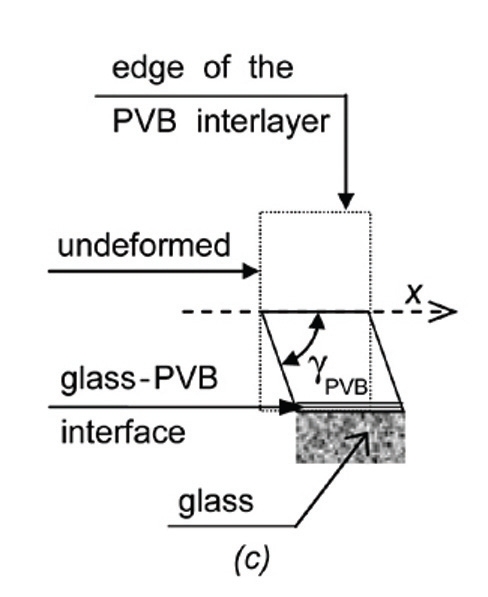
Rys. 3. Odkształcenia pierwszego rzędu – nieskończenie małego elementu PVB: (a) rozkład naprężeń ścinających na całej grubości folii PVB, (b) przesunięcie równoległościenne wykazuje odkształcenie wywołane ścinaniem i nieznaczące deformacje wywołane zginaniem, (c) elastyczne zachowanie elementu PVB: odkształcenie od naprężeń ścinających γ_PVB

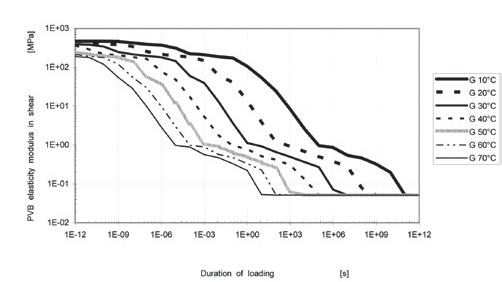
Rys. 4. Moduł sprężystości postaciowej G_PVB, dla folii PVB [N/mm²] wyznaczony doświadczalnie, w zależności od czasu trwania obciążenia [s] i temperatury [°C].

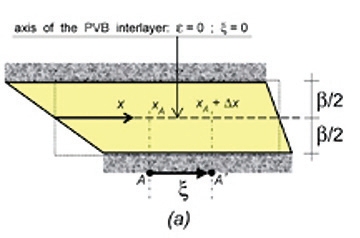
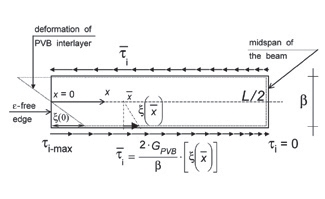
Rys. 5. Przekrój wzdłużny elementu folii PVB, pokazujący także wewnętrzne krawędzie płyt szklanych.

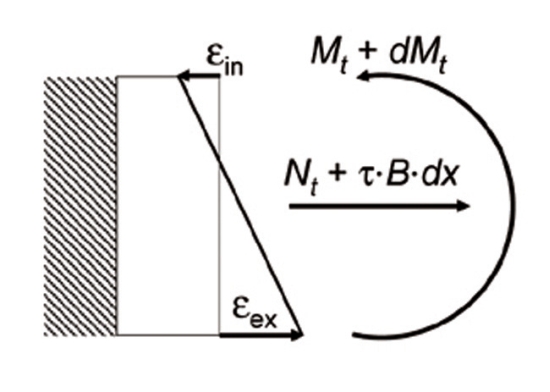
Fot. 6 (a). Rozkład odkształceń ε powstałych w wyniku zginania (na grubości jednej warstwy szkła).
Zakres odkształceń od ε_ex (materiał rozciągany) do ε_in (materiał ściskany), odkształcenie ε_in ma zwykle wartość ujemną i przedstawia skurcz materiału pod wpływem naprężeń ściskających, ale może mieć też niekiedy wartość dodatnią – gdy w całym przekroju panują naprężenia rozciągające.

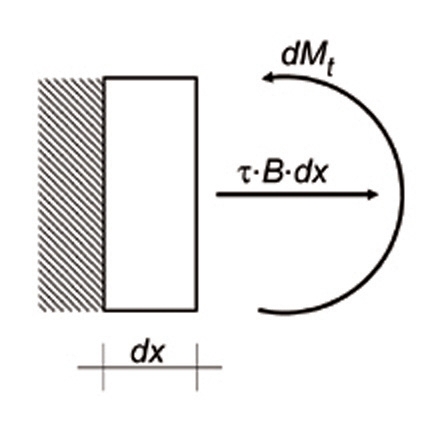
Fot. 6 (b). Obciążenie wywołane różnicą siły osiowej z lewej do prawej strony nieskończenie małego elementu dx – moment zginający dM_t

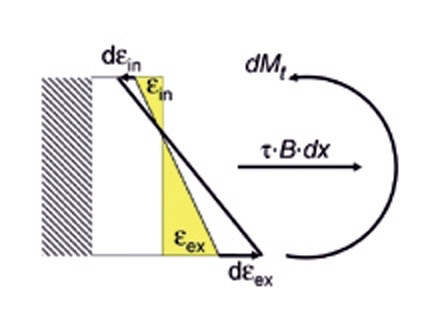
Fot. 6 (c). Różnica naprężeń wywołana przez różnicę prezentowanych oddziaływań wewnętrznych.

Rozważmy górną krawędź dolnej szklanej płyty, tj. dół połączenia PVB-szkło (oś Z-Z z rys. 2). Oznaczamy ξ poziome przemieszczenie tej krawędzi w stosunku do osi belki LG (rys. 5a). Ponieważ ta ostatnia nie jest transponowana, ξ jest całkowitym przemieszczeniem.

εin oznacza wydłużenie względne w kierunku x na tej krawędzi. Rozważmy zależność εin od zmiany pozycji elementu dx. Ponieważ dNt = τi ⋅B ⋅ dx, a pierwszą przestrzenną pochodną ξ jest εin, można wyprowadzić następującą zależność:

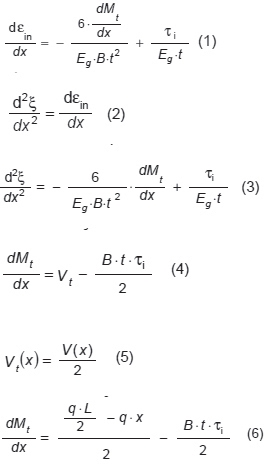
Wyliczając równanie (3) w zależności od q, algebraiczne przekształcenia prowadzą do następującego równania różniczkowego:

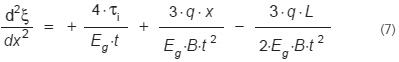
Związek pomiędzy ξ a odkształceniem PVB przy ścinaniu (pod wpływem naprężeń ścinających) γPVB prowadzi do następującego wzoru:

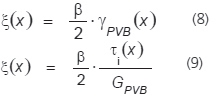
Wyrażając równanie (9) w zależności od τi jako funkcję od ξ, możemy podstawić τi w (7): 

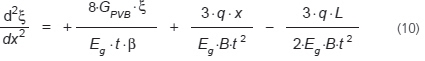
Ponieważ tylko ξ i x są zmienne, kanoniczna postać równania (10) jest następująca:

w którym stałe Φ, Ψ i Ω są zdefiniowane jako

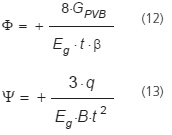
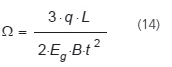
Ogólne i szczególne rozwiązania są następujące:

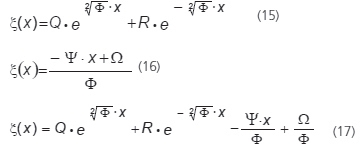
Dwa warunki brzegowe tego problemu są następujące:
(1) Podpory (rolki i zawiasy) powodują, że podłużne odkształcenie jest zerowe przy x = 0.
(2) Na środku rozpiętości belki mamy ξ (L / 2) = 0

Przyjmując warunek, że pierwsza pochodna (17) jest równa zeru dla x = 0, zgodnie z pierwszym warunkiem brzegowym (przypomnijmy, że Φ≠0) oraz przyjmując warunek, że (17) jest równa zeru dla x = L / 2, zgodnie z drugim warunkiem brzegowym, mamy:

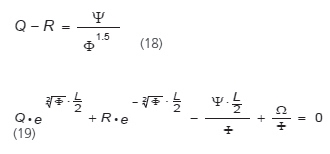
Warunki brzegowe prowadzą do zestawu dwóch równań liniowych i pozwalają na obliczenie (znalezienie) dwóch niewiadomych Q i R:

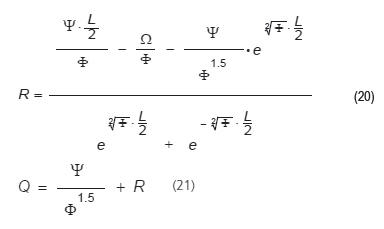
Wewnętrzne siły oddziaływania Nt i Mt są związane z q i τi (rys. 8):

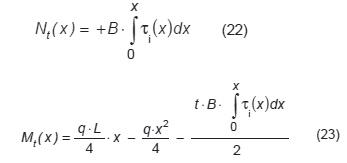
Gdy przekształcimy (23) z warunkiem, że warstwa działania gięcia leży na dolnej granicy Mt0 

oraz odkształcenie zachowuje warunek swobodnego przesuwu płyt, to

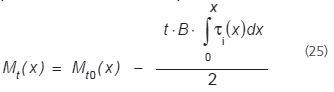
Maksymalne naprężenie w przekroju belki LG występuje przy dolnej krawędzi dolnej tafli szklanej. Takie naprężenia, oznaczone jako σex (x), są określone przez (22) i (25).

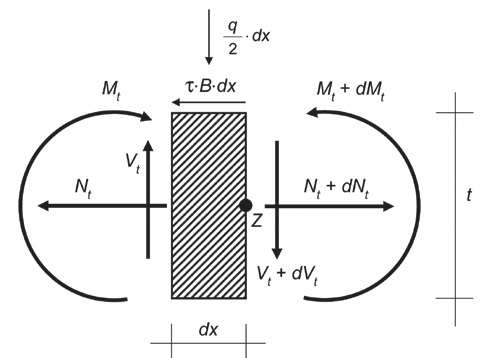
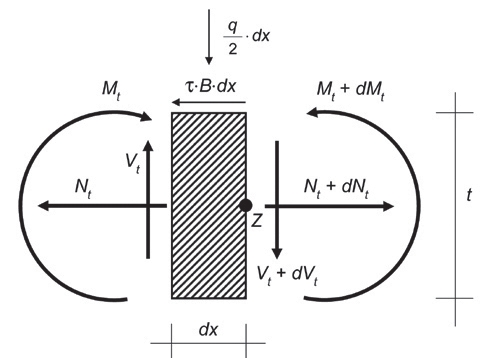
Rys. 7. Obciążenia zewnętrzne (cienka linia) i oddziaływania wewnętrzne (gruba linia) działające na nieskończenie mały element szkła warstwowego pokazano na rysunku 7. Punkt Z jest punktem równowagi obrotowej

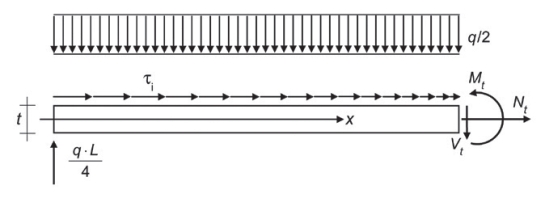
Rys. 8. Element o określonej długości wycięty z dolnej płyty szklanej z belki LG, z dodanymi odpowiednimi oddziaływaniami zewnętrznymi (q / 2, τi, q ⋅ L / 4) i wewnętrznymi (Mt, Nt, Vt).

Bezpieczeństwo konstrukcyjne belki LG jest mierzone poprzez porównanie naprężeń rozciągających σex z fgd, tj. przez sprawdzenie (27):

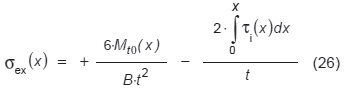
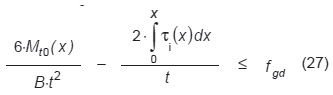
Spróbujmy określić ekwiwalentną (równoważną) wytrzymałość szkła f’gd. Równanie (27) może być przekształcone do postaci (29).

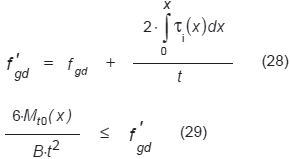
Belka LG przeniesie obciążenie q tylko wtedy, gdy (30) jest przestrzegane. Maksymalna wartość obciążenia jest taka, dla której σex = f ‘gd na środku rozpiętości (31):

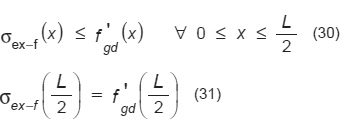
Analiza belki LG w skali produkcyjnej

Badania przeprowadzone na szeroką skalę w ramach analizy, której celem było zdobycie doświadczeń dla racjonalnego projektowania belek ze szkła laminowanego LG. Główne wyniki analizy są zilustrowane przez trzy przypadki ujęte w tab. 1).

Tabela 1. Odchyłki naprężeń σex i σin, przy obciążeniu qud i środku rozpiętości, w przypadkach A, B i C.

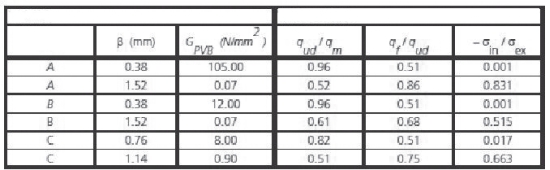
Pierwsza struktura (przypadek A) to prostokątna, dwustronnie podparta płyta, która przenosi jednolite obciążenie ciągłe p działające prostopadle do powierzchni środkowej płyty. Wymiary analizowanej płyty to L=3000 mm x B=1500 mm. Grubość każdej warstwy szkła t=12 mm, ogólnie określona grubość z laminowaniem to 12 + β (beta) + 12 mm. Wartość obliczeniowa wytrzymałości na rozciąganie szkła fgd = 19,0 N/mm2.

Druga struktura (przypadek B) to belka LG, w której warstwy szkła mają t = 8 mm oraz B = 610 mm. Belka jest obustronnie podparta, ma długość 5200 mm i jest poddawana obciążeniu równomiernie rozłożonemu, działającemu poprzecznie do powierzchni bocznej belki. W związku z tym całkowita grubość belki LG to 8 + β + 8 mm i szerokość B = 610 mm. Wartość obliczeniowa wytrzymałości na rozciąganie jest fgd = 48,0 N/mm2.

Trzecia struktura (przypadek C) to belka LG, w której szkło warstwowe ma po t = 4 mm oraz B = 250 mm. Belka jest swobodnie podparta, ma długość1800 mm i jest poddawana obciążeniu o równomiernym rozkładzie, działającemu poprzecznie do powierzchni bocznej. Grubość belki LG 4 + β + 4 mm i szerokość 250 mm. Wartość obliczeniowa wytrzymałości na rozciąganie jest fgd = 40,0 N/mm2.

Tabela 1 podaje główne wyniki w tych trzech przypadkach. Dane od 9 do 15 przedstawiają rozkład od krawędzi (x = 0) do środka rozpiętości (x = L / 2) dla reprezentatywnego naprężenie normalnego σ (sigma) działającego na włókna przy dolnej krawędzi z dolnej płyty szklanej, wraz z odpowiadającą wytrzymałością szkła.

Ponadto, na załączonych wykresach pokazano 4 rodzaje naprężeń:
- rzeczywiste naprężenie σex, oznaczone przez linię przerywaną;
- odpowiadającą mu wytrzymałość na rozciąganie f oznaczoną przez grubą linią ciągłą,

- naprężenie obliczone z „warstwowego” modelu analitycznego, w którym „założono” stan swobodnie przesuwnych płyt szkła, oznakowane jako σex-f i oznaczone przez linię kropek i kresek;

- naprężenie obliczone z „monolitycznego” modelu analitycznego, w którym „założono” stan dobrze sklejonych płyt szkła połączonych polimerem PVB, oznakowane jako σex-m i oznaczone przez cienką linię ciągłą.

Porównanie f’gd i σex-f pokazuje graficznie nierówność (29). Wtedy i tylko wtedy krzywa opisująca tę ostatnią funkcję leży poniżej pierwszej krzywej, gdy belka LG przenosi obciążenie. Jeśli dwie krzywe są styczne w środku rozpiętości, obciążenie działające odpowiada qud.

Obszar zawarty między krzywymi σex (x) i σex-f (x) obejmuje korzyści wynikające z uwzględnienia polimerowego sklejenia warstw szkła. Im bliżej σex do σex-f, tym odpowiednio mniejsza pozioma siła ścinająca na granicy szkło-folia PVB i odwrotnie.

Obszar zawarty w krzywej σex (x) i σex-M (x) wskazuje z kolei na „cenę” zastosowania struktury laminowanej zamiast monolitycznej. Im bliżej σex do σex-m, tym bardziej skuteczne działanie kompozytowe.

Jeśli σex-f przewyższa f’gd na pewnej długości wokół środka rozpiętości belki, belka może nie przenieść obciążenia. Na całej długości, gdzie σex-f > f’gd, belka jest narażona na pękanie, ale – oprócz niejednorodnego rozkładu defektów – pękanie rozwija się w środku rozpiętości belki.

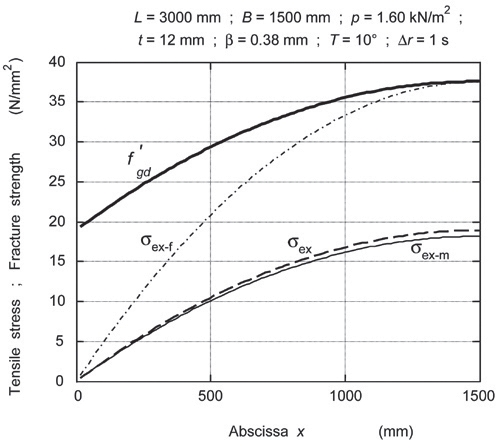
Rys. 9. Równomiernie rozłożone obciążenie wielkości q = 1,50 kN/m działa na płytę LG wykonaną ze szkła o fgd = 19,0 N/mm2 i PVB o GPVB = 0,07 N/mm2. Zastosowane obciążenie jest znacznie niższe niż maksymalnie dopuszczalne.

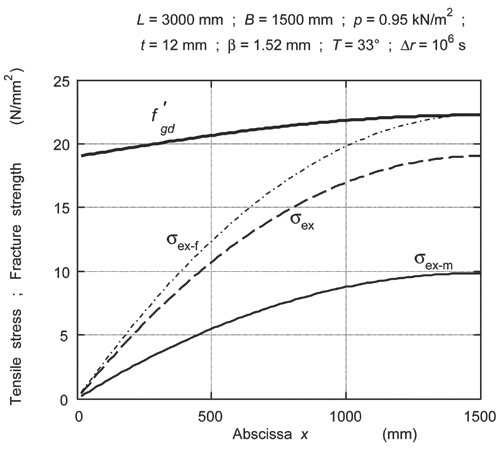
Rys. 10. Równomiernie rozłożone obciążenie wielkości q = 2.40 kN/m działa na płytę LG wykonaną ze szkła o fgd = 19,0 N/mm2 i PVB o GPVB = 105,00 N/mm2. Punkt styku identyfikuje przyłożone obciążenie jako maksymalne

Rys. 11. Równomiernie rozłożone obciążenie wielkości q = 1,425 kN/m działa na płytę LG wykonaną ze szkła o fgd = 19,0 N/mm2 i PVB o GPVB = 0,07 N/mm2. Punkt styczności identyfikuje przyłożone obciążenie jako maksymalne.

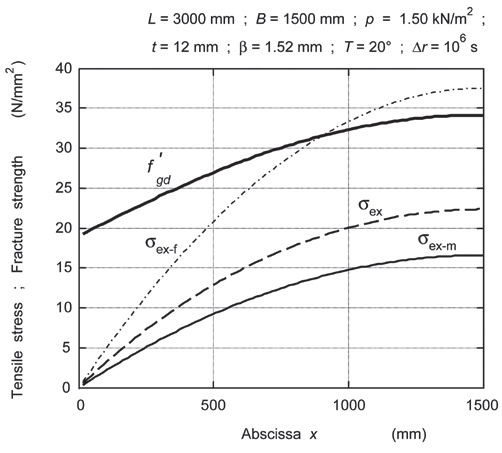
Rys. 12. Równomiernie rozłożone obciążenie wielkości q = 2.40 kN/m działa na płytę LG wykonaną ze szkła o fgd = 19,0 N/mm2 i PVB o GPVB = 0,70 N/mm2. Płyta LG nie przetrwa przyłożonego obciążenia.

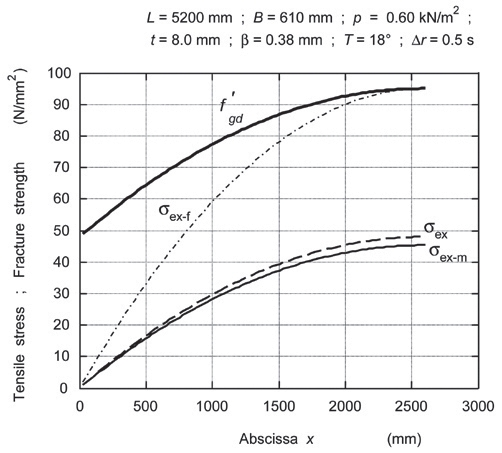
Rys. 13. Równomiernie rozłożone obciążenie wielkości q = 0,37 kN/m działa na płytę LG wykonaną ze szkła o fgd = 48,0 N/mm2 i PVB o GPVB = 12,00 N/mm2. Punkt styczności identyfikuje przyłożone obciążenie jako maksymalne.

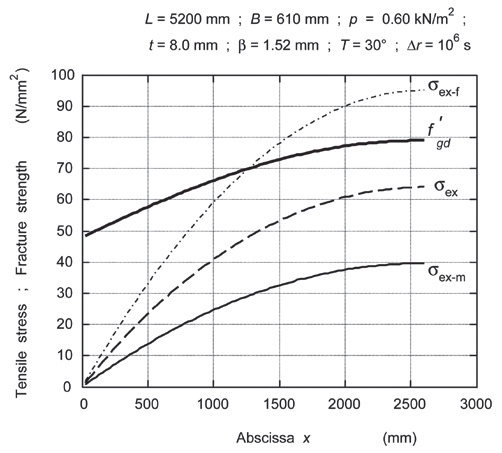
Rys. 14. Równomiernie rozłożone obciążenie wielkości q = 0,37 kN/m działa na płytę LG wykonaną ze szkła o fgd = 48,0 N/mm2 i PVB o GPVB = 0,07 N/mm2. Płyta LG nie przetrwa przyłożonego obciążenia.

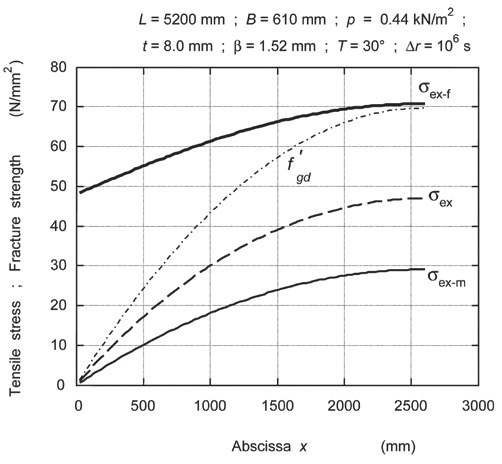
Rys. 15. Równomiernie rozłożone obciążenie wielkości q = 0,27 kN/m działa na płytę LG wykonaną ze szkła o fgd = 48,0 N/mm2 i PVB o GPVB = 0,07 N/mm2. Punkt styczności identyfikuje przyłożone obciążenie jako maksymalne.

Ponieważ f’gd(0)=fgd, jeśli f’gd (0) < σex-f ≤ f’gd (x) dla pewnej długości wokół środka rozpiętości, to taka długość belki nie ulegnie zniszczeniu i belka przeniesie obciążenie tylko ze względu na transfer naprężeń ścinających na granicy szkło- folia PVB.

Jeśli σex > σex-m nawet dla małej długości, to odwrotnie: belka nie przeniesie obciążenia.

Jednym z najważniejszych wyników analizy jest porównanie rzeczywistego obciążenia niszczącego z dwoma granicznymi obciążeniami niszczącymi. W tablicy 1 maksymalne obciążenie belki LG, qud, jest porównywane zarówno do maksymalnych obciążeń uzyskanych odpowiednio z warstwowego modelu analitycznego (założona niska wytrzymałość sklejenia), qf, a monolitycznego modelu analitycznego (założona wysoka wytrzymałość sklejenia), qm. Oczywiście, im bliżej qud do qm (a dalej od qf ), bardziej skuteczne jest działanie przekładek laminujących.

Wnioski
Opisany model różni się od wcześniej pojawiających się w literaturze technicznej zaawansowaniem w obliczaniu wzrostu wytrzymałości w trakcie zginania belki LG, zapewnionego przez zastosowanie folii PVB przekazującej poziome siły ścinania pomiędzy płytami szkła – z możliwością obliczeń analitycznych przy zastosowaniu komputera. Wcześniej znane muszą być tylko parametry PVB dotyczące jej sprężystości.

Prezentacja ma na celu zwrócenie uwagi na względną prostotę różnych algorytmów, zapewniających analityczne relacje między zachowaniem konstrukcji i parametrów projektowych. Takie więc podejście analityczne może służyć również jako narzędzie do projektowania. Ta funkcja jest uznaną za istotną dla szybkiego upowszechniania osiągnięć teoretycznych w praktyce.

Produkty dostępne na rynku szkła architektonicznego były analizowane przez model. Szeroka analiza wykazała niezbicie, jakie czynniki wpływają na zachowania konstrukcji architektonicznej LG, i jak przebiegają ich poszczególne oddziaływania. Jednym z rezultatów badań jest wykazanie nieprawidłowości trzech stwierdzeń, które często pojawiają się w literaturze.

Konstrukcje architektoniczne LG mogą zachowywać się w sposób podobny do szkła monolitycznego o tej samej grubości nominalnej:
- (1) zarówno pod działaniem krótkotrwałego parcia (np. wiatru) na poziomie i poniżej temperatury pokojowej;
- (2) jak też w ramach długotrwałego obciążenia (np. od śniegu) w temperaturze powyżej 0°C;
- (3) w temperaturze ok. 50°C, nawet w przypadku długotrwałego bocznego parcia, zachowanie LG nie może znacząco przypominać charakteru pracy typowego warstwowego produktu.

Paolo Foraboschi
University IUAV of Venice

Całość artykułu w wydaniu drukowanym i elektronicznym 

inne artykuły o podobnej tematyce patrz Serwisy Tematyczne

więcej informacj: Świat Szkła 5/2012

patrz też: 

- Seria norm DIN 18008 do projektowania szklanych elementów konstrukcyjnych , Marcin Kozłowski, Świat Szkła 06/2016

- Szacowanie ugięć wielkoformatowych szklanych ścian osłonowych , Marcin Kozłowski, Świat Szkła 9/2014

- Efekty stosowania nowych norm DIN 18008 w oszkleniach okien i drzwi , Geralt Siebert, Świat Szkła 02/2014

- Naprężenia w uszczelnieniu krawędzi szyb zespolonych , Anneliese Hagl, Świat Szkła 07-08/2013

- Obliczenia szyb zespolonych , Eugen Schuler, Świat Szkła 07-08/2013

- Szkło laminowane kontra materiały wybuchowe, Jens Schneider, John Kuntsche, Świat Szkła 3/2013

- Obciążenia wyjątkowe szkła a bezpieczeństwo , Dobrosława Jaśkowska, Świat Szkła 3/2012

- Dobór szkła na balustrady wg przepisów polskich i niemieckich, Tadeusz Michałowski, Świat Szkła 5/2012

- Szkło laminowane - 10 najważniejszych zalet , Tadeusz Michałowski, Świat Szkła 4/2007