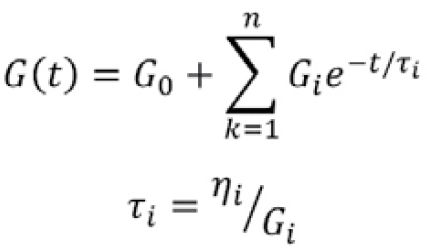Zasada superpozycji1 wpływu czasu i temperatury jest szeroko stosowana do określenia właściwości modułu międzywarstwy (folii laminującej) w postaci krzywych wzorcowych do wykorzystania w projektowaniu szkła.
Proces generowania krzywej wzorcowej można przeprowadzić w jednoznaczny sposób tylko w przypadku materiałów izotropowych.
Generowanie krzywych wzorcowych dla wielowarstwowych folii laminujących (międzywarstw), takich jak trójwarstwowe folie akustyczne o budowie: naskórek-rdzeń-naskórek (skin-core-skin), jest zatem problematyczne.
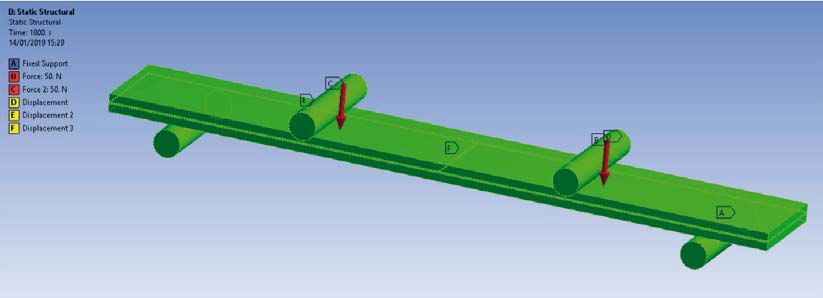
Rys. 1. Konfiguracja próbki do badań dla 4-punktowego zginania
W tym artykule zachowanie laminatu szklanego zawierającego trójwarstwową folię laminującą (międzywarstwę) jest określane przez modelowanie laminatu szklanego w trybie zginania jako układu pięciowarstwowego [szkło – trójwarstwowa folia (naskórek-rdzeń-naskórek) – szkło] z wykorzystaniem właściwości materiału składowego poszczególnych warstw.
Moduł międzywarstwy (folii laminującej), dla którego układ trójwarstwowy (szkło-międzywarstwaszkło) zachowywałby się tak samo jak układ pięciowarstwowy dla danej temperatury i czasu trwania, nazywany jest efektywnym modułem międzywarstwy. Ten efektywny moduł jest określany i może być stosowany w konwencjonalnym oprogramowaniu do analizy
Metodą Elementów Skończonych (MES) lub w ocenie analitycznej do modelowania zachowania się szkła laminowanego, dla scenariusza obciążenia podobnego do warunków, dla których obliczono równoważny moduł. Efektywny moduł uzyskany przez modelowanie w ten sposób powinien być porównywalny z modułem określonym eksperymentalnie na rzeczywistych laminatach szklanych, w poniższym artykule zostaną podane wstępne wyniki analiz.
Wprowadzenie
W ciągu ostatnich 15 lat kilka firm chemicznych opracowało folię laminującą (międzywarstwę) na bazie PVB (Poliwinylobutyral – tworzywo termoplastyczne z grupy acetali poliwinylowych) o ulepszonych właściwościach akustycznych.
W większości przypadków warstwa pośrednia (folia laminująca) składa się z wielowarstwowej struktury ze stosunkowo miękką warstwą rdzenia odpowiadającą za właściwości akustyczne. Obie warstwy naskórka mają raczej standardowe właściwości mechaniczne, przyczyniając się do „wygodnego” transportu i przetwarzania produktu (folii laminującej) oraz wytworzenia odporności na uderzenie (udarności) gotowego laminatu.
Jednak obecność warstwy miękkiego rdzenia ma znaczący wpływ na właściwości mechaniczne laminowanego szkła. Podczas przykładania obciążenia (obciążenie wiatrem lub inne) będą miały silny wpływ, na odkształcenie, właściwości mechaniczne i efektywną grubość warstw składowych.
Metoda, którą należy zastosować do rozważenia wpływu międzywarstwy (folii laminującej) na właściwości mechaniczne, w dużym stopniu zależy od stosowanej normy krajowej [1]. Jednak w większości przypadków preferowany jest bezpośredni pomiar właściwości dynamicznych międzywarstwy.
Najlepiej, gdy ten pomiar uzyskuje się za pomocą dynamicznej mechaniczno-termicznej analizy (dynamic mechanical thermal analysis DMTA2), którą należy przeprowadzić w trybie rozciągania lub ścinania ([2], [3]).
Ogólnie rzecz biorąc, ze względu na lepkosprężyste właściwości warstwy pośredniej (folii laminującej), dane dotyczące modułów są określane jako funkcja temperatury i czasu (lub częstotliwości) i przenoszone na krzywą wzorcową przy użyciu zasady superpozycji wpływu czasu i temperatury (time-temperature superposition TTS).
Ta ostatnia może być stosowana na materiałach reologicznie prostych, nie wykazujących zmian we właściwościach fizycznych lub chemicznych w rozważanym zakresie temperatur. W przypadku międzywarstwy opartej na PVB podejście to ma zastosowanie między temperaturą zeszklenia Tg3, a temperaturą bliską 90°C.
O tej maksymalnej granicznej wielkości temperatury decyduje przede wszystkim obecność grup hydroksylowych w jego składzie chemicznym, które pozwalają na tworzenie wiązań wodorowych i nadają PVB charakter struktury usieciowanej fizycznie.
Ponieważ wiązania wodorowe mają tendencję do rozpadu w podwyższonych temperaturach, założenie o prostym reologicznie materiale można utrzymać tylko do początkowego rozpadu tej fizycznie usieciowanej sieci. Jednak w przypadku wykorzystywania wielowarstwowej folii laminującej pojawia się drugi problem.
Materiał rdzenia, jak i naskórka mają różne właściwości mechaniczne, różne wartości temperatury zeszklenia i różną zależnością właściwości poszczególnych warstw w funkcji czasu/temperatury.
Obecnie nie jest jasne, jak ta warstwowa struktura może wpływać na możliwość zastosowania zasady superpozycji wpływu temperatury i czasu przy wykonywaniu przemiatania (przeczesywania)w różnych częstotliwościach w różnych temperaturach bezpośrednio na strukturze warstwowej.
Ponadto eksperymenty (badania) w zakresie dynamicznej mechaniczno-termicznej analizy DMTA można prowadzić zarówno w trybie rozciągania, jak i ścinania. W przypadku systemów monolitycznych właściwości określone w obu trybach (Moduł Younga E i Moduł Kirchoffa G4) są połączone za pomocą współczynnika Poissona (określa stosunek odkształcenia poprzecznego do odkształcenia podłużnego przy osiowym stanie naprężenia, nie określa sprężystości materiału, a jedynie sposób, w jaki się on odkształca).
W przypadku struktury wielowarstwowej nie można już zastosować prostej zależności. Naprężenia indukowane (powstałe) w międzywarstwie (folii) poddanej niewielkiemu odkształceniu będą zupełnie inne w przypadku odkształcenia struktury wielowarstwowej w trybie ścinania lub rozciągania.
|
1 Zasada superpozycji (w mechanice) – zasada głosząca, że suma przyczyn (np. działających sił) wywołuje skutek (np. przemieszczenie, naprężenie) będący sumą skutków pochodzących od poszczególnych przyczyn;
2 Dynamiczny analizator mechaniczno-termiczny (DMTA) – służy do pomiaru właściwości mechanicznych i lepkosprężystych materiałów - wyznacza amplitudy siły i przemieszczenia oraz przesunięcia fazowe. DMTA to ważne narzędzie stosowane do pomiaru właściwości mechanicznych i lepkosprężystych materiałów, takich jak tworzywa termoplastyczne, tworzywa termoutwardzalne, elastomery, ceramika i metale. W DMTA próbka jest poddawana okresowemu naprężeniu w jednym z kilku różnych trybów odkształcenia (zginanie, rozciąganie, ścinanie i ściskanie). Mierzony jest moduł jako funkcja czasu lub temperatury i dostarcza informacji o przejściach fazowych. Technologia DMTA jest idealnym rozwiązaniem, gdy wymagana jest maksymalna dokładność, a materiał musi być charakteryzowany w szerokim zakresie sztywności i / lub częstotliwości.
3 Temperatura zeszklenia, temperatura witryfikacji (symbol: Tg) – temperatura, w której następuje przejście ze stanu ciekłego lub plastycznego w stan szklisty, czego objawem jest skokowy wzrost lepkości substancji. Jest to jedna z ważniejszych wielkości charakteryzujących właściwości plastyczne szkieł, polimerów (w tym elastomerów) oraz termoplastycznych tworzyw sztucznych.
4 Moduł Younga (E) – inaczej moduł odkształcalności liniowej albo moduł (współczynnik) sprężystości podłużnej – wielkość określająca sprężystość materiału przy rozciąganiu i ściskaniu. Moduł Kirchhoffa (G) (inaczej moduł odkształcalności postaciowej albo moduł sprężystości poprzecznej) – współczynnik uzależniający odkształcenie postaciowe materiału od naprężenia, jakie w nim występuje, jest to wielkość określająca sprężystość materiału. Moduł Kirchhoffa dla materiałów izotropowych bezpośrednio zależy od modułu Younga i liczby Poissona: G=E/2(1+ν) gdzie: ν – współczynnik Poissona.
|
W tym ostatnim przypadku wszystkie warstwy będą wykazywać te same wartości odkształcenia, a na wielkość naprężeń będą silnie wpływać właściwości i grubość warstw naskórkowych (powierzchniowych).
W przypadku odkształcenia wywołanego ścinaniem (naprężeniem stycznym) wywołane odkształcenie nie będzie identyczne w warstwie naskórkowej i rdzeniowej, a dokładne wielkości odkształcenia zostaną określone przez efektywne grubości poszczególnych warstw i odpowiadające im właściwości mechaniczne.
Celem niniejszego artykułu jest zbadanie wyżej wymienionych zagadnień i zweryfikowanie, w jaki sposób pomiary w zakresie dynamicznej mechaniczno- termicznej analizy DMTA właściwości mechanicznych całej międzywarstwy mogą być wykorzystane do przewidywania odkształcenia szkła laminowanego poddanego obciążeniu.
Metoda
Z pierwszych reguł nie jest oczywiste, czy superpozycję wpływu czasu i temperatury (TTS), a tym samym konstruowanie krzywych wzorcowych, można zastosować bezpośrednio przy warstwowej strukturze materiału. Aby to zbadać, wygenerowano krzywe wzorcowe na podstawie eksperymentów dynamicznych, zarówno dla całej folii wielowarstwowej, jak i na poszczególnych warstwach folii.
Ponieważ folie (międzywarstwy) ulegają deformacji w trybie ścinania (tryb II) podczas zginania panelu ze szkła laminowanego, eksperymenty DMTA również przeprowadzono w tym samym trybie. Ma to szczególne znaczenie dla scharakteryzowania całej struktury wielowarstwowej, w której wartości całkowite odkształcenia będą różne w warstwach naskórka (powłoki zewnętrznej) i w rdzeniu.
Dzięki unikalnemu pomiarowi w trybie ścinania zakłada się, że sposób podziału odkształcenia na naskórek i rdzeń będzie identyczny zarówno w trybie testowym (eksperymentalnym), jak i w rzeczywistym zastosowaniu.
Krzywe wzorcowe reologiczne, wyrażone w postaci spektrum (zakresu) relaksacji lub szeregu Prony- ’ego, zastosowano w modelu analizy Metodą Elementów Skończonych MES dla 4-punktowego zginania, aby określić całkowite odkształcenie laminatu w różnych scenariuszach temperatur i obciążeń.
Porównano wyniki odkształcenia, uzyskane dla pojedynczej warstwy lub przy montażu wielu warstw w połączeniu z odpowiednim działaniem materiałów składowych (składników), aby zweryfikować słuszność zasady TTS zastosowanej bezpośrednio do struktury wielowarstwowej. Model analizy MES dla 4-punktowego zginania został również zweryfikowany przy użyciu danych eksperymentalnych.
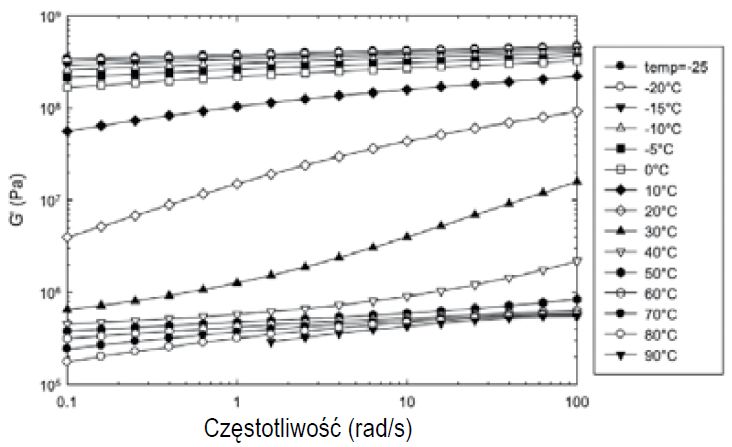
Rys. 2. Wartości modułu G w zależności od częstotliwości dla warstwy naskórka
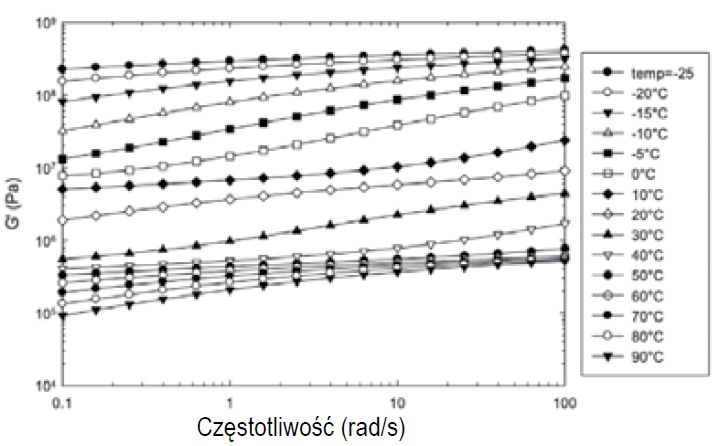
Rys. 3. Wartości modułu G w zależności od częstotliwości dla folii QS41 (krzywe ograniczone do danych dla modułu zachowawczego)
Prace eksperymentalne
Dynamiczne eksperymenty
Eksperymenty dynamiczne przeprowadzono na dwóch foliach (międzywarstwach) Saflex® Acoustic (QS). Dwa typy folii, QS31 i QS41, zostały użyte do zbadania wpływu stosunku grubości warstwy rdzeniowej do grubości warstwy naskórkowej na generowane spektrum relaksacji. Ponadto, funkcje materiału zostały również wygenerowane oddzielnie (indywidualnie) dla warstwy naskórka i warstwy rdzeniowej.
Eksperymentalnie przemiatanie („przeszukiwanie”, przebadanie) częstotliwości przeprowadzono w przedziale częstotliwości od 0,1 rad/s do 100 rad/s. Temperatura w trakcie eksperymentu wzrastała od -30°C do 90°C, zaczynając znacznie poniżej temperatury zeszklenia warstwy rdzeniowej. Próbki miały strukturę złożoną z równoległych płytek o średnicy 8 mm.
Użycie większej średnicy płytki w połączeniu z eksperymentami/badaniami w niskiej temperaturze i z wyższymi częstotliwościami generalnie powoduje przeciążenie konwertera, co nie jest zalecane. Dla każdej temperatury sprawdzono, czy przyłożone odkształcenie utrzymywało się w liniowym obszarze lepkosprężystym.
W przypadku eksperymentów dynamicznych monitorowano kształt mierzonej fali sinusoidalnej, aby upewnić się, że nie wystąpił poślizg na granicy łączenia elementów próbki.
Aby zweryfikować potencjalną zależność spektrum relaksacji od urządzenia pomiarowego, przeprowadzono eksperymenty na dwóch różnych analizatorach, tj. z kontrolowanym odkształceniem (Ares-G2 firmy TA Instruments) i z kontrolowanym naprężeniem (DHR3 firmy TA Instruments). W obu przypadkach zapewniono odpowiednią kontrolę temperatury stosując system ogrzewania konwekcyjnego.
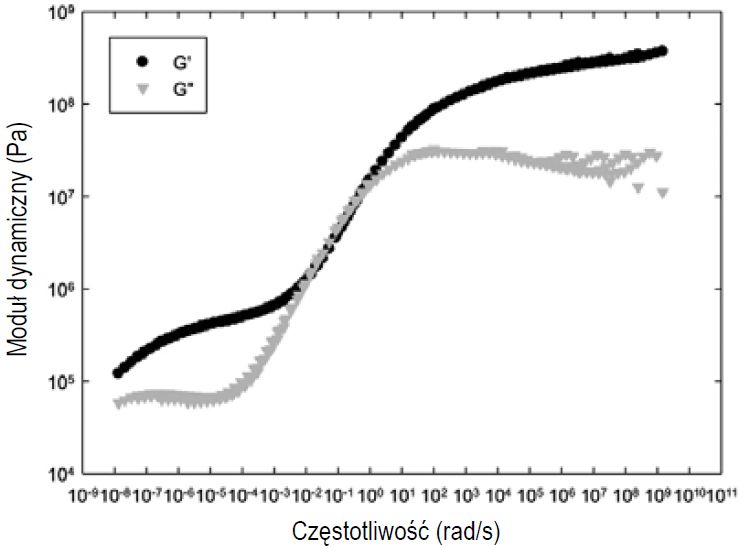
Rys. 4. Krzywa wzorcowa modułów dynamicznych dla warstwy naskórka
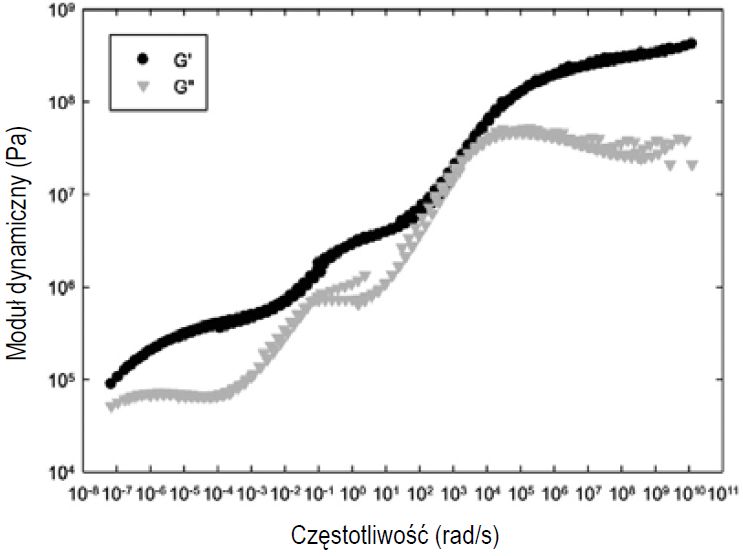
Rys. 5. Krzywa wzorcowa modułów dynamicznych dla systemu wielowarstwowego
(...)
Modelowanie MES
Model MES do eksperymentu z 4-punktowym zginaniem został utworzony w programie Ansys® Mechanical, zgodnie z budową próbki zastosowaną w zestawie doświadczalnym (norma ASTM, C158-2). Rozmiar szklanego panelu dla tego zestawu wynosił 250 mm długości i 38 mm szerokości (rys. 1). Na grubości międzywarstwy i szkła siatka geometryczna składała się z co najmniej 3 elementów.
W przypadkach, w których międzywarstwę (folię PVB) modelowano przy użyciu oddzielnych modeli materiałowych dla rdzenia i naskórka, każda warstwa była modelowana na dokładnej grubości również z co najmniej 3 elementami. W globalnym modelu materiałowym ta konfiguracja i gęstość siatki zostały zachowane, ale każda warstwa miała identyczne właściwości lepkosprężyste, jak opisano w serii Prony, pochodzącej z eksperymentów na globalnym systemie wielowarstwowym.
W tym ostatnim przypadku zweryfikowano wpływ gęstości siatki na ostateczne odkształcenie, aby upewnić się, że wynik jest niezależny od rozmiaru oczka. Należy zwrócić uwagę, że kontakt między powierzchnią szkła, a rolką podpierającą został zdefiniowany jako pozbawiony tarcia, umożliwiający swobodny ruch krawędzi laminatu. Zabrania się przesuwania laminatu wzdłuż osi rolki podpierającej.
We wstępnym eksperymencie obciążenie zwiększano od 0 do 50 N na każdą rolkę dociskającą w przedziale czasowym 1 sekundy i utrzymywano na stałym poziomie przez pozostałe 1800 sekund, zmuszając warstwę pośrednią (polimerową folię laminującą) do pojawienia się zjawiska pełzania w warunkach stałego obciążenia. Przemieszczenie zarówno dociskających rolek, jak i środka laminatu monitorowano jako funkcję czasu i porównano z danymi z modelu symulacyjnego.
W innym modelu symulacyjnym siłę przykładano w szeregu przedziałów czasowych, typowych dla różnych scenariuszy obciążenia, a odkształcenie określano w punkcie, w którym obciążenie osiągnęło maksymalną wartość.
Wyniki
Eksperymenty reologiczne
Rysunki 2 i 3 ilustrują wyniki poszczególnych przemiatań częstotliwości (pomiarów dla różnych częstotliwości) odpowiednio dla pojedynczej warstwy naskórka i próbki wielowarstwowej w zakresie temperatur od -25°C do 90°C. Ze względu na przejrzystość pokazano tylko moduł zachowawczy5 (storage modulus).
Krzywe dla pojedynczej warstwy naskórka można podzielić ogólnie na następujące strefy:
(1) pierwsza strefa odpowiadająca stanowi szklistemu (szklanemu) określanego także jako zeszklenie (glassy state), w którym moduł prawie nie zmienia się wraz z częstotliwością. Temperatura w tym obszarze dla danego polimeru jest zbyt niska, aby zapewnić ruch cząsteczki. Stąd ruch cząsteczek jest zamrożony w tym obszarze. W tym obszarze właściwości mechaniczne są podobne jak dla materiałów krystalicznych (kryształów) – materiały stają się twarde i kruche.
(2) druga strefa w zakresie temperatur od 10°C do 40°C, gdzie moduł silnie zależy zarówno od częstotliwości, jak i temperatury, charakterystyczny dla strefy przejściowej od stanu zeszklenia do elastycznego (glass transition zone) W tym obszarze polimer przechodzi w stan powyżej temperatury zeszklenia.
Powyżej Tg energia cieplna dostarczana przez otoczenie jest wystarczająca, aby odmrozić ruch cząsteczek. Cząsteczki mogą mieć lokalny ruch w tym obszarze, co prowadzi do gwałtownego spadku sztywności w porównaniu z obszarem 1.
(3) Trzecia strefa odpowiadająca obszarowi elastycznemu/ gumowemu (rubbery region) o ogólnie takich samych właściwościach jak pierwsza strefa, ale charakteryzująca się niższą wielkością modułu. Ta strefa nazywana jest też regionem plateau (płaskowyżu) elastycznego (liniowego obszaru lepkosprężystego – linear viscoelastic region).
Wszystkie liniowe modele lepkosprężyste można przedstawić za pomocą równania Volterry łączącego naprężenie i odkształcenie. Liniowa lepkosprężystość ma zwykle zastosowanie tylko do małych odkształceń. Nieliniowa lepkosprężystość występuje, gdy funkcji nie można rozdzielić. Zwykle dzieje się tak, gdy odkształcenia są duże lub gdy materiał zmienia swoje właściwości pod wpływem odkształceń.
(4) Zachowanie w tym obszarze – „płynięcie” jest silnie zależne od czasu. Polimery w tym regionie wymagają zastosowania superpozycji czasu i temperatury, aby uzyskać bardziej szczegółowe informacje i ostrożnie zdecydować, jak wykorzystać materiały. Na przykład, jeśli materiał jest używany w celu radzenia sobie z krótkim czasem interakcji, może prezentować się jako „twardy” materiał. Używając go do celów związanych z długim czasem interakcji, zachowywałby się jak „miękki” materiał.
(5) Lepki polimer łatwo „płynie” w tym obszarze. Kolejny znaczący spadek sztywności. Materiał przechodzi w stan plastyczny/płynny.
Dane dla folii wielowarstwowej (QS41) wykazują podobny trend z tym, że zasięg strefy szklistej jest znacznie mniej wyraźny, a przejście od strefy szklistej do strefy elastycznej (gumowatej) następuje w znacznie szerszym zakresie temperatur od -15°C do 40°C: jest to spowodowane obecnością dwóch przejść ze stanu szklistego (szklanego) dla naskórka i warstwy rdzeniowej. Stosując zasadę superpozycji wpływu czasu i temperatury można rozszerzyć zakres pomiarowy w temperaturze pokojowej na znacznie większą skalę czasu.
Zasada zakłada, że podwyższona temperatura przyspiesza te same ruchy molekularne, które w przeciwnym razie zachodziłyby wolniej w niższej temperaturze.
Ponieważ charakter polimeru zarówno w naskórku, jak i w rdzeniu jest identyczny, można oczekiwać podobnych ruchów molekularnych. Jedynie kinetyka ruchów ma się różnić ze względu na różnicę wolnej objętości między obiema warstwami, na którą wpływa różnica w zawartości plastyfikatora. Krzywe wzorcowe, w temperaturze odniesienia 20°C, uzyskane w wyniku procesu przesunięcia, zarówno dla warstwy naskórka, jak i dla produktu wielowarstwowego przedstawiono na rysunkach 4 i 5.
Można zauważyć wyraźne rozróżnienie w kształcie krzywej. W przypadku warstwy naskórka lub ogólnie pojedynczej warstwy istnieje pojedyncze przejście między stanem szklistym i elastycznym. Z drugiej strony, w przypadku systemu wielowarstwowego występuje pośredni plateau, identyfikujący obecność dwóch głównych mechanizmów relaksacji przesuniętych w czasie lub zakresie częstotliwości.
Mogą być one ponownie związane z obecnością dwóch wyraźnie oddzielonych przejść ze stanu szklistego do elastycznego. Jak widać na rys. 5, generowanie krzywych wzorcowych nie zawsze prowadzi do gładkiej krzywej modułu stratności. Części krzywej, szczególnie przy wyższych częstotliwościach, nie są ze sobą idealnie skorelowane.
Dzieje się tak głównie przy najwyższych częstotliwościach w połączeniu z niższą temperaturą i może być potencjalnie przypisane podatności sprzętu na nieregularne przeszacowanie plastycznej części odkształcenia.
Na szczęście ten brak korelacji nie wpłynie na obliczone odkształcenie laminatu, ponieważ odpowiedź mechaniczna układu będzie całkowicie zdeterminowana wartością modułu zachowawczego (storage modulus), który w tym zakresie częstotliwości silnie przewyższa moduł stratności (loss modulus).
W przypadku danych wielowarstwowych inną słabość w procesie generowania krzywej wzorcowej można zaobserwować w „zniekształceniu” krzywej modułu stratności w pobliżu pośredniego plateau. Wskazuje to, że zasada superpozycji wpływu czasu i temperatury ma swoje ograniczenia w przypadkach, gdy różne warstwy są charakteryzowane jednocześnie.
Ponownie, wpływ tego braku korelacji na generowanie serii Prony będzie znikomy. Wpływ temperatury na kinetykę ruchu cząsteczek ilustruje zależność współczynnika przesunięcia od temperatury. Zarówno dla pojedynczej warstwy (naskórka), jak i dla produktu wielowarstwowego krzywe te przedstawiono na rys. 6.
5 Moduł sprężystości zespolonej definiuje się jako sumę jego części rzeczywistej i urojonej:
G* = G’ + iG’’
gdzie:
– „i” jest jednostką urojoną
– G’ jest modułem zachowawczym, składową sprężystą, będącą w fazie z naprężeniem - bo reprezentuje naprężenia proporcjonalne do odkształcenia, co jest charakterystyczne dla sił sprężystości.
– G” jest modułem stratności, składową lepką przesuniętą w fazie w stosunku do naprężenia - reprezentuje naprężenia proporcjonalne do szybkości ścinania, co jest charakterystyczne dla sił lepkości.
Moduł zachowawczy G’ jest miarą zmagazynowanej energii, natomiast moduł stratności G” jest miarą energii rozproszonej w postaci ciepła, w czasie jednego cyklu odkształcenia. |
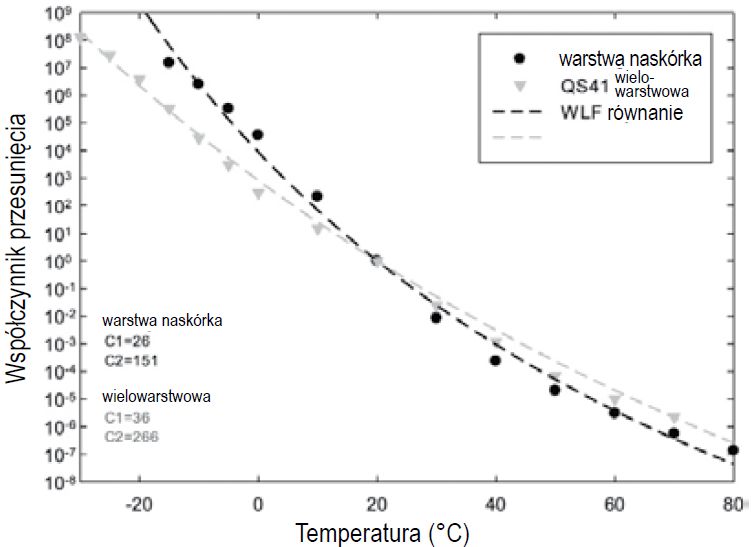
Rys. 6. Zależność współczynnika przesunięcia od temperatury dla międzywarstw jednowarstwowych (naskórek) i wielowarstwowych
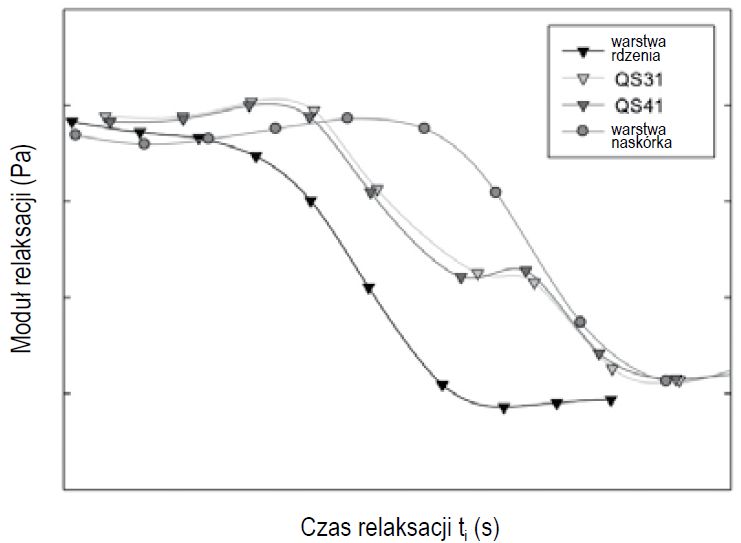
Rys. 7. Spektrum relaksacji dla systemów jedno- i wielowarstwowych (temp. odniesienia = 20°C) model analizy MES
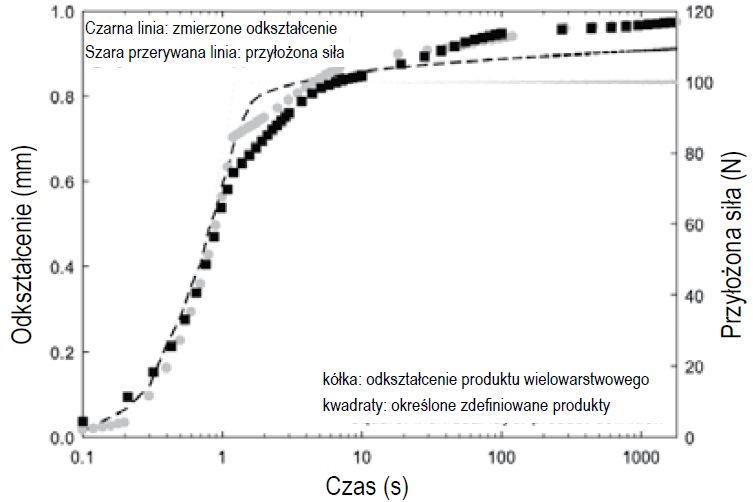
Rys. 8. Zmierzone i obliczone odkształcenie laminatu w badaniach 4- punktowego zginania
Dane eksperymentalne są dopasowane do równania WLF6 określającego wartości dla parametru C1 i C2. W przypadku systemu wielowarstwowego krzywa jest rozciągnięta w większym zakresie częstotliwości, co wyrażają większe wartości C2. Oczekuje się, że rozciąganie stanie się bardziej wyraźne w przypadku wzrostu różnicy wartości Tg (temperatura zeszklenia) dla różnych warstw.
Z krzywej wzorcowej modułów można określić (obliczyć) spektrum relaksacji i / lub szereg Prony’ego. Obie funkcje są matematyczną reprezentacją ruchu cząsteczek zachodzącego w polimerze, który można opisać mechanicznie jako szereg modeli Maxwella [4]:
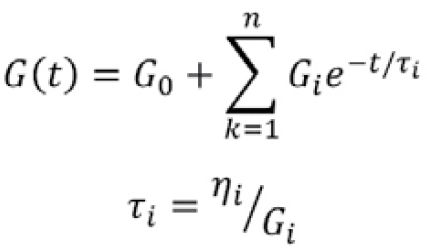
w którym moduł Gi odzwierciedla odnośną wielkość dla każdego procesu, podczas gdy relaksacja wskazuje jego skalę czasową.
Spektrum relaksacji obliczone na podstawie danych eksperymentalnych zilustrowano na rys. 7. Przedstawiono spektrum dla poszczególnych warstw rdzenia i naskórka, a także dla obu systemów wielowarstwowych – folii QS31 i QS41.
Z danych jasno wynika, że zachowania relaksacyjne warstw rdzenia i naskórka występują w zupełnie innych skalach czasowych w tym sensie, że bardziej miękki rdzeń rozluźnia się znacznie szybciej w temperaturze pokojowej. Spektrum relaksacji obu produktów (folii akustycznych) są identyczne i nie mają na nie wpływu różnice odpowiednich grubości poszczególnych warstw, przynajmniej w wąskim zakresie rozważanym w tym artykule.
Spektrum relaksacji dla folii wielowarstwowej znajduje się między spektrum relaksacji dla poszczególnych warstw. Skala czasu dla ruchu molekuł „najwolniejszego” polimeru jest ściśle zgodna z właściwościami warstwy naskórka (zewnętrznej). Jednak relaksacja polimeru warstwy rdzeniowej, mierzona bezpośrednio w folii wielowarstwowej, wydaje się być bardziej ograniczona, co prowadzi do przesunięcia najszybszego przejścia w dłuższych skalach czasowych. w którym moduł Gi odzwierciedla względną wielkość każdego procesu, podczas gdy czas relaksacji τi wskazuje jego skalę czasową.
Spektrum relaksacji obliczone na podstawie danych eksperymentalnych przedstawiono na rys. 7. Wykres przedstawia spektrum dla poszczególnych warstw rdzenia i naskórka, a także dla obu systemów wielowarstwowych QS31 i QS41. Z danych jasno wynika, że zachowanie relaksacyjne warstw rdzenia i naskórka występuje w zupełnie innych skalach czasowych w tym sensie, że bardziej miękka warstwa rdzeniowa „rozluźnia się” znacznie szybciej w temperaturze pokojowej.
Spektrum relaksacji obu folii akustycznych są identyczne i nie ma na nie wpływu różnica odpowiednich grubości poszczególnych warstw, przynajmniej nie w wąskim zakresie rozważanym w tym artykule. Spektrum folii wielowarstwowej znajduje się pomiędzy spektrum poszczególnych warstw.
Skala czasu najwolniejszego ruchu polimeru jest ściśle zgodna z ruchliwością cząsteczek (molekuł) warstwy naskórka. Jednak relaksacja polimeru warstwy rdzeniowej, mierzona bezpośrednio na warstwie wielowarstwowej, wydaje się być bardziej ograniczona, co prowadzi do przesunięcia najszybszego przejścia w dłuższe skale czasowe.
Spektrum relaksacji przedstawione na rys. 7 zostały wykorzystane w modelu MES do przewidywania odkształcenia laminatu w eksperymencie 4 -punktowego zginania. Model został zweryfikowany za pomocą eksperymentalnego testu 4-punktowego zginania, przy użyciu konfiguracji szkła laminowanego 33.2, w temperaturze 27°C.
Rysunek 8 przedstawia porównanie między danymi eksperymentalnymi, a obliczonymi wynikami z modelu MES. Krzywa obciążenia ilustruje wzrost siły działającej na laminat od 0 N do 50 N, wzrastający w skali czasu co 1 s i utrzymywany na stałym poziomie przez pozostałe 1800 sekund.
Dane doświadczalne dotyczące odkształcenia, mierzone w środku laminatu, śledzą wzrost siły, po którym następuje strefa „stałego” pełzania charakteryzującego się odkształceniem rosnącym liniowo w czasie.
Chociaż przewidywane dane z modelu są w ścisłej zgodności z wartościami eksperymentalnymi, obserwuje się pewne niewielkie odchylenia. Model nieco niedostatecznie przewiduje natychmiastowe odkształcenie laminatu i ma tendencję do przewidywania „większego/nadmiernego” pełzania. Ostateczne przewidywane odkształcenie jest prawie o 10% większe niż wartość zmierzona dla tej konfiguracji i warunków eksperymentalnych.
Należy również zauważyć, że prognozy oparte na modelu określonego materiału i modelu wielowarstwowym są dobrze zgodne. Chociaż wartości końcowego odkształcenia są identyczne, występuje niewielka rozbieżność w odpowiedzi sprężystej przy podejściu opartym na poszczególnych warstwach, wykazującym sztywniejsze zachowanie dynamiczne. Te rozbieżności są również pokazane na rys. 9.
Dane przedstawiają obliczone odkształcenie laminatu przy przyłożeniu siły w różnych skalach czasowych albo przy użyciu definicji produktu dla pojedynczej warstwy, albo spektrum relaksacji z doświadczenia wielowarstwowego. W zależności od scenariuszy obciążenia i temperatury można dokonać różnych obserwacji. W wysokich temperaturach lub w dłuższych skalach czasowych oba zestawy danych są dobrze zgodne.
6 Równanie Williams-Landela-Ferry (lub WLF Równanie) to empiryczne równanie związane z superpozycją wpływu czasu i temperatury.
Równanie WLF ma postać:
log (aT) = [-C1(T-Tr)] / [C2 + (T-Tr)]
gdzie log (aT) to logarytm dziesiętny współczynnika przesunięcia WLF [2], T to temperatura, Tr to temperatura odniesienia wybrana do skonstruowania wzorcowej krzywej zgodności, a C1, C2 to stałe empiryczne dostosowane do wartości parametru superpozycji aT.
Równanie WLF jest konsekwencją superpozycji czasu i temperatury (TTS), która matematycznie jest zastosowaniem zasady superpozycji Boltzmanna. To TTS, a nie WLF, umożliwia zestawienie krzywej wzorcowej zgodności, która obejmuje więcej czasu lub częstotliwości, niż pozwala na to czas dostępny na eksperymenty lub zakres częstotliwości oprzyrządowania, takiego jak dynamiczny analizator mechaniczny (DMA).
Równanie można wykorzystać do dopasowania (regresji) dyskretnych wartości współczynnika przesunięcia aT do temperatury. W tym przypadku wartości współczynnika przesunięcia aT są uzyskiwane z logarytmu przesunięcia poziomego (aT) danych podatności pełzania wykreślonych w funkcji czasu lub częstotliwości w podwójnej skali logarytmicznej, tak że zestaw danych uzyskanych doświadczalnie w temperaturze T nakłada się z danymi ustawionymi w temperaturze Tr. Minimum trzy wartościami T są konieczne w celu uzyskania C1, C2, a zazwyczaj więcej niż trzy substancje. |
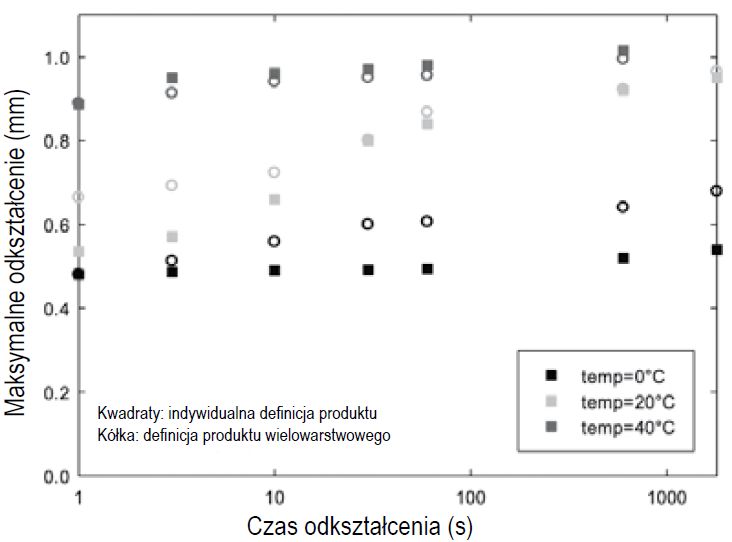
Rys. 9. Obliczone odkształcenie laminatu przy różnych scenariuszach obciążenia i temperatur
Odpowiada to sytuacji, w której oba panele szklane są „odsprzęgnięte” mechanicznie i prawie żadne naprężenia nie są przenoszone na międzywarstwę (folię laminującą). Stąd potencjalne różnice we właściwościach mechanicznych wynikające z różnych podejść nie mają prawie żadnego wpływu na sztywność konstrukcji.
W niższych temperaturach i / lub w krótszych skalach czasowych, podejście z wykorzystaniem pojedynczych warstw przewiduje mniejsze odkształcenie, zgodnie ze sztywniejszym charakterem laminatu. W najgorszym przypadku różnica w przewidywanej sztywności jest bliska 20%. W chwili pisania tego artykułu nie są obecnie dostępne żadne dane doświadczalne dotyczące 4-punktowego zginania w niższej temperaturze, które pozwoliłyby zweryfikować przewidywane dane.
Jednak z krzywej na rys. 8 można wywnioskować, że najwyższa wartość bezpośredniego odkształcenia przed pełzaniem jest najbliżej zgodna z obserwacjami eksperymentalnymi. Oznaczałoby to, że obliczenie widma relaksacji w oparciu o dynamiczną charakterystykę wielowarstwowego materiału w trybie ścinania jest cennym podejściem i ma zastosowanie do obliczeń technicznych wytrzymałości szkła laminowanego.
Wnioski
Obecnie brakuje informacji na temat właściwości mechanicznych międzywarstwy – z folii akustycznej na bazie PVB o strukturze wielowarstwowej. Teoretycznie najdokładniejszym sposobem przewidywania sztywności panelu ze szkła laminowanego jest modelowanie każdej pojedynczej warstwy z osobna i przypisywanie każdej warstwie odpowiedniej funkcji materiału. Jednak takie podejście nie jest wykonalne w przypadku każdego pakietu obliczeniowego MES. Co więcej, nie opublikowano żadnych właściwości mechanicznych izolowanej warstwy rdzeniowej, ponieważ są to informacje poufne.
Zaproponowano tutaj alternatywne podejście, w którym warstwa pośrednia jest scharakteryzowana jako jedna całość w pomiarze DMTA, z wykorzystaniem deformacji trybu II (naprężenia ścinające), i z której pochodzi spektrum/widmo relaksacji dla złożonego produktu. Wykazano, wykorzystując połączenie danych eksperymentalnych i modelowania MES, że podejście to prowadzi do wiarygodnego przewidywania sztywności laminowanego panelu szklanego i że wyniki są zgodne z teoretycznie bardziej rozsądnym podejściem do definicji poszczególnych warstw.
(...)
Pol D’Haene,
Wim M. Stevels
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. Tampere w Finlandii
Bibliografia
[1] Stevels, W.M.: Właściwości modułu folii PVB wg aktualnych norm europejskich (PVB interlayer modulus properties in contemporary European standards). GPD 2019.
[2] ISO 6721-1 Tworzywa sztuczne – Oznaczanie dynamicznych właściwości mechanicznych – Część 1: Zasady ogólne
ISO 6721-2 Tworzywa sztuczne – Oznaczanie dynamicznych właściwości mechanicznych – Część 2: Metoda wahadła skrętnego
ISO 6721-3 Tworzywa sztuczne – Oznaczanie dynamicznych właściwości mechanicznych – Część 3: Drgania zginające – Metoda krzywej rezonansowej
ISO 6721-4 Tworzywa sztuczne – Oznaczanie dynamicznych właściwości mechanicznych – Część 4: Drgania rozciągające – Metoda bezrezonansowa
ISO 6721-5 Tworzywa sztuczne – Oznaczanie dynamicznych właściwości mechanicznych – Część 5: Drgania zginające – Metoda bezrezonansowa
[3] prEN 16613 Szkło w budownictwie – szkło laminowane i bezpieczne szkło laminowane – określenie właściwości mechanicznych międzywarstwy (2013). prEN 16612 Szkło w budownictwie – Wyznaczanie odporności tafli szkła na obciążenia za pomocą obliczeń i testów (2013)
[4] Ferry, J.D.: Właściwości lepkosprężyste polimerów (Viscoelastic properties of polymers). Wiley, New York, 1980.
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 01/2021