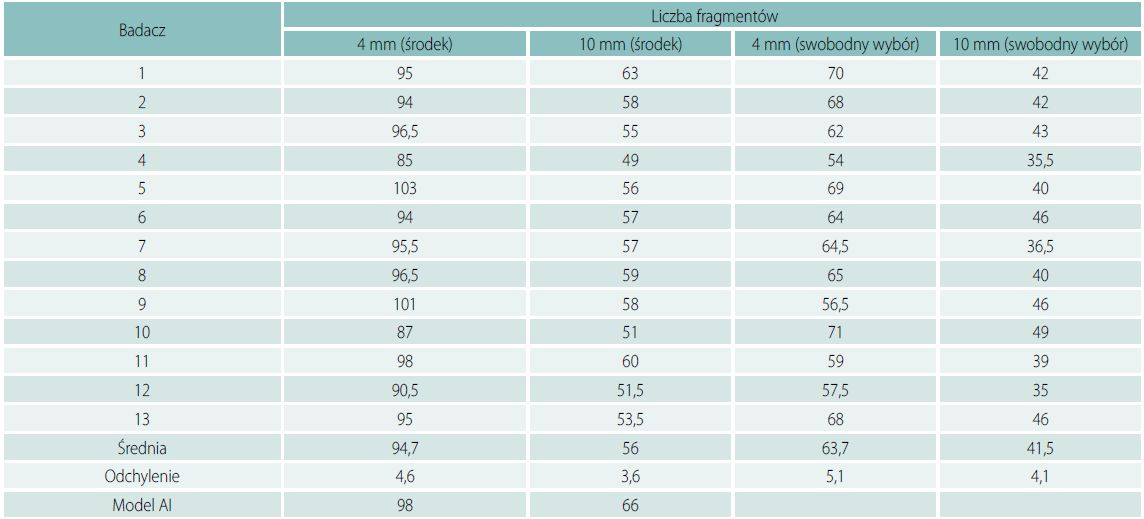
Liczba odłamków w znormalizowanym teście fragmentacji wg normy EN 12150-1 jest sposobem na określenie poziomu bezpieczeństwa szkła hartowanego, a także sposobem na określenie wielkości naprężeń i wytrzymałości szkła hartowanego.
Chociaż sposób obliczania liczby fragmentów jest określony w normie, łącznie z opisem praktycznego przykładu, faktyczny wynik zawsze zależy od badacza. Aby liczenie było spójne we wszystkich badaniach, potrzebny jest automatyczny proces liczenia fragmentów.
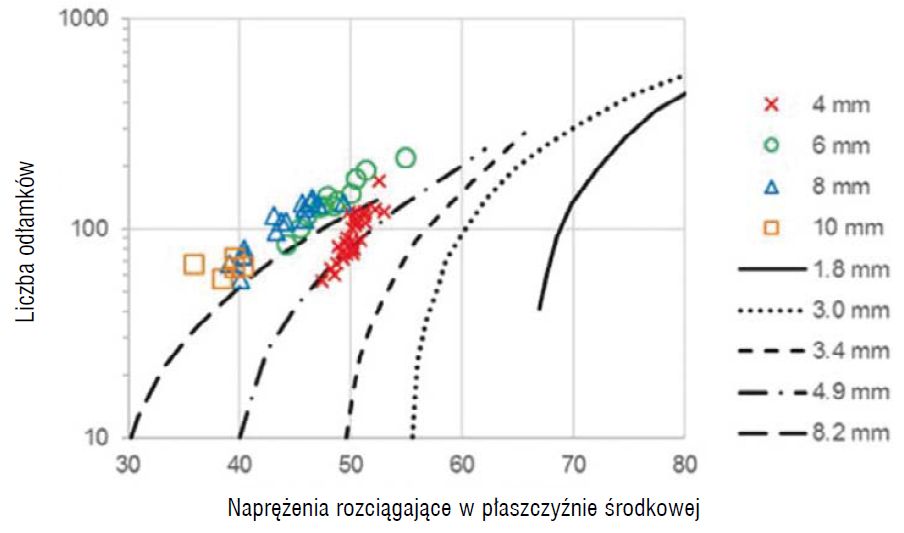
Rys. 1. Zależność między naprężeniem rozciągającym w płaszczyźnie środkowej, a liczbą odłamków na obszarze 50 x 50 mm. Wyniki eksperymentalne dla nominalnych grubości szkła 4 mm, 6 mm, 8 mm i 10 mm oraz dane porównawcze z Akeyoshi i in. [3] dla szkła o grubości 1,8 mm, 3,0 mm, 3,4 mm, 4,9 mm i 8,2 mm
To sprawia, że idealnym rozwiązaniem aplikacja wykorzystująca komputerowy system wizyjny1 (computer vision system), ponieważ komputer nigdy się nie męczy ani nie traci obiektywizmu. Systemy automatycznego liczenia fragmentów już istnieją, ale mają poważne ograniczenia.
Nowoczesne narzędzia i technologie zrewolucjonizowały w ostatnich latach dziedzinę „widzenia” komputerowego (computer vision). Wynika to głównie z postępu w wykorzystywaniu konwolucyjnych sieci neuronowych2, które są szczególnie dostosowane/ wyspecjalizowane do wydobywania wzorców/ zależności i informacji z obrazów/zdjęć.
Aby uczynić systemy liczenia fragmentów bardziej elastycznymi, szybszymi i tańszymi, te ostatnie postępy w dziedzinie komputerowej analizy obrazów umożliwiają wdrożenie automatycznej analizy wizyjnej nawet na smartfonie.
Wprowadzenie
Szkło hartowane jest wytwarzane w procesie obróbki cieplnej, w którym tafla szkła jest najpierw podgrzewana powyżej temperatury przejścia, a następnie szybko schładzana, aby uzyskać odpowiedni gradient temperatury na całej grubości tafli szkła.
Celem jest „zamrożenie” szkła, gdy szkło ma odpowiedni gradient temperatury, a następnie, gdy temperatura się ujednolici, stan wewnętrznych naprężeń wyraża się parabolicznym profilem naprężenia na grubości tafli szkła.
Szkło hartowane ma naprężenia ściskające na powierzchniach zewnętrznych tafli szklanej i naprężenia rozciągające w rdzeniu tafli szklanej. Szkło hartowane ma dwie zalety w porównaniu do odprężonego szkła float. Po pierwsze, wytrzymałość szkła na zginanie i uderzenia wzrasta wraz z wielkością naprężeń ściskających na powierzchni, a po drugie, w przypadku rozbicia – rozpada na małe, nieszkodliwe cząstki z powodu wysokiej indukowanej energii odkształcenia.
Ze względu na te zalety szkło hartowane nazywane jest również szkłem bezpiecznym.
Próba niszcząca - fragmentacja spowodowana pęknięciem szkła to sposób na określenie wielkości naprężeń i poziomu bezpieczeństwa hartowanego szkła. Fragmentacja pokazuje kilka rzeczy wynikających z analizy naprężeń, np. wielkość i równomierność naprężeń. W normie EN 12150-1 [1] zdefiniowano test fragmentacji (rozbicia w wyniku uderzenia), w którym hartowane szkło o wymiarach 1100 x 360 mm2 jest uderzane ostrym narzędziem w środkowym punkcie dłuższej krawędzi.
Na podstawie wzoru spękania, wybiera się obszar, o wielkości 50 x 50 mm, z największymi odłamkami szkła (czyli z minimalną liczbą odłamków) i zlicza te odłamki w tym obszarze. Norma określa minimalną liczbę odłamków, dla różnych grubości szkła, dla uzyskania klasyfikacji bezpiecznego szkła architektonicznego.
Szkło samochodowe ma podobną normę ECE R43 [2] dotyczącą fragmentacji bezpiecznego szkła hartowanego. W porównaniu z normą EN 12150-1, w normie ECE R43 szkło jest uderzane w środkowej części tafli szkła.
Fragmentację szkła i jej związek z wielkością naprężeń badano już w latach 60. XX wieku, czego przykładem są dobrze znane wyniki Akeyoshi i in. [3]. Zdefiniowali zależność między liczbą odłamków, a poziomem naprężenia rozciągającego w rdzeniu (płaszczyźnie środkowej) dla różnych grubości szkła od 1,8 mm do 8,2 mm.
W 1968 roku Barsom [4] opublikował także wyniki dotyczące korelacji naprężenia w rdzeniu (części środkowej) i średniej masy cząstek w rozbitym szkle hartowanym. Ostatnio badania zostały opublikowane przez Pourmoghaddam & Schneider [5] oraz Pourmoghaddam i in. [6], które określają zależność między poziomem naprężenia a fragmentacją, a także przewidują kształt i rozmieszczenie odłamków na podstawie wielkości naprężeń i punktu uderzenia. Liczenie odłamków jest zasadniczo zadaniem wizualnym, w którym człowiek-badacz bardzo efektywnie wykorzystuje swój mózg do oddzielania i policzenia pojedynczych odłamków od potłuczonego szkła.
Dla człowieka zadanie to wydaje się bardzo proste i łatwo jest zapomnieć, że to zadanie wymaga bardzo wyrafinowanych i dobrze rozwiniętych zdolności rozpoznawania „wzorców”, do czego właśnie przeznaczony jest nasz mózg - co osiągnął w rozwoju w czasie ewolucji. Definicja określenia liczby fragmentów jest prosta i przedstawiona na przykładzie opisanym w normie EN 12150-1 [1]. Jednak choć zadanie to może wydawać się łatwe, jest bardzo pracochłonne i czasochłonne.
Proces liczenia jest również bardzo żmudny i podatny na „błędy ludzkie” z powodu braku koncentracji i zmęczenia. W związku z tym możliwe jest, że wyniki liczenia mogą się różnić w zależności od osoby badacza/egzaminatora. Zwłaszcza, gdy liczba odłamków/ fragmentów jest duża, fragmenty mają niewielki rozmiar, a ludzkim okiem może być trudno określić, które z nich są najmniejszymi fragmentami do zliczenia,a także zdefiniowanie, które odłamki znajdują się w obszarze zliczania. W tradycyjnym zautomatyzowanym procesie zliczania - zdjęcie wzoru fragmentacji jest przetwarzane i analizowane za pomocą narzędzi do analizy obrazu [7].
Istnieją urządzenia do automatycznego liczenia fragmentów oparte na analizie obrazu, takie jak skanery odłamków szkła hartowanego: Cullet- Scanner firmy SoftSolution i FROG (Fragment Recognizer On Glass) firmy Deltamax. Niedawno uczenie maszynowe zrewolucjonizowało dziedzinę widzenia komputerowego, ponieważ głębokie sieci neuronowe są w stanie uczyć się bardzo abstrakcyjnych reprezentacji danych bazowych. Daje to nowe narzędzia do analizy wzorców fragmentacji.
|
1 Komputerowy system wizyjny (computer vision system), nazywany również widzeniem komputerowym to układ współpracujących ze sobą elektronicznych urządzeń, którego funkcją jest automatyczna analiza wizyjna otoczenia na podobieństwo zmysłu wzroku u ludzi.
Sieci konwolucyjne poprzez trening są w stanie nauczyć się, jakie cechy szczególne obrazu pomagają w jego klasyfikacji. Ich przewagą nad standardowymi sieciami głębokimi jest większa skuteczność w wykrywaniu zawiłych zależności w obrazach. |
Jednak głębokie sieci neuronowe wymagają dużej ilości danych, dobrze opatrzonych adnotacjami (przykłady skategoryzowanych obrazów z różnych dziedzin). Jest to czasochłonna część tworzenia dobrego modelu do zliczania odłamków/ cząstek szkła.
W tym artykule skupiamy się na przedstawieniu nowatorskiego sposobu liczenia fragmentów szkła hartowanego przy użyciu najnowszych osiągnięć w dziedzinie uczenia maszynowego. Przedstawiono również znaczenie adnotacji danych dla głębokiego uczenia się. Przed rozdziałem o uczeniu maszynowym przedstawiono tło (podstawowe informacje) dotyczące stłuczenia szkła, aby lepiej zrozumieć problemy związane z liczeniem odłamków w szkle hartowanym.
Teoria fragmentacji szkła
Fragmentacja szkła po rozbiciu zależy głównie od naprężeń. W procesie fragmentacji wzrost pęknięć można podzielić na dwie części. Po pierwsze, szkło wymaga wystarczająco wysokiego poziomu naprężeń, aby pęknięcia mogły samoistnie rosnąć. Ten poziom naprężenia jest potrzebny już dla szkła wzmocnionego termicznie, gdy wszystkie pęknięcia powinny dochodzić do krawędzi. Po drugie, dla szkła hartowanego potrzebne jest rozwidlenie pęknięć dla dużej liczby fragmentów. To zjawisko bifurkacji3 wymaga wyższego poziomu indukowanych naprężeń wewnętrznych. [8]
Początkowy punkt pęknięcia i zewnętrzne podparcie lub siła wpływają na fragmentację szkła. Te czynniki mają wpływ na rozkład naprężeń w wierzchołkach pęknięć, przez co zmienia się wzór fragmentacji. [8,9] Z tego powodu początkowy punkt pęknięcia jest określony w normie.
Czas po spękaniu szkła hartowanego, w którym należy policzyć liczbę odłamków, jest ustalony na 3 do 5 minut w normie EN 12150-1 [1]. Jest to również ważne, aby wziąć to pod uwagę, ponieważ po wstępnej propagacji4 pęknięć tworzą się pęknięcia wtórne. Te wtórne pęknięcia są zwykle prostopadłe do początkowych krawędzi pęknięcia, a ich liczba zależy również od początkowego stanu naprężenia.
Zjawisko fragmentacji zachodzi dla cienkich i grubych szkieł. Jednak w przypadku grubszych szkieł krawędzie pęknięć są bardziej szorstkie niż w przypadku cieńszych szkieł. Również w przypadku grubego szkła powierzchnia krawędzi pęknięcia może być pochylona. Typowe pęknięcia szkła o grubości nominalnej 4 mm i 10 mm pokazano jako przykłady, odpowiednio na rys. 9 i 10.
Bardzie chropowata krawędź pęknięcia powoduje szerszą linię pęknięcia, a nachyloną powierzchnię pęknięcia można postrzegać jako biały obszar z powodu silnie rozproszonego odbicia światła od powierzchni pęknięcia. Obie cechy mogą wpływać na wyniki liczenia fragmentów/odłamków szkła. Jednym ze sposobów liczenia odłamków jest zdefiniowanie związku między wielkością naprężeń wewnętrznych w szkle, a liczbą odłamków. Jest to ważne, jeśli sprzęt do optycznego pomiaru naprężeń jest używany do kontroli jakości szkieł hartowanych.
Zależność między naprężeniami rozciągającymi zmierzonymi w płaszczyźnie środkowej za pomocą polaryzatora światła rozproszonego (SCALP-05) [10], a zliczoną liczbą fragmentów/odłamków szkła pokazano na rys. 1.
Badania przeprowadzono na szkle o wymiarach 1100 x 360 mm. Dane z eksperymentu przeprowadzonego przez autorów artykułu porównano z danymi Akeyoshi i in. [3]. Wyniki eksperymentalne autorów podają wyższy poziom fragmentacji szkła w porównaniu z danymi Akeyoshi i in. [3].
Automatyzacja liczenia fragmentów za pomocą „widzenia” maszynowego
Konwolucyjne sieci neuronowe (convolutional neural networks CNN) od dawna dominują w dziedzinie klasyfikacji obrazów i rozpoznawania obiektów. W 2012 r. głęboka konwolucyjna sieć neuronowa (deep convolutional neural network DCNN) po raz pierwszy osiągnęła najlepsze wyniki w konkursie ImageNet Large Scale Visual Recognition Competition (ILSVRC) [11]. Przełomem, który przyniósł DCNN, było to, że nie było już wymagane wyrafinowane/ szczegółowe „ręczne tworzenie” zmiennych do modelu - określenie właściwości obiektu wchodzącego do badań
Przed głębokim uczeniem (deep learning) typowy proces klasyfikacji obrazu wymagałby wyszkolonego klasyfikatora wykonującego „ręcznie” specyfikacje właściwości obiektu („ręcznie” tworzone zmienne).
Stwarza to pewne problemy, ponieważ ludzie niekoniecznie są bardzo skuteczni w definiowaniu cech, które najlepiej różnicują/wyróżniają poszczególne cechy obiektu badanego – „klasyfikację wejściową”.
Zaletą uczenia głębokiego jest to, że specyficzne cechy obiektu potrzebne do wykonania zadania są automatycznie wyodrębniane przez sieć i można ją bezpośrednio trenować/doskonalić od początku do końca, od obrazów wejściowych po klasyfikację wyjściową.
|
3 Bifurkacja [łac. bifurcus ‘widlasty’, ‘rozdwojony’] – zjawisko skokowej zmiany własności modelu matematycznego przy drobnej zmianie jego parametrów (np. warunków początkowych procesu albo warunków brzegowych). Szczególnie często spotykane i istotne jest to pojęcie przy rozwiązywaniu równań różniczkowych oraz badaniu fraktali (i teorii chaosu). Pojęcie bifurkacji zostało wprowadzone przez Henri Poincaré.
|
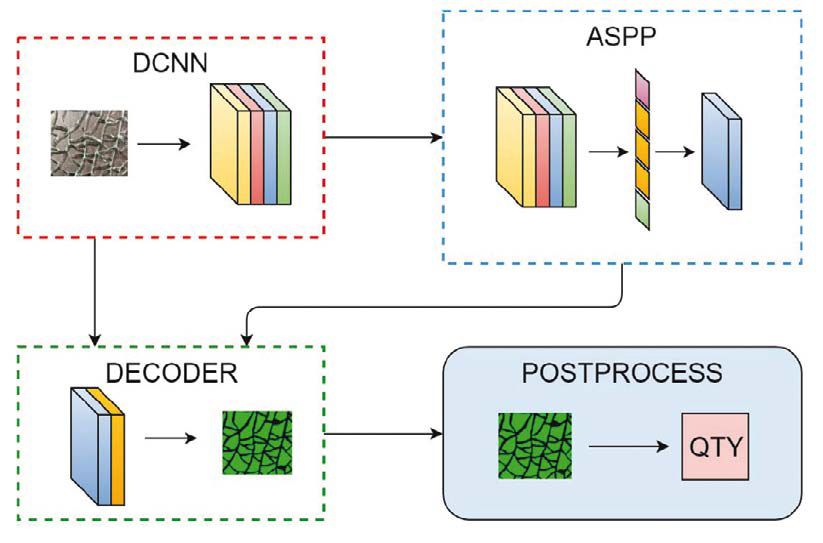
Rys. 2. Proces zliczania fragmentów/odłamków szkła
Jednak segmentacja odłamków szkła to nie tylko problem z klasyfikacją całego obrazu. Jest to raczej problem z klasyfikacją pojedynczych pikseli. Proces, w którym każdy piksel obrazu wejściowego jest klasyfikowany do określonej klasy, nazywany jest segmentacją semantyczną. Po przełomie głębokiego uczenia się nie minęło dużo czasu, zanim nowe technologie mogły zostać przeniesione z klasyfikacji obrazów do segmentacji semantycznej5.
Problem polega na tym, że sieci klasyfikacyjne mają bardzo niską rozdzielczość wyjściową, ponieważ wynik jest definiowany po prostu jako wektor prawdopodobieństw klas (vector of class probabilities).
Jednak w przypadku segmentacji semantycznej rozdzielczość wyjściowa powinna być równa rozdzielczości obrazu wejściowego. Praca Long i in. [12] wykazała, że istniejące sieci klasyfikacyjne można przenieść do sieci segmentacji semantycznej. Dokonano tego poprzez przerzucenie klasyfikacji na w pełni połączone sieci neuronowe6 (fully connected neural networks FCNN) poprzez dodanie interpolacji7 (upsampling) w sieci i zdefiniowanie dopuszczalnych strat na każdy pojedynczy pixel (pixelwise loss). Praca Long i in. była nadal tylko pierwszym krokiem w kierunku skutecznej segmentacji semantycznej.
Od tego czasu coraz bardziej wyrafinowane sieci nieustannie poprawiają coraz bardziej efektywność/ wydajność. W 2018 roku najlepiej działającym modelem do segmentacji semantycznej był DeepLab v3+ firmy Google [13], który również został zaadaptowany w tej pracy do segmentacji fragmentów szkła.
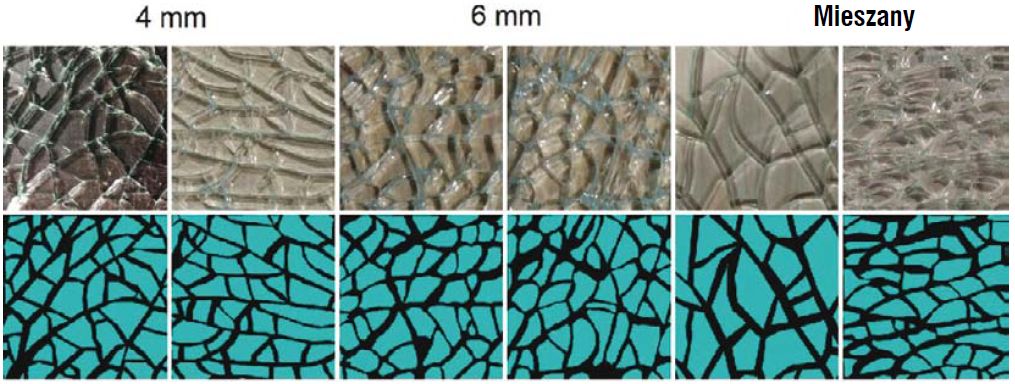
Rys. 3. Próbki surowych/nieprzetworzonych obrazów i odpowiadające im przypisane obszary dla różnych kategorii szkła
Teoria
Teoria stojąca za procesem zliczania fragmentów wykorzystanym w tej pracy jest przedstawiona na rys. 2. Proces składa się z programu/modelu Google DeepLab v3+ do przeprowadzania segmentacji oraz algorytmu przetwarzania końcowego (postprocessing) do faktycznego liczenia.
Bloki DCNN, ASPP i DECODER na rys. 2 są częściami programu DeepLab v3+. Koder jest standardową głęboką konwolucyjną siecią neuronową, która jest używana jako część sieci selekcjonująca wg właściwości (wydzielająca cechy z obrazu wejściowego).
W szczególności w pracy wykorzystano architekturę resztkową sieci (residual network architecture) [14]. Sygnał wyjściowy kodera jest kierowany do modułu rozszerzonej przestrzennej agregacji postrzegania (atrous spatial pyramid pooling ASPP), który próbkuje8 mapę cech z różnymi polami widzenia, aby uchwycić kontekst w wielu skalach (w dużej skali lub małej skali).
Dekoder jest używany do przywracania rozdzielczości przestrzennej do rozdzielczości obrazu wejściowego. Dekoder zasadniczo łączy bogate semantycznie informacje o niskiej rozdzielczości z modułu ASPP z informacjami o wysokiej rozdzielczości przestrzennej z modułu kodera. Rezultatem jest maska segmentacji o wysokiej rozdzielczości – czyli rozdzielczości oryginalnego surowego obrazu wejściowego.
Maska segmentacji podana przez system DeepLab jest dalej przetwarzana końcowo (postprocess) w celu uzyskania liczby fragmentów. Każdy przykładowy fragment szkła jest porównywany z minimalną wartością progową tak, że wszelkie zbyt małe odłamki i puste szczeliny leżące między sąsiednimi fragmentami są pomijane. Następnie liczbę fragmentów można uzyskać w prosty sposób, licząc każdy spójny obszar w binarnej masce segmentacji (binary segmentation mask).
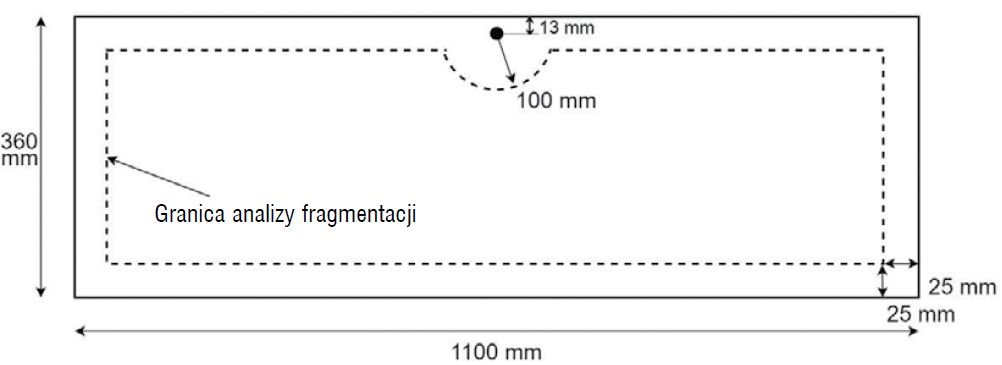
Rys. 4. Obszar „zainteresowania” w analizie fragmentacji wg normy EN 12150-1. Analiza powinna obejmować wszystkie obszary wewnątrz linii przerywanej
Adnotacja/Przypisanie danych
Nowoczesne sieci neuronowe do głębokiego uczenia się w dużym stopniu opierają się na dużej ilości danych, które mogą wykorzystać podczas „treningu modelu”.
Dostosowują swoją wewnętrzną reprezentację zadania, wielokrotnie powtarzając iterację zbioru danych. Przy bardzo „rzadkich” (sparse) danych prowadzi to do prawdopodobnie nadmiernego dopasowania (overfitting) modelu, który nauczył się tylko bardzo określonego zestawu danych. Ten rodzaj modelu zwykle nie jest w stanie uogólnić (wykryć zależności) na całą dziedzinę zadania, co czyni go bezużytecznym w szerszym zakresie zastosowań (taki model, jak „tępy uczeń”, zapamiętał rozwiązania poszczególnych zadań, ale nie znalazł sposobu/zależności do rozwiązywania podobnych/analogicznych zadań).
W przypadku segmentacji odłamków szkła zbiór danych jest dużo prostszy niż np. zróżnicowane obrazy z różnych dziedzin zebrane z internetu. W przypadku segmentacji szkła prezentowana jest tylko jedna klasa obiektów: tylko odłamki szkła. Model sieci neuronowej musi nauczyć się rozróżniać obszary „fragmentowe” (zawierające odłamki odpowiedniej wielkości) i „niefragmentowe” (zawierające odłamki zbyt małej wielkości lub puste przerwy
|
5 Segmentacja obrazu (ang. image segmentation) – proces podziału obrazu na części określane jako obszary (regiony), które są jednorodne (homogeniczne) pod względem pewnych wybranych własności. Obszarami są zbiory pikseli (punktów). Własnościami, które są często wybierane jako kryteria jednorodności obszarów są: poziom szarości, barwa, tekstura. Segmentacja semantyczna jest klasycznym zadaniem widzenia komputerowego, który polega na przyjęciu pewnych danych (np. obrazów 2D) jako danych wejściowych i przekształceniu ich w maskę z wyróżnionymi obszarami zainteresowania. Wcześniejsze zadania związane z widzeniem komputerowym dotyczyły tylko takich elementów, jak krawędzie (linie i krzywe) lub gradienty, ale nigdy nie pozwalały na zrozumienie obrazów na poziomie pikseli, tak jak postrzega je człowiek. Segmentacja semantyczna, która skupia razem części obrazów należące do tego samego obiektu według określonego zainteresowania/zapytania, rozwiązuje te zadania, a tym samym znajduje zastosowanie w niezliczonych dziedzinach.
|

Rys. 5. Wzór fragmentacji w próbce testowej dla szkła o grubości 4 mm

Rys. 6. Wzór fragmentacji w próbce testowej dla szkła o grubości 10 mm

Rys. 7. Mapa termiczna/cieplna pokazująca rozkład fragmentów/ odłamków szkła dla próbki grubości 4 mm i czerwone prostokąty przedstawiające swobodnie wybrane regiony w eksperymencie

Rys. 8. Mapa termiczna/cieplna pokazująca rozkład fragmentów/ odłamków szkła dla próbki grubości 10 mm i czerwone prostokąty przedstawiające swobodnie wybrane regiony w eksperymencie
Przykładem szeroko stosowanego, bardziej złożonego zbioru danych jest ImageNet, który zawiera ponad 15 milionów obrazów należących do około 22 000 różnych kategorii [15]. Obrazy są zbierane z internetu i przypisywane/kategoryzowane przez ludzi. Nowoczesne sieci neuronowe wykazały skuteczność/ wydajność „na poziomie ludzkim” nawet w przypadku bardzo wymagających zestawów danych, takich jak ImageNet [16].
Dodawanie adnotacji do danych jest bardzo czasochłonne i kosztowne ze względu na potrzebę żmudnej i precyzyjnej pracy ludzkiej. Ilość danych jest zwykle „wąskim gardłem” w opracowaniu modelu dobrej jakości/skuteczności, szczególnie gdy mowa jest o wyspecjalizowanych zadaniach i nie ma jeszcze dostępnych adnotacji/kategoryzacji, czyli nie można wykorzystać żadnych swobodnie dostępnych zestawów danych (które ktoś uprzednio wykonał).
Przykładem takiego zadania jest fragmentacja szkła. Aby model nauczył się segmentować fragmenty, trzeba mu pokazać liczne przykłady prawidłowych, bazowych (ground truth) segmentacji.

Rys. 9. Środkowy obszar 50 x 50 mm próbki szkła grubości 4 mm. W segmentacji fragmenty/odłamki graniczne (leżące na granicy obszaru próbki) są niebieskie, a środkowe - żółte. Fragmenty brzegowe liczy się jako „połówki” zgodnie z normą EN 12150-1 [1]

Rys. 10. Środkowy obszar 50 x 50 mm próbki szkła grubości 10 mm. W segmentacji fragmenty/odłamki graniczne (leżące na granicy obszaru próbki) są niebieskie, a środkowe - żółte. Fragmenty brzegowe liczy się jako połówki zgodnie z normą EN 12150-1 [1]
(...)
Juho Ruusunen, Antti Aronen
Glaston Finland Oy
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. Tampere w Finlandii
Bibliografia
[1] EN 12150-1: 2015 Szkło w budownictwie - Hartowane termicznie bezpieczne szkło sodowo-wapniowo- krzemianowe - Część 1: Definicja i opis
[2] E/ECE, 2017, Umowa w sprawie przyjęcia jednolitych warunków homologacji i wzajemnego uznawania homologacji wyposażenia i części pojazdów silnikowych. Uzupełnienie 42, regulamin nr 43, poprawka 4: Jednolite przepisy dotyczące homologacji materiałów oszklenia bezpiecznego i ich instalacji w pojazdach, załącznik 5, kwiecień 2017
[3] Akeyoshi, K., Kanai, E., Yamamoto, K., Shima, S., 1967, Rep. Res. Lab., Asahi Glass., 17, s. 23.
[4] Barsom, J.M., 1968, Spękanie (fragmentaryzacja) szkła hartowanego (Fracture of Tempered Glass), J. Am. Ceram. Soc. vol. 51, s. 75–78. https://doi.org/10.1111/j.1151-2916.1968.tb11840.x
[5] Pourmoghaddam, N. & Schneider, J., 2018, Eksperymentalne badanie wielkości fragmentu szkła hartowanego (Experimental investigation into the fragment size of tempered glass), Glass Struct Eng, tom 3, strony 167-181. https://doi.org/10.1007/s40940-018-0062-0
[6] Pourmoghaddam, N., Kraus, MA, Schneider, J., Siebert, G., 2018, Związek między energią odkształcenia a morfologią wzoru pęknięcia szkła hartowanego termicznie do przewidywania fragmentacji szkła w makroskali 2D (Relationship between strain energy and fracture pattern morphology of thermally tempered glass for the prediction of the 2D macroscale fragmentation of glass), Glass Struct Eng . https://doi.org/10.1007/s40940-018-00091-1
[7] Gordon, G.G., 1996, Zautomatyzowana analiza fragmentacji szkła (Automated glassfragmentation analysis), Proc. Natl. SPIE 2665, Machine Vision Applications in Industrial Inspection IV. https://doi.org/10.1117/12.232245
[8] Gardon, R., 1980, Hartowanie termiczne szkła (Thermal Tempering of Glass), w Glass Science and Technology vol. 5 Elasticity and Strength in Glasses, D.R. Uhlmann i N.J. Kreidl (red.), Academic Press, Nowy Jork, str. 145–216.
[9] Aronen, A., Kocer., C., 2015, Mechaniczna uszkodzenie/ pęknięcie szkła hartowanego; Porównanie norm dotyczących badań i katastrofalnej awarii podczas eksploatacji (The Mechanical Failure of Tempered Glass; a Comparison of Testing Standards and In-Service Catastrophic Failure), GPD 2015, s. 388-391.
[10] Anton, J., Aben, H., 2003, Kompaktowy polaryzator światła rozproszonego do pomiaru naprężeń szczątkowych w płytach szklanych (A Compact Scattered Light Polariscope for Residual Stress Measurement in Glass Plates), GPD 2003, str. 86-88.
[11] Krizhevsky, A., Sutskever, I., Hinton, G.E., 2012, Klasyfikacja ImageNet z głębokimi konwolucyjnymi sieciami neuronowymi, postęp w neuronowych systemach przetwarzania informacji (Imagenet Classification with Deep Convolutional Neural Networks, Advances in Neural Information Processing Systems), Curran Associates, Inc., str. 1097–1105.
[12] Long, J., Shelhamer, E., Darrell, T., 2015, W pełni konwolucyjne sieci do segmentacji semantycznej (Fully convolutional networks for semantic segmentation), 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, s. 3431–3440.
[13] Chen, L., Zhu, Y., Papandreou, G., Schroff, F., Adam, H., 2018, Koder-dekoder z separowalną konwolucyjną siecią do semantycznej segmentacji obrazu (Encoder- Secoder with Atrous Separable Convolution for Semantic Image Segmentation), CoRR, 2018, http:// arxiv.org/abs/1802.02611.
[14] He, K., Zhang, X., Ren, S., Sun, J., 2016, Głębokie uczenie do rozpoznawania obrazu (Deep Residual Learning for Image Recognition), 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, s. 770 -778.
[15] Russakovsky, 0., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., 2015, Wyzwanie związane z rozpoznawaniem wizualnym na dużą skalę (Imagenet Large Scale Visual Recognition Challenge), International Journal of Computer Vision, Vol. 115, str. 211-252.
[16] Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bernstein, M., ILSVRC 2017. http://image-net.org/challenges/LSVRC/2017/results.
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 01/2021