W czasach, gdy komputerowe wspomaganie projektowania jest bardzo powszechne, często spotyka się, że przeprowadzone badania doświadczalne wspomagane są analizami numerycznymi.
Opisane w numerze 3/2009 „Świata Szkła” badania doświadczalne stanowią część przeprowadzonej analizy zachowań szkła mocowanego punktowo.
Przeprowadzony w laboratorium Instytutu Konstrukcji Budowlanych Politechniki Poznańskiej eksperyment wzbogacony został o analizę numeryczną, która została wykonana w środowisku programu ABAQUS/CAE.
Model numeryczny
Działanie programu ABAQUS/CAE oparte jest na Metodzie Elementów Skończonych (MES, ang. FEM, finite element method). Jest to metoda obliczeń fizycznych, opierająca się na dyskretyzacji obszaru na skończone elementy uśredniające stan fizyczny ciała i przeprowadzaniu obliczeń tylko dla węzłów tego podziału. Poza węzłami wyznaczana właściwość jest przybliżana na podstawie wartości w najbliższych węzłach.
Tworząc model numeryczny dąży się do tego, aby w sposób jak najbardziej dokładny odzwierciedlić rzeczywistość i rozpatrywane zagadnienie. Bardzo ciekawym tematem okazała się analiza połączenia mocowania punktowego z taflą szklaną. Analiza ta miała na celu poznanie wartości naprężeń w poszczególnych elementach modelu, a także określenie wartości ugięcia tafli szklanej w zależności od wielkości i powierzchni oddziaływania obciążenia.
Zastanawiano się również, czy i w jakim stopniu założone warunki brzegowe – czyli sposób zamocowania łącznika punktowego oraz rodzaj materiału, z którego wykonana jest podkładka umieszczona między łącznikiem a szkłem – mają wpływ na wielkość obliczanych wartości.
Model numeryczny przygotowany w programie ABAQUS składał się z trzech elementów: szklanej tafli, stalowego łącznika oraz przekładek z tworzywa. Wszystkie elementy modelu zostały zdefiniowane w programie ABAQUS jako 3D (modeling space), DEFORMABLE (type), SOLID (shape). W płycie szklanej modelowano dwa przypadki otworów, o średnicy 20 mm oraz 14 mm, znajdujące się w odległości 50 mm (od osi otworu) do krawędzi tafli.
Przyjęto grubość płyty 8 mm. W doświadczeniu laboratoryjnym tafla szklana mocowana była na 4 łącznikach. Z uwagi na symetrię modelu numerycznego analizowano tylko ¼ płyty. Takie uproszczenia można stosować w obliczeniowych programach numerycznych, co nie wpływa na dokładność wyników, a powoduje znaczne skrócenie obliczeń.
Stalowy łącznik został wymodelowany bez podziału na talerz zewnętrzny, wewnętrzny, śrubę i tuleję. Talerze mocowania i tuleja, które stanowią w rzeczywistości odrębne elementy, w modelu numerycznym stanowiły całość. Odległość w świetle między talerzami została tak przyjęta, aby możliwe było umieszczenie między nimi tafli szklanej (grubość 8 mm) osłoniętej z obu stron przekładkami (każda grubości 3 mm). Przekładki miały średnicę 50 mm. Zewnętrzna średnica kołnierza przekładki wynosiła 14 mm, a wewnętrzna 8 mm.
Poszczególne elementy modelu złożono tak, że płyta szklana osłonięta była z obu stron przekładkami w taki sposób, że kołnierz przekładki chronił wnętrze otworu w szkle przed bezpośrednim kontaktem ze stalową śrubą. Założono w początkowej fazie centryczne ułożenie przekładek względem stalowej części mocowania, jak również centryczne ułożenie zestawu: mocowanie-przekładki w stosunku do otworu w płycie szklanej.
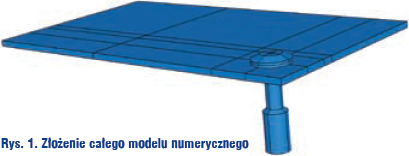
W rzeczywistości jest tak, że współśrodkowe ułożenie zachowuje układ mocowanie-przekładki, gdyż są one w stosunku do trzpienia mocowania wykonane bez luzu. Ułożenie z kolei szyby na czterech mocowaniach tak, aby każde mocowanie było centryczne względem otworu jest już w praktyce przypadkowe. Cały model przedstawia rys. 1.
Materiał
Do każdego z elementów modelu został przypisany materiał liniowo sprężysty, który każdorazowo był scharakteryzowany gęstością, modułem Younga i współczynnikiem Poissona. Szkło, z którego wymodelowana została płyta, zdefiniowano w programie ABAQUS jako materiał liniowy, sprężysty, izotropowy. Do zdefiniowania takiego materiału przyjęto moduł Younga 70 GPa, współczynnik Poissona ν=0,23.
Stal, z której wykonane są łączniki to stal 1.4301, traktowana również jako materiał liniowy, sprężysty i izotropowy (pominięto pracę w zakresie plastycznym i rozpatrywano tylko zakres sprężysty). Przekładki, które zabezpieczają szkło przed kontaktem ze stalą mogą być wykonane z EPDM, poliamidów bądź aluminium lub nylonu. Rodzaj tworzywa, z którego wykonane są podkładki zależy od producenta mocowań, w analizie numerycznej przyjęto do ostatecznej analizy podkładki wykonane z nylonu.
Warunki brzegowe
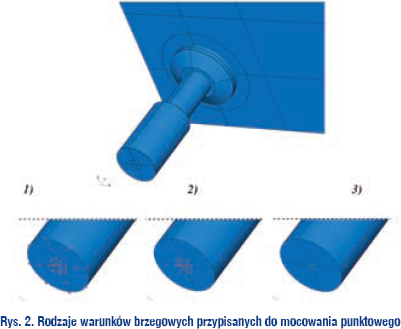
Z uwagi na to, że trudno było dokładnie określić warunki brzegowe występujące w doświadczeniu (jak choćby ustalenie podatności połączenia śrubowego: tuleja-blacha stalowa), w programie ABAQUS/CAE zdefiniowano trzy rodzaje schematów podparcia, co pozwoliło ocenić, jak duży wpływ na wyniki ma odpowiednie przyjęcie sposobu zamocowania.
Założono następujące warunki brzegowe:
- utwierdzenie całej dolnej części łącznika (na całej powierzchni tulejki mocowanej do podkonstrukcji), odebrano wszystkie 6 stopni swobody,
- utwierdzenie na środkowej części dolnej tulejki, również odebrano 6 stopni swobody,
- przegub przyłożony do punktu referencyjnego (TOOLS→REFERENCE POINT) w środku dolnej powierzchni tulejki, do którego przyłączone ( „zszyte” ) zostały pozostałe węzły tej powierzchni, w punkcie RP–1 odebrano 3 translacyjne stopnie swobody (przemieszczenia U1 = U2 = U3 = 0).
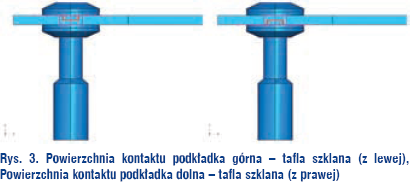
Rozpatrywany model składa się z kilku części, dlatego należy pomiędzy nimi wprowadzić odpowiednie płaszczyzny i warunki kontaktu. Wprowadzono kontakt między szklaną taflą a podkładkami oraz podkładkami a stalowym łącznikiem, polegający na zdefiniowaniu tarcia między poszczególnymi powierzchniami. Algorytm obliczania kontaktu pomiędzy poszczególnymi powierzchniami w programie ABAQUS/CAE bazuje na metodzie iteracyjnej Newtona-Raphsona. Polega ona na tym, że w każdym cyklu iteracyjnym operujemy pełnym obciążeniem P.
W poszczególnych cyklach przyjmujemy stałe, przybliżone macierze sztywności, co powoduje niespełnienie warunków równowagi. Po każdym cyklu obciążenia oblicza się obciążenie niezrównoważone. To obciążenie służy do wyznaczania dodatkowych przemieszczeń, czyli zmian konfiguracji odpowiadającej równowadze. Proces obliczeniowy kończy się w momencie osiągnięcia równowagi. Statyczna równowaga jest wtedy, kiedy działające siły zewnętrzne równoważą się z wewnętrznymi siłami węzłowymi.
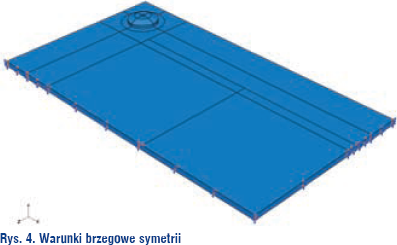
W analizie numerycznej rozpatrywano tylko ¼ całego zadania i z uwagi na to zdefiniowano również warunki symetrii. Symetria po kierunku X blokuje przemieszczenie po kierunku 1 (U1 = 0) oraz obroty po kierunku 2 i 3 (UR2 = UR3 = 0). Natomiast warunek symetrii po kierunku Z uniemożliwia przemieszczenie po kierunku 3 (U3 = 0), a także obroty po kierunku 1 i 2 (UR1 = UR2 = 0). Omówione warunki symetrii przedstawione są na rys. 4.
Obciążenie
W badaniach doświadczalnych obciążenie przykładane było na powierzchnię tafli szklanej za pomocą tłoka prasy. Obciążenie nie było jednak przykładane bezpośrednio do tafli szklanej, ponieważ kontakt stalowego tłoka ze szkłem powodowałby zniszczenie szklanej próbki. Obciążenie przykładane było za pomocą elastomerowych przekładek. W analizie numerycznej zastosowano pewne uproszczenie polegające na obciążeniu siłą 1500 N rozłożoną równomiernie na powierzchni okręgu, odpowiadającej powierzchni elastomerów rozkładających obciążenie od tłoka maszyny wytrzymałościowej.



Siatka elementów skończonych
Wszystkie części modelu zostały podzielone na trójwymiarowe elementy C3D8R (8–node linear brick, reduced integration with hourglass control). Są to elementy, które posiadają trzy stopnie swobody (3 przemieszczenia). Taki rodzaj elementów skończonych ma kształt prostopadłościanu z ośmioma węzłami (w każdym narożu jeden) oraz z 1 punktem całkowania. Siatka elementów skończonych na każdym elemencie modelu definiowana była indywidualnie, tak aby wyeliminować zaburzenia, które mogłyby powodować powstanie koncentracji naprężeń w miejscach, w których takie zaburzenia nie powinny się pojawić.
Bardzo istotnym miejscem w obliczeniach był otwór w szkle na mocowanie punktowe. Dlatego w tym miejscu siatka elementów została zagęszczona, natomiast pozostałą część płyty podzielono ma większe elementy. Podczas analizy zwiększano również liczbę elementów na grubości płyty szklanej. Analizę przeprowadzano dla 4, 6 i 8 elementów na grubości szklanej tafli, aby uzyskać właściwy dla płyty rozkład naprężeń. Zmniejszenie wielkości elementów siatki wykonane zostało także na podkładkach.
Analiza przyjętych warunków brzegowych
Bardzo istotny wpływ na zachowanie się modelu i sztywność całego połączenia ma przyjęcie warunków brzegowych. W rozpatrywanym modelu dotyczy to przyjęcia schematu zamocowania łącznika punktowego do podkonstrukcji. Zgodnie z wcześniejszym opisem i rys.2. rozpatrywano trzy przypadki zamocowania (od utwierdzenia całej powierzchni przylegania tulei do blachy stalowej aż do idealnego przegubu).
Na mapach ugięcia (przykładowo zamieszczono U1 – po kierunku x) z programu ABAQUS widać wyraźne różnice w zachowaniu się mocowania punktowego w zależności od schematu zamocowania rotuli, co ma wpływ na sztywność całego połączenia szkło-łącznik, a tym samym na wartość ugięcia tafli szklanej.
Z map ugięcia stalowego łącznika wynika, jak należało się spodziewać, że największą sztywność ma łącznik całkowicie utwierdzony, ponieważ tuleja mocowania przemieszcza się najmniej ze wszystkich rozwiązań. Przy częściowym utwierdzeniu widoczne jest, że górna część tulei systemowej zaczyna się przemieszczać, co świadczy o mniejszej sztywności całego połączenia. Zdefiniowany w trzecim przypadku przegub pozwala na obrót tulei mocowania. Porównując wymienione rozwiązania z zamocowaniem łącznika sztywnego w badaniu przyjąć należy, że rzeczywistemu modelowi najbliższy będzie przypadek 2.
W eksperymencie łącznik przykręcony jest do blachy za pomocą śruby w taki sposób, że połączenie umożliwiało pewne przemieszczenia łącznika oraz nieznaczne przemieszczenia śruby względem blachy na skutek działania obciążenia na próbkę. Z uwagi na to trudno mówić o całkowitym i sztywnym zamocowaniu badanego laboratoryjnie modelu. Do ostatecznej analizy numerycznej przyjęto rozwiązanie pośrednie (utwierdzenie części powierzchni dolnej mocowania). Analiza pełnego utwierdzenia i przegubu pokazuje, że schemat statyczny modelu i przyjęte warunki brzegowe znacznie rzutują na wyniki analizy. Należy mieć na uwadze, że wprowadzone uproszczenia mogą mieć wpływ na rozbieżność wyników pomiędzy analizą numeryczną a wynikami uzyskanymi z badań laboratoryjnych.
mgr inż. Dariusz Włochal
dr hab. inż. Adam Glema
prof. Tomasz Łodygowski
Politechnika Poznańska
Instytut Konstrukcji Budowlanych
wszytkie artykuły cyklu:
- Łączniki punktowe w szklanych konstrukcjach , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 1/2009
- Projektowanie szklanych konstrukcji mocowanych punktowo , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 2/2009
- Badanie doświadczalne konstrukcji szklanych mocowanych punktowo , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 3/2009
- Analiza numeryczna konstrukcji szklanych mocowanych punktowo cz. 1 , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 4/2009
- Analiza numeryczna konstrukcji szklanych mocowanych punktowo cz. 2 , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 6/2009
patrz też:
więcej informacji : Świat Szkła 4/2009
inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
































