Szyby lite i zespolone montowane w ścianach osłonowych, w większości podpierane są na obwodzie. W ścianie słupowo-ryglowej szyba osadzana jest w aluminiowych profilach słupów i rygli za pośrednictwem listew dociskowych i uszczelek EPDM. Typowy sposób osadzania szyby zespolonej w ścianie słupowo-ryglowej przedstawia rys. 1.
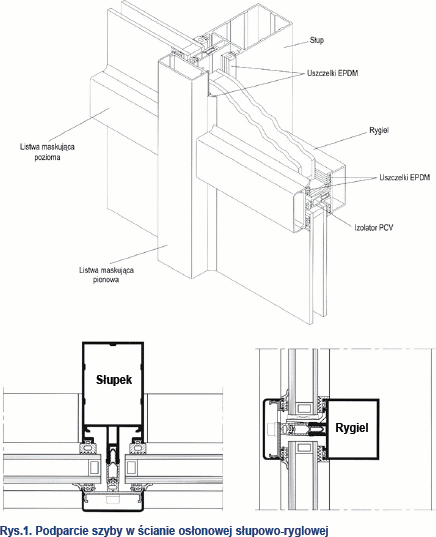
Stabilność szyby zapewniana jest przez jej ustawienie na podkładkach podpierających oraz przez obwodowy docisk listew wraz z uszczelkami. Dwie podkładki podpierające ustawione są pod dolną krawędzią szyby, w odległości do 150 mm od naroży. Zadaniem tych podkładek jest przeniesienie ciężaru własnego szyby na konstrukcję nośną (rygiel) ściany osłonowej.
Docisk obwodowy stabilizuje szybę i zapobiega jej wypadnięciu przy obciążeniu prostopadłym do ściany (np. wiatr), ale pozwala na przesuw w płaszczyźnie szyby, co umożliwia kompensację przemieszczeń spowodowanych rozszerzalnością liniową szkła przy obciążeniach termicznych.
Uproszczonym odwzorowaniem opisanego wyżej sposobu podparcia są podpory przegubowo-przesuwne, z czego podkładki podporowe podpierają szybę w jej płaszczyźnie i mają charakter punktowy, a listwy dociskowe są liniowymi podporami umieszczonymi na obwodzie szyby i zapobiegają przesunięciu szyby w płaszczyźnie prostopadłej do ściany osłonowej.
W praktyce inżynierskiej często upraszcza się wspomniane wyżej sposoby podparcia do podpór przegubowo-nieprzesuwnych czyli takich, w których przesuw jest zablokowany we wszystkich trzech kierunkach.
Przy typowych wymiarach szyb (o pow. do ok. 2 m2) i niewielkich ugięciach dostatecznie dobre wyniki dają liniowe metody obliczeń, co zostanie przedstawione w niniejszym artykule.
Przyjmuje się, że liniowe metody obliczeń (popularne metody inżynierskie) mogą być stosowane w przypadku ugięć nie przekraczających grubości pojedynczej tafli szkła. Przy takich założeniach nie ma znaczenia, jaki typ podpory (przegubowo-przesuwnej czy przegubowo-nieprzesuwnej) został przyjęty w modelu, gdyż wyniki obliczeń są identyczne w obu przypadkach podparcia. Z reguły przy takich obliczeniach podaje się informację, że jest to podparcie przegubowe, co w zupełności jest wystarczające do rozwiązania zadania.
Inaczej powinno się traktować wpływ rodzaju podpór w modelu na wyniki obliczeń dla szyb wielkoformatowych (np. o wymiaracg 2,0x2,0 m). W takich przypadkach, w zależności od wartości obciążenia, mogą i zazwyczaj występują przy ugięciach większych od grubości tafli szkła, wyraźne nieliniowości modelu. Ścisłe rozwiązania analityczne modeli nieliniowych są dosyć skomplikowane, a przy złożonych warunkach podparcia używa się przybliżonych metod rozwiązania (np. metody Ritza lub Galernika [1]) lub metod numerycznych metody elementów skończonych (MES).
Wpływ na wynik obliczeń sposobu analizy (liniowy, nieliniowy) oraz warunków podparcia, został przedstawiony na prezentowanych niżej przykładach. Obliczenia przeprowadzono dla pojedynczej szyby (litej tafli szkła). Przykład 1 dotyczy oszklenia wielkoformatowego (2,0x2,0 m), przykład 2 oszklenia typowego (1,0x1,0 m) przy tej samej grubości szyby tj.10 mm.
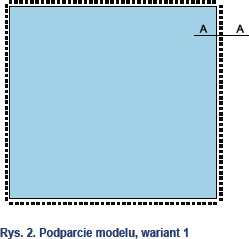
Przykład1
Do obliczeń przyjęto pojedynczą taflę szkła grubości 10 mm o wymiarach 2,0x2,0 m, w dwóch wariantach podparcia:
- wariant 1 – podparcie przegubowo-nieprzesuwne na obwodzie modelu, rys. 2,
- wariant 2 – podparcie przegubowo-przesuwne na obwodzie modelu, z możliwością przesuwu w płaszczyźnie szkła (odwzorowanie listwy dociskowej) oraz podparcie punktowe przegubowo-przesuwne i przegubowo nieprzesuwne umieszczone 150 mm od naroży oszklenia, podpierające model na dolnej krawędzi (odwzorowanie podkładek podpierających), rys. 3.
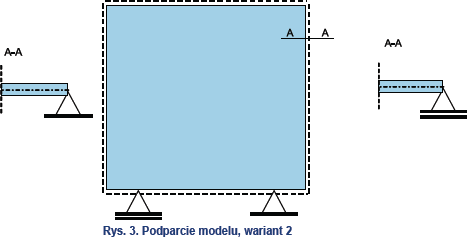
Do modelu przykładane są obciążenia równomiernie rozłożone, o wartości od 100 Pa do 2000 Pa.
Dla dwóch wariantów podparcia i narastającym obciążeniu, przeprowadzono dwa rodzaje analizy: liniową i nieliniową. Obliczenia wykonano metodą elementów skończonych (MES). Wynikiem obliczeń są maksymalne ugięcia modelu (w środku rozpiętości) w zależności od rodzaju podparcia i sposobu analizy.
Wyniki obliczeń zestawiono w tablicy 1 i na wykresie 1.
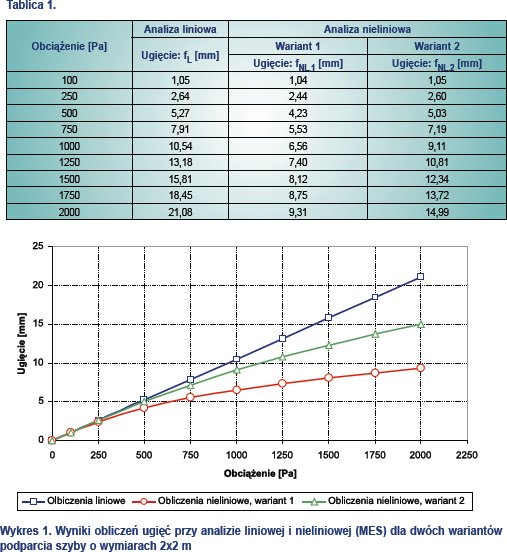
Przy niewielkich obciążeniach (250 Pa) wyniki obliczeń liniowych i nieliniowych są zbieżne (tablica 1, wykres 1), dalej widoczne są wyraźnie różnice wyników obliczeń pomiędzy analizą liniową i nieliniową, a co ważniejsze, różnice występują również pomiędzy wynikami analizy nieliniowej dla tego samego modelu z różnymi wariantami podparcia.
Przy niewielkich obciążeniach (do 250 Pa) największa różnica wyników obliczeń (pomiędzy modelem liniowym i nieliniowym z 1 wariantem podparcia) nie przekracza 10%. Przy narastającym obciążeniu wyniki obliczeń modeli nieliniowych coraz bardziej odbiegają od modelu liniowego, ale również wyniki obliczeń spowodowane przyjęciem różnych wariantów podparcia w analizie nieliniowej znacznie się od siebie różnią, aby ostatecznie (przy obciążeniu 2000 Pa) dojść do poziomu około 60%.
Jeśli wykluczy się z obliczeń model liniowy, to i tak przy większych obciążeniach modele nieliniowe przy różnych warunkach podparcia nie są spójne. Zatem przy obliczaniu ugięć szyb wielkoformatowych, oprócz przyjęcia analizy nieliniowej, szczególną uwagę należy zwrócić na poprawne przyjęcie warunków podparcia.
W omawianym przypadku pierwszy wariant podparcia tafli szkła (przegubowo-nieprzesuwne na obwodzie, rys. 2 ), jest podparciem znacznie uproszczonym w odniesieniu do rzeczywistej konstrukcji, gdyż, jak wynika z opisu zamieszczonego wcześniej, mocowania szyby w konstrukcji nośnej słupowo-ryglowej, podparcie przegubowo-nieprzesuwne właściwie nie występuje.
Warto jednak wspomnieć o takim podparciu dlatego, że jest to najczęściej przyjmowany sposób podparcia w tzw. w obliczeniach inżynierskich, z uwagi na możliwości obliczania nawet bez stosowania metod numerycznych.
Drugi wariant podparcia (podparcie przegubowo-przesuwne na obwodzie modelu i podparcie przegubowe punktowe w dwóch miejscach na dolnej krawędzi tafli szkła, rys. 3) znacznie lepiej odwzorowuje rzeczywiste podparcie, natomiast bardzo komplikuje opis matematyczny w metodzie Ritza lub Galernika i bez zastosowania odpowiednich metod numerycznych z możliwością analizy nieliniowej, zadanie może być trudne do rozwiązania.
Przykład 2
Do obliczeń przyjęto pojedynczą taflę szkła grubości 10 mm, o wymiarach 1,0x1,0 mm. Obliczenia wykonano dla zakresu obciążeń (od 100 Pa do 2000 Pa), metody analizy (liniowa, nieliniowa) oraz w wariantach podparcia – analogicznie, jak w przykładzie 1. Obliczenia wykonano metodą elementów skończonych (MES).
Uwaga: w celu porównania wpływu warunków podparcia w zależności od wymiarów szyby na wyniki obliczeń przyjęto (jak już wspomniano wcześniej), że grubość szyby jest taka sama jak w przykładzie 1. Przy innej, tj. mniejszej grubości szyby dla wymiarów 1x1 m, będą występowały nieliniowości ugięcia w zależności od obciążenia.
Wyniki obliczeń zestawiono w tablicy 2 i wykresie 2.
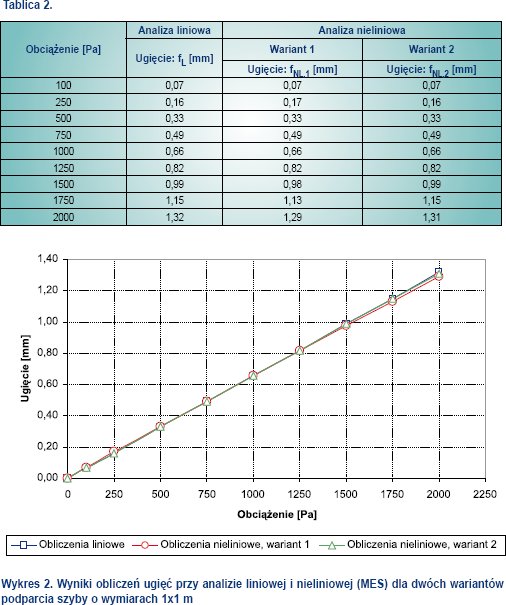
Wyniki obliczeń dotyczące szyby o wymiarach 1,0x1,0 m jednoznacznie wskazują na to, że w przypadku szyb o typowych wymiarach, nie ma większego znaczenia sposób analizy (liniowa lub nieliniowa) ani sposób podparcia (podpory przegubowe lub podpory przegubowo-przesuwne z dwoma podparciami punktowymi), gdyż wyniki tych obliczeń są w zasadzie identyczne.
Maksymalna rozbieżność wyników obliczeń to około 2% przy maksymalnym obciążeniu, w porównaniu analizy liniowej z analizą nieliniową. Niżej wykonano obliczenia sprawdzające metodą inżynierską dla maksymalnego obciążenia tj. 2,0 kPa.
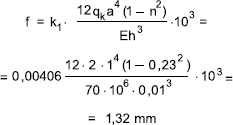
gdzie:
f – maksymalne ugięcie [mm],
k1=0,00406 – współczynnik zależny od stosunków boku szyby (a/b),
E=70 x 106 kPa – moduł sprężystości podłużnej szkła,
v=0,23 – współczynnik Poissona dla szkła,
q = 2,0 kPa – obciążenie,
a=1,0 m – długość boku szyb,
h = 0,01 m – grubość szyby.
Wynik obliczeń inżynierskich oczywiście potwierdza wynik obliczeń numerycznych dla analizy liniowej (patrz tablica 2).
Przy niewielkich odkształceniach i typowych wymiarach szyb, analizy liniowe z podparciem przegubowym są dostatecznie dokładne, aby można było je wykorzystywać w praktyce.
Przy projektowaniu oszkleń wielkoformatowych i dużych ugięciach, istotne znaczenie ma wykorzystywanie dostosowanych (do analizy takich elementów) metod obliczeń zwłaszcza nieliniowych oraz przyjęcie warunków podparcia możliwie najbardziej zbliżonych do rzeczywistej konstrukcji.
Większość tego typu obliczeń możliwa jest do realizacji (z uwagi na złożoność zadania) przy wykorzystaniu numerycznych metod obliczeń, np. metoda elementów skończonych (MES).
W następnym artykule zostanie przedstawiony przykład obliczeń ugięć wielkoformatowej szyby zespolonej z uwzględnieniem wpływu warunków podparcia w porównaniu z wynikami badań.
Instytut Techniki Budowlanej
Wykorzystane materiały.
[1] M. Bijak-Żachowski, Mechanika materiałów i konstrukcji. Tom 2. Warszawa 2006. Oficyna wydawnicza Politechniki Warszawskiej.
inne artykuły tego autora:
- Projektowanie bezpiecznych przeszkleń w ścianach osłonowych ze szkłem , Artur Piekarczuk, Świat Szkła 2/2010
- Weryfikacja badawcza numerycznych metod obliczeń szyb zespolonych , Artur Piekarczuk, Świat Szkła 10/2008
- Wpływ warunków podparcia na wyniki obliczeń ugięć szyb wielkoformatowych pod obciążeniem równomiernie rozłożonym, Artur Piekarczuk, Świat Szkła 4/2008
- Metoda projektowania szyb zespolonych, Artur Piekarczuk, Świat Szkła 3/2008
- Metoda obliczeń ugięć okien PVC pod obciążeniem wiatrem , Artur Piekarczuk, Świat Szkła 7-8/2006
- Ściany osłonowe z oszkleniem mocowanym mechanicznie Cz. 2, Artur Piekarczuk, Świat Szkła 6/2005
- Ściany osłonowe z oszkleniem mocowanym mechanicznie Cz. 1, Artur Piekarczuk, Świat Szkła 5/2005
patrz też:
- Modelowanie obciążeń klimatycznych szyb zespolonych. Część 2 , Zbigniew Respondek, Świat Szkła 1/2005
- Modelowanie obciążeń klimatycznych szyb zespolonych. Część 1 , Zbigniew Respondek, Świat Szkła 12/2004































