Artykuł prezentuje porównanie wyników numerycznych i analitycznych metod analizy zespolonych dwuteowych belek drewniano-szklanych z przeprowadzonymi badaniami eksperymentalnymi.
Główny nacisk położono na analizę rozkładu naprężeń normalnych do przekroju poprzecznego poszczególnych elementów składowych belek. W pierwszej części artykułu przeprowadzono syntetyczne zestawienie badań eksperymentalnych oraz analiz numerycznych belki zespolonej drewniano-szklanej wraz z podaniem założeń.
W kolejnej części artykułu przeprowadzono analizę analityczną dostępnymi w literaturze metodami. Porównanie wyników analiz i badań eksperymentalnych przeprowadzono w celu pokazania różnic między metodami analitycznymi oraz wskazania projektantom drogi świadomego wyboru.
Wstęp
Szkło wykorzystywane jest w budownictwie od stuleci, ale dopiero od niedawna rozwijane są techniki analiz tego materiału pozwalające na wykorzystanie tego materiału do celów konstrukcyjnych. W związku z rosnącą popularnością szkła w budownictwie, w literaturze można znaleźć coraz więcej badań wszelkiego rodzaju konstrukcyjnych elementów szklanych, najczęściej w zespoleniu z innymi materiałami. Jednym z typów takich elementów sa dwuteowe belki zespolone drewniano-szklane, w których zespolenie odbywa się przez warstwę kleju elastycznego (rys. 1).
Jest to tendencja o tyle zrozumiała, że dla użytkowników oraz architektów przeźroczyste elementy nośne nadają obiektom budowlanym lekkości i efektownego wyglądu. Belki zespolone drewniano-szklane pozwalają wykorzystać najsilniejsze cechy obu materiałów. W przypadku szkła jest to sztywność i duża wytrzymałość na ściskanie, natomiast w przypadku drewna duża ciągliwość, zdolność do uplastycznienia i łatwość obróbki. Powstałe w ten sposób elementy konstrukcyjne charakteryzują się znaczną nośnością pokrytyczną [1–13], tj. wartością nośności elementu po pojawieniu się pierwszych rys w szklanym środniku.

Rys. 1. Belka wykonana na potrzeby badań eksperymentalnych
Zachowanie elementu zespolonego, w którym zespolenie odbywa się przez warstwę elastycznego spoiwa nie może być analizowane przy założeniu pełnego zespolenia elementów składowych, tak jak pozwala to czynić norma PN-EN 1994-1-1 [14] dla zespolonych elementów stalowo-betonowych. Nawet przy zapewnieniu nośności spoiny klejowej dla elementu w pełni zespolonego musimy liczyć się w tym przypadku z pewnym poślizgiem w połączeniu.
Poślizg ten będzie generował wzrost naprężeń w środniku szklanym co jest zjawiskiem wysoce niebezpiecznym ze względu na brak zdolności szkła do jakiegokolwiek uplastycznienia miejscowego. Ponadto, przeprowadzone analizy numeryczne belki poddanej czteropunktowemu zginaniu wskazują, że mimo iż moment globalny między siłownikami ma stałą wartość, to rozkład maksymalnych naprężeń normalnych na tym odcinku nie jest stały.
Metody analizy belek
Analizę nośności na zginanie dwuteowych belek zespolonych drewniano-szklanych można przeprowadzić jedną z 3 metod:
- Analizy numeryczne (Metoda Elementów Skończonych);
- Analiza analityczna belek złożonych zaproponowana w normie PN-EN 1995-1-1 (metoda γ) [15];
- Analiza analityczna belek złożonych zaproponowana przez Pischla [16].
Pierwsza ze wspomnianych metod, najbardziej ogólna, pozwala – przy znajomości parametrów poszczególnych materiałów – przeanalizować zachowanie elementu zespolonego. Ze względu na dużą czasochłonność metody można przypuszczać, że nie znajdzie zastosowania w praktyce projektowej. Pierwsza z metod analitycznych, znana jako metoda γ, została zaproponowana przez Karla Möhlera do projektowania belek drewnianych złożonych, w których części połączono podatnie za pomocą łączników mechanicznych [15]. Ideą tego podejścia jest uzależnienie rozkładu naprężeń w częściach składowych belki zespolonej jedynie od sztywności połączenia między nimi.
Metoda została adaptowana dla zespolonych belek drewniano-szklanych [17] oraz zespolonych belek stalowo-szklanych [18]. Dla badanych przez innych autorów zespolonych belek drewniano- szklanych uzyskano bardzo dobre zgodności wyników metody z badaniami eksperymentalnymi [17, 19], natomiast dla badanych belek stalowo-szklanych zgodność ta była nieco gorsza [18]. W pracy Metody analityczne projektowania belek zespolonych drewniano-szklanych („Przegląd Budowlany” 2016) [20] przeprowadzono analizę zgodności metody γ z wynikami obliczeń numerycznych wolnopodpartych belek zespolonych drewniano-szklanych przy różnych schematach obciążenia.
Analizy pokazały, że metoda cechuje się zadowalającą zgodnością wyników analitycznych z numerycznymi dla belek obciążonych w sposób ciągły, natomiast w przypadku obciążeń skupionych wartości naprężeń maksymalnych w środniku są znacznie zaniżone [20]. Niniejszy artykuł stanowi rozszerzenie tej pracy [20], dlatego też specyfika rozpatrywanego problemu oraz opis analiz numerycznych potraktowano tu skrótowo.
Ponadto, dla zachowania lepszej przejrzystości artykułu, zdecydowano się również na skrócony opis badań eksperymentalnych, a dokładne ich przedstawienie znaleźć można w pracach Capacity of composite timber- glass beams subjected to multiple variable loading (Cracow University of Technology, 2017) [12] i The load-bearing capacity of timber-glass composite I-beams made with polyurethane adhesives (Zielona Góra, 2017) [13].
(...)
Badania eksperymentalne
Na rys. 2 przedstawiono przekrój belki wykorzystanej w badaniach wraz z wymiarami elementów. Przygotowano 6 belek, wszystkie o wymiarach 3100x220x70 mm. Pasy wykonano z drewna litego jodłowego klasy C22, o wymiarze przekroju poprzecznego 40x70 mm, z przygotowanym rowkiem na wklejenie szklanego środnika o wymiarach 17x10,68 mm. Drewno do wykonania pasów zostało starannie wyselekcjonowane i tak dobrane, aby było częścią twardzieli, co zapewnia stałość wymiarów przy zmieniającej się wilgotności i bardzo małą ilość sęków. Do konstrukcji środnika belek wykorzystanych w badaniach zdecydowano się użyć szkło laminowane typu float (annealed) na folii PVB. Środnik składa się z dwóch szyb o wymiarach przekroju 3x170 mm każda, sklejonych podwójną warstwą folii PVB, co łącznie daje wymiar przekroju środnika równy 6,68x170 mm. Dodatkowo, w przypadku szyb szklanych zginanych względem osi o większym momencie bezwładności, bardzo ważne jest odpowiednie przygotowanie krawędzi, które zostały wypolerowane zgodnie z normą ISO 12543-1:2011(E) [21]. Do połączenia pasów i środnika wybrano klej poliuretanowy Sika®PS, charakteryzujący się bardzo dobrą przyczepnością do powierzchni szklanej i drewnianej, odpornością na działanie podwyższonej temperatury, dobrą sztywnością postaciową, odpornością na działanie promieni UV oraz dużą wartością wytrzymałości na rozciąganie i ścinanie.
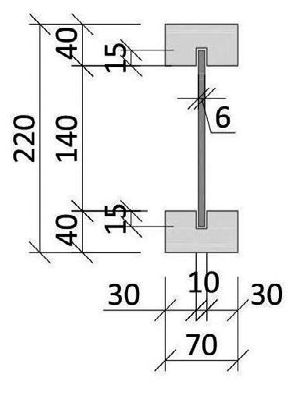
Rys. 2. Przekrój belki zespolonej drewniano-szklanej poddanej analizie
Badania czteropunktowego quasi-statycznego zginania 3 belek przeprowadzono w Laboratorium Materiałów i Konstrukcji Budowlanych Politechniki Krakowskiej. Na rys. 3 przedstawiono schemat stanowiska badawczego.
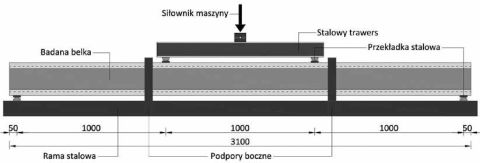
Rys. 3. Schemat stanowiska badawczego do badania belek
Analizy numeryczne
Analizy numeryczne zostały przeprowadzone na identycznym układzie stanowiska, jak badania eksperymentalne. Model numeryczny belki został zbudowany jako model przestrzenny o rzeczywistych wymiarach wszystkich elementów składowych. Wielkość zastosowanego elementu skończonego dla pasów oraz środnika szklanego to 5 mm, natomiast dla 2 mm warstwy kleju – 2 mm (Rys. 4). Użyto elementów izometrycznych sześciennych o 20 węzłach z hybrydowym sformułowaniem równań wewnątrz elementu skończonego. Układ został obciążony dwiema siłami skupionymi o wartościach 2,25 kN każda. Ze względu na podwójną symetrię układu analizie numerycznej poddano jedynie ćwiartkę modelu przy założeniu odpowiednich więzów odwzorowujących symetrię układu.

Rys. 4. Widok modelu numerycznego belki
Po przeprowadzeniu analizy numerycznej belki zginanej zaobserwowano, że mimo iż moment globalny między siłownikami ma stałą wartość, to rozkład naprężeń normalnych na tym odcinku nie jest stały (Rys. 5). Na mapie naprężeń widać, że największa koncentracja, a co za tym idzie, maksymalne naprężenia normalne nie są stałe na odcinku stałego momentu globalnego. Maksymalne naprężenie wyniosło dla badanego przypadku 31 MPa (wartości odczytana w punktach Gaussa a następnie ekstrapolowana do krawędzi środnika). Lokalną koncentrację naprężeń normalnych w środniku belek zespolonych drewniano-szklanych poddanych zginaniu czteropunktowemu potwierdzają również badania eksperymentalne takich elementów opisane w literaturze [12, 13, 17, 22, 23]. We wszystkich wspomnianych badaniach pierwsze rysy w szklanych środnikach pojawiały się zawsze pod którymś z siłowników po stronie włókien rozciąganych.

Rys. 5. Naprężenia normalne do przekroju poprzecznego belki
Wyniki, dyskusja wyników
Dla zobrazowania różnic między metodami analitycznymi oraz ich zgodności zarówno z badaniami eksperymentalnymi, jak i z analizami numerycznymi przedstawiono rozkłady sił wewnętrznych dla zespolonej belki drewniano-szklanej o wymiarach jak na rys 2. Przyjęto identyczny schemat statyczny oraz konfigurację obciążenia jak podczas badań belki (Rys. 3). Jako obciążenie przyjęto stałe obciążenie skupione w postaci dwóch sił o wartości stałej dla wszystkich porównywanych elementów równej 4.5 kN na dwóch siłownikach łącznie.
Na wykresach (Rys. 6 i Rys. 7) przedstawiono zestawienie wyników przeprowadzonych analiz. Na Rys. 6 zaprezentowano wykresy momentów zginających oraz siły rozciągającej dolny pas belki. Zrezygnowano z prezentacji wykresów dla pasa ściskanego ze względu na symetryczną konstrukcję belki. Przebiegi i wartości dla poszczególnych metod są zbliżone do siebie, szczególnie w przypadku metody Pischla oraz modelu numerycznego belki. Dla tych dwóch modeli zaobserwować można niemal idealną zgodność przebiegu siły osiowej i momentu zginającego, które różnią się jedynie w miejscu przyłożenia obciążenia. Warto zwrócić uwagę, że różnica ta wynika z bardziej dokładnego odwzorowania, a przez to również „wygładzenia” wykresu w przypadku modelu numerycznego. Niemniej jednak, przeszacowanie wartości maksymalnych sił i momentów w przypadku metody Pischla nie stwarza niebezpieczeństwa awarii konstrukcji.
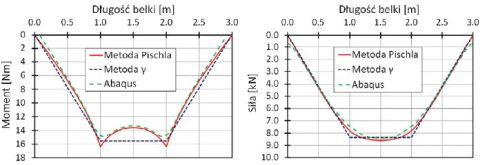
Rys. 6. Wykres momentu zginającego (po lewej) i siły rozciągającej (po prawej) dolny pas belki
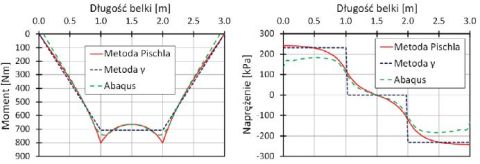
Rys. 7. Wykres momentu zginającego szklany środnik belki (po lewej) oraz wykres naprężeń ścinających spoinę klejową (po prawej)
Podobnie, jak w przypadku pasów drewnianych, wykresy momentu zginającego w środniku (Rys. 7), a więc w najbardziej newralgicznej części konstrukcji, różnią się w nieznacznym stopniu między sobą. Najniekorzystniej – w porównaniu z pozostałymi metodami – wypada tutaj metoda γ, która ze względu na brak zależności wartości sił przekrojowych od schematu obciążenia, zaniża wartości maksymalnych momentów w miejscach przyłożenia obciążenia. Badania prowadzone na potrzeby niniejszej pracy, jak i badania dostępne w literaturze wskazują, że maksymalne naprężenia rozciągające szkło pojawiają się właśnie pod miejscami przyłożenia obciążenia i to tam pojawia się pierwsza rysa. Prowadzi to do wniosku, że zarówno wartości sił przekrojowych otrzymane metodą Pischla oraz z analizy numerycznej są najbardziej zbieżne z wynikami badań. Podobnie, jak w przypadku momentu zginającego pas drewniany, tutaj również zauważyć można wygładzenie wykresu przypadku modelu numerycznego oraz przeszacowanie wartości maksymalnej momentu w przypadku metody Pischla.
Na wykresie naprężeń ścinających spoinę po długości elementu również uwidacznia się znaczna zbieżność między analizami numerycznymi oraz wynikami otrzymanymi z analizy metodą Pischla. W przypadku metody γ, naprężenie ścinające jest jedynie zależne od globalnej postaci siły ścinającej, co daje wykres naprężeń ścinających jak dla belki w pełni zespolonej. Skończona sztywność połączenia między pasami, a środnikiem sugeruje jednak, że naprężenia ścinające powinny rozkładać się nieco bardziej płynnie po długości belki, niż wynika to z rozkładu siły ścinającej dla rozpatrywanego schematu statycznego belki. Przebiegi naprężeń ścinających spoinę otrzymane z analizy numerycznej oraz wyznaczone metodą Pischla wskazują na wyższość tych metod również w tym przypadku.
Dla porównania przeprowadzonych analiz analitycznych i numerycznych, na wykresach (Rys. 8 i Rys. 9) przedstawiono przebiegi naprężeń normalnych do przekroju pod miejscem przyłożenia siły. Wyznaczone rozkłady naprężeń metodami analitycznymi oraz numerycznymi zostały odniesione do wartości zmierzonych bezpośrednio w trakcie badań belek poddanych jedynie obciążeniu quasi-statycznemu (Rys. 8) oraz belek poddanych obciążeniu wielokrotnie zmiennemu a następnie quasi-statycznemu (Rys. 9). Oba wykresy pokazują, że wszystkie analizowane metody przewidywania wartości naprężeń w przekroju zespolonym dają zadowalające zgodności z eksperymentem. Wartości naprężeń oszacowane zarówno metodami analitycznymi jak i numerycznymi w każdym przypadku są większe od wartości uzyskanych w badaniach. Wartości zarówno naprężeń, jak i ugięć badanych elementów zostały odczytane dokładnie dla takiego samego poziomu obciążenia jak przyjęto do analizy, tj. 4.5 kN.
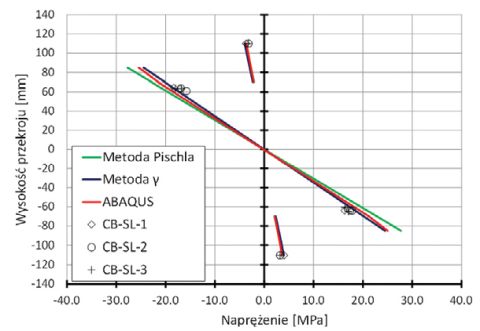
Rys. 8. Naprężenia w przekroju pod siłownikiem wyznaczone w oparciu o metody analityczne (Metoda Pischla i Metoda Gamma), numeryczne (ABAQUS) oraz zmierzone w trakcie badań elementów poddanych jedynie obciążeniu quasi-statycznemu
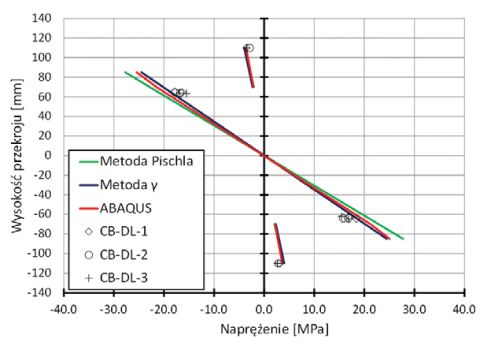
Rys. 9. Naprężenia w przekroju pod siłownikiem wyznaczone w oparciu o metody analityczne (Metoda Pischla i Metoda Gamma), numeryczne (ABAQUS) oraz zmierzone w trakcie badań elementów poddanych obciążeniu wielokrotnie zmiennemu oraz quasi-statycznemu
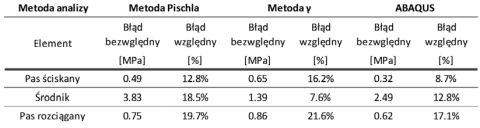
W tablicy 1 przedstawiono średnie wartości błędów bezwzględnych oraz względnych w odniesieniu do wyników badań eksperymentalnych. Przytoczone porównanie wskazuje, że wszystkie zastosowane metody znacznie odbiegają od wartości wynikających z badań, w skrajnych przypadkach przeszacowując wartości naprężeń o 21,6%. Ze względu na dużą zgodność między wynikami analiz numerycznych i analitycznych, należy jednak sądzić, że otrzymane rozbieżności między analizami a badaniami eksperymentalnymi mogą wynikać ze znacznej zmienności parametrów drewna czy spoiny klejowej. Niemniej jednak, mimo znacznych rozbieżności między badaniami a wynikami analiz numerycznych i analitycznych, należy zwrócić uwagę na przeszacowanie wartości naprężeń w drewnie i szkle w przypadku wszystkich trzech dostępnych metod analizy. Daje to pewien zapas bezpieczeństwa w przypadku analizy belek przedstawionych w pracy.
Tablica 1. Porównanie metod analitycznych i numerycznych z wynikiem eksperymentu
Przebieg sił i momentów przekrojowych w belce wskazuje, że z dwóch metod analitycznych, to metoda Pischla nieco lepiej oddaje rzeczywisty rozkład tych wielkości w belce. Analizując rozbieżności między wartościami naprężeń otrzymanych w trakcie badań z tymi uzyskanymi w trakcie analiz dochodzimy jednak do wniosku, że najdokładniej wartości naprężeń opisuje metoda γ, szczególnie w przypadku szkła. Dla kompletnego porównania metod analitycznych z metodami numerycznymi i wynikami badań eksperymentalnych słuszne wydaje się porównanie ugięć elementów zginanych. Ugięcie średnie badanych belek zespolonych przy obciążeniu równym 4,5 kN wyniosło 3,94 mm, a ugięcie wyznaczone dla identycznie obciążonej belki w przestrzennym modelu numerycznym wyniosło 4,17 mm. Z uwagi na postać metody Pischla i brak jawnej postaci sztywności giętnej elementu, analitycznie wyznaczono ugięcie na podstawie sztywności wyznaczonej metodą γ, które wyniosło 3,98 mm. Jak widać, mimo dużych rozbieżność w przewidywanych wartościach naprężeń, różnica między ugięciem wyznaczonym analitycznie i numerycznie, a wartością uzyskaną w trakcie badań doświadczalnych wyniosła 5.8% błędu względnego.
Wnioski
Zarówno zaprezentowane metody analityczne, jak i numeryczne analizy zespolonych belek drewniano- szklanych, pozwoliły uzyskać dobrą zgodność wartości naprężeń z wartościami uzyskanymi w trakcie badań. Nieco lepszą dokładność wyników uzyskano metodą Pischla. Jak pokazano w przywoływanej wcześniej pracy [20], dokładność tej metody względem modelu numerycznego wynosi ok. 2,5% dla obciążenia w postaci dwóch sił skupionych. Dla tych samych przypadków obciążeniowych naprężenia wyznaczone metodą γ okazały się niedoszacowane dla obciążenia siłami skupionymi (błąd ok. 7%).
W odniesieniu do badań eksperymentalnych nie udało się uzyskać zadowalających zgodności wyników estymacji analitycznych czy numerycznych z wynikami tych badań. Rozbieżności w szacowaniu naprężeń dochodzące do 21,6% mogły być spowodowane nieco innymi parametrami drewna niż te, które uzyskano z badań tego materiału lub nieco innego niż przewidywano zachowania spoiny klejowej. Spoina klejowa w przypadku belek zespolonych o badanej konstrukcji pracuje w bardzo skrępowanych warunkach i mogło się to przyczynić do jej „usztywnienia” w trakcie badania. Niemniej jednak, należy zwrócić uwagę na uzyskaną bardzo dobrą zgodność ugięcia oszacowanego zarówno metodą analityczną, jak i numeryczną, ze średnim ugięciem belek w trakcie badań.
Metoda γ, ze względu na prostotę znalazła dotychczas szersze zastosowanie w projektowaniu belek złożonych, a jej interpretacja pojawiła się również w normie Eurokod 5 [15]. Autor uważa, że metoda ta jest odpowiednia do analizy belek zespolonych drewniano-szklanych obciążonych w sposób równomierny. Mimo dużej wartości materiałowego współczynnika bezpieczeństwa dla szkła (wg nowej instrukcji Komisji Europejskiej wynosi 1.8) [24], elementy obciążone punktowo zaleca się poddać dokładniejszej analizie, ze względu na możliwość pojawienia się lokalnych konsternacji naprężeń rozciągających w szkle, szczególnie niebezpiecznych dla tego materiału.
Konrad Rodacki
Małgorzata Mieszczak
LITERATURA
[1] K. Kreher: Load introduction with timber. Timber as reinforcement for glued composites (shear-walls, I-beams) structural safety and calculation-model, in: Portland, 2006.
[2] J. Hamm: Development of timber-glass prefabricated structural elements, in: Lahti, 2001: pp. 41–46.
[3] P. Cruz, J. Pequeno: Timber-glass composite beams: Mechanical behaviour and architectural solutions, in: Delft, 2008: pp. 439–449.
[4] L. Blyberg, M. Lang, K. Lundstedt, M. Schander, E. Serrano, M. Silfverhielm, C. Stälhandske: Glass, timber and adhesive joints - Innovative load bearing building components, Construction and Building Materials. (2014) 470–478.
[5] L. Blyberg, E. Serrano, B. Enquist, M. Sterley: Adhesive joints for structural timber/glass applications: Experimental testing and evaluation methods, International Journal of Adhesion & Adhesives. (2012) 76–87.
[6] L. Blyberg, E. Serrano: Timber/Glass adhesively bonded I-beams, (n.d.).
[7] M. Kozłowski: Experimental and numerical analysis of hybrid timber-glass beams, Rozprawa doktorska, Politechnika Śląska, 2014.
[8] M. Kozłowski, J. Hulimka: Load-bearing capacity of hybrid timber-glass beams, ACEE Journal. (2014) 61–70.
[9] M. Dorn, M. Kozłowski, E. Serrano: Design approaches for timber-glass beams, in: Dusseldorf, 2014: pp. 1–9.
[10] J. Hulimka, M. Kozłowski: Mechanism of failure and post-breakage strength of hybrid timber-glass beams, in: Slovak Society of mechanics SAS, Bratysława, 2012.
[11] M. Premrov, M. Zlatinek, A. Štrukelj: Experimental analysis of load-bearing timber-glass I-beam, Construction of Unique Buildings and Structures. (2014) 11–20.
[12] K. Rodacki: Capacity of composite timber-glass beams subjected to multiple variable loading, PhD Thesis, Cracow University of Technology, 2017.
[13] K. Rodacki: The load-bearing capacity of timber-glass composite I-beams made with polyurethane adhesives, in: XI Konferencja Konstrukcje Zespolone, Zielona Góra, 2017.
[14] PN-E 1994-1-1 Projektowanie zespolonych konstrukcji stalowo-betonowych. Część 1-1: Reguły ogólne i reguły dla budynków, PKN, 2008.
[15] PN-EN 1995-1-1: 2010 Eurokod 5. Projektowanie konstrukcji drewnianych. Cześć 1-1: Postanowienia ogólne. Reguły ogólne i reguły dotyczące budynków, PKN, 2010.
[16] R. Pischl: Die Berechnung Zusammengesetzter Holzerner Biegetrager auf Grund der Elastischen Verbundtheorie, Rozprawa doktorska, Technischen Hochschule Graz, 1966.
[17] M. Kozłowski: Experimental and numerical analysis of hybrid timber-glass beams, Rozprawa doktorska, Politechnika Śląska, 2014.
[18] D. Ungermann, E. Preckwinkel: Structural behaviour of hybrid steel-glass beams., in: TU Delft, Maj 20110: pp. 485–495.
[19] M. Kozłowski: Hybrid glass beams. Review of research projects and applications, ACEE Journal. (2012).
[20] K. Rodacki, K. Furtak: Metody analityczne projektowania belek zespolonych drewniano-szklanych, „Przegląd Budowlany” (2016) 24–31.
[21] ISO 12543-1:2011(E) Szkło w budownictwie. Szkło warstwowe i bezpieczne szkło warstwowe. Część 1: Definicja i opis elementów składowych, 2011.
[22] M. Kozłowski, E. Serrano, B. Enquist: Experimental investigation on timber-glass composite I-beams, in: Taylor & Francis Group, Londyn, 2014.
[23] L. Blyberg, E. Serrano: Timber/Glass adhesively bonded I-beams, (n.d.).
[24] M. Feldmann, R. Kasper, eds.: Guidance for European Structural Design of Glass Components. Support to the implementation, harmonization and further development of the Eurocodes, Publications Office of the European Unio, Luxemburg, 2014.
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 11/2017









































