Wielkoformatowe, szklane ściany osłonowe na stałe wpisały się w trendy nowoczesnej architektury. Powierzchnia jednej tafli, często przekraczająca 8 m2, sprawia, że używanie ich w przypadku liniowych metod obliczeń, szeroko stosowanych dla szyb typowych, prowadzi do znacznego przeszacowania wartości ugięć. Oprócz wyboru odpowiedniej metody obliczeń bardzo ważne jest także przyjęcie odpowiedniego schematu statycznego pracy szyby. W standardowych rozwiązaniach szyba podparta jest liniowo po obwodzie lub za pomocą mocowań punktowych. Zarówno w pierwszym, jak i drugim przypadku są to podpory przesuwne.
Wprowadzenie
Takie rozwiązanie jest zdeterminowane dużą wrażliwością szkła na lokalne koncentracje naprężeń, często będące efektem odkształceń termicznych. Przyjęcie nieprawdziwego (nieprzesuwnego) sposobu podparcia prowadzi do znacznego niedoszacowania wartości ugięć. Praca przedstawia analizę rozrzutu wyników ugięć, wyznaczonych w zależności od rodzaju analizy oraz schematu statycznego szklanych ścian osłonowych. Artykuł powstał na podstawie publikacji Wpływ metody obliczeń oraz schematu podparcia na ugięcia wielkoformatowych szklanych ścian osłonowych, zaprezentowanej przez autora na XIII Konferencji Naukowej Doktorantów Wydziałów Budownictwa w Szczyrku, w 2013 r.
Nieliniowość geometryczna szklanych tafli
W przeciwieństwie do innych elementów budowlanych, szklane tafle doznają znacznych ugięć przed utratą nośności. Analizując zachowanie się szklanej tafli o niewielkiej grubości, obciążonej w sposób równomiernie rozłożony i podpartej w sposób nieprzesuwny wzdłuż wszystkich krawędzi, można zauważyć, że duże deformacje (ugięcia) skutkują powstaniem rozciągających naprężeń błonowych, które powodują wzrost sztywności tej płyty. Rys. 1 przedstawia ugięcia szklanej tafli (wzdłuż przekątnej) obciążonej równomiernie w zakresie obciążeń od 1000 do 7000 N/m2. Można zauważyć, że wraz ze wzrostem obciążenia, przyrost ugięć maleje, co jest spowodowane zmianą sztywności płyty.
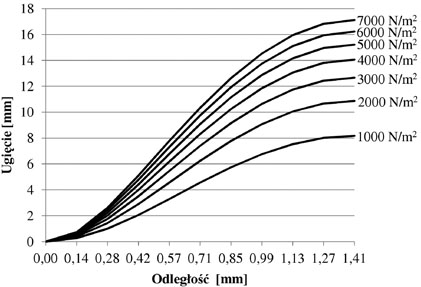
Rys. 1. Ugięcie szklanej tafli (wzdłuż przekątnej) o wymiarach 2000x2000 mm i grubości 8 mm przy analizie nieliniowej
Wzrost sztywności płyty wystąpi również w sytuacji, w której jest ona podparta w sposób przesuwny. Duże ugięcia powodują powstanie w tafli ściskających naprężeń obwodowych oraz naprężeń rozciągających w części środkowej. W takich przypadkach założenia teorii płyt Kirchhoffa nie są spełnione, a do opisania nieliniowości geometrycznej należy stosować złożone równania von Karmana, uwzględniające powstanie naprężeń błonowych. Analityczne rozwiązanie tych równań, szczególnie w przypadku złożonych warunków podparcia, jest bardzo skomplikowane i trudne do stosowania w praktyce inżynierskiej. Z tego powodu najczęściej są wykorzystywane numeryczne metody obliczeniowe, np. metoda elementów skończonych (MES).
(...)
Analizy numeryczne
Pierwsza analiza dotyczy szacowania ugięć kwadratowych szyb poddanych równomiernemu obciążeniu powierzchniowemu. Do obliczeń przyjęto pojedyncze, kwadratowe tafle szkła o wymiarach boku 1000, 1500 oraz 2000 mm, podparte w sposób przegubowo-przesuwny wzdłuż wszystkich krawędzi. Wszystkie tafle miały tę samą grubość 8 mm. Dla wszystkich szyb przyjęto model materiału jako liniowo-sprężysty, o parametrach mechanicznych szkła E=70 GPa oraz ν = 0,23. Do tafli przykładano narastające obciążenie równomiernie rozłożone (co 100 N/m2, do 2000 N/m2). Dla uproszczenia pominięto ciężar własny szyb. Przeprowadzono dwa rodzaje analizy: liniową oraz nieliniową. Obliczenia wykonano metodą elementów skończonych (MES).
Wyniki obliczeń numerycznych przedstawiono na rys. 2. Przy typowych wymiarach szyby (o powierzchni do 1 m2), niezależnie od wartości przyłożonego obciążenia, wyniki obliczeń liniowych i nieliniowych są zbieżne. Przy większych wymiarach szyby (od 2 m2) różnice między wynikami obliczeń ugięć przy analizie liniowej i nieliniowej są wyraźnie różne. Dla szyby o długości boku równym 1500 mm różnica ta, dla obciążenia równego 2000 N/m2, wynosi 29,4%, a dla szyby o długości boku 2000 mm – 104,4%.
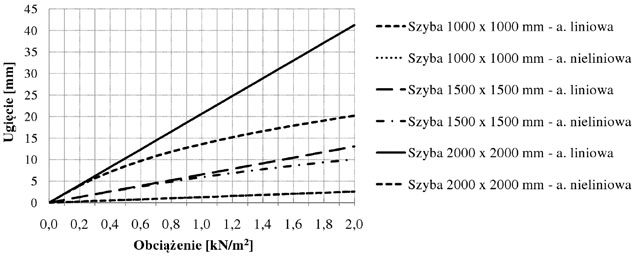
Rys. 2. Ugięcie w środku rozpiętości przy analizie liniowej i nieliniowej dla szyb kwadratowych o boku 1000, 1500 oraz 2000 mm i grubości 8 mm
Równolegle przeprowadzono obliczenia analityczne, używając inżynierskich metod liniowych. Odpowiednio, dla szyby o długości boku 1000, 1500, 2000 uzyskano ugięcia równe: 2,6 mm, 13,4 mm oraz 42,2 mm. Wyniki inżynierskich obliczeń potwierdzają z wystarczającą dokładnością (rozbieżność wyników 1,1%) wyniki analizy liniowej uzyskane z modelu numerycznego.
Kolejna analiza dotyczy przypadku wielkogabarytowej szklanej fasady. Analiza ugięć szklanych płyt została przeprowadzona na przykładzie elewacji Domu Handlowego „Wolf Bracka” w Warszawie, szczegółowo przedstawionej w pracy [1]. Szklana fasada na południowej ścianie budynku składa się z kilkunastu szyb zespolonych o wymiarach 2100x3830 mm i budowie 8/16/88.2 (8 mm szyba zewnętrzna wykonana ze szkła hartowanego, 16 mm przestrzeni wypełnionej gazem szlachetnym, szyba klejona 2x8 mm wykonana ze szkła hartowanego, bezpieczna – szyba wewnętrzna).
Analiza dotyczy zewnętrznej tafli szyby zespolonej o wymiarach 2100x3830 mm i grubości 8 mm. Analizę przeprowadzono w różnych wariantach zamocowania do elementów konstrukcji (rys. 3): dwa schematy podparcia liniowego wzdłuż wszystkich krawędzi (przegubowo-nieprzesuwny i przegubowo-przesuwny) oraz dwa schematy podparcia punktowego (wszystkie mocowania punktowe nieprzesuwne i standardowy sposób łożyskowania szyb mocowanych punktowo). Płyty zostały obciążone narastającym (co 100 N/m2, do 1000 N/m2) obciążeniem równomiernie rozłożonym, co miało odwzorowywać obciążenie wiatrem. Dla uproszczenia obciążenie ciężarem własnym szyby pominięto. Przeprowadzono dwa rodzaje analizy: liniową oraz nieliniową. Obliczenia wykonano metodą elementów skończonych (MES). Podobnie jak wcześniej, do obliczeń przyjęto model materiału szkła jako liniowo-sprężysty, o parametrach mechanicznych szkła E =7 0 GPa oraz ν = 0,23. Dodatkowo, dla liniowego schematu podparcia szyby dokonano weryfikacji wyników obliczeń numerycznych inżynierskimi metodami analitycznymi.
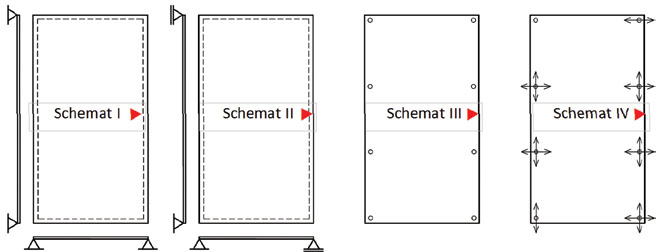
Rys. 3. Schematy statyczne szklanych płyt 2100x3830 mm (opis w tekście)
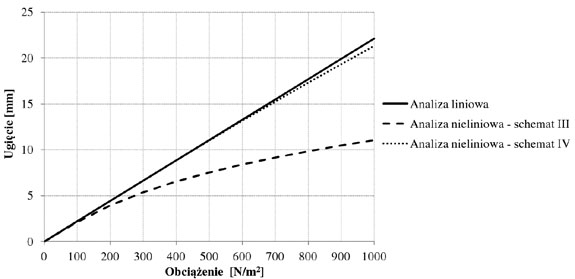
Wyniki obliczeń dla szyby podpartej liniowo przedstawiono w tabeli 1 oraz na rys. 4, a dla szyby podpartej punktowo w tabeli 2 oraz na rys. 5.
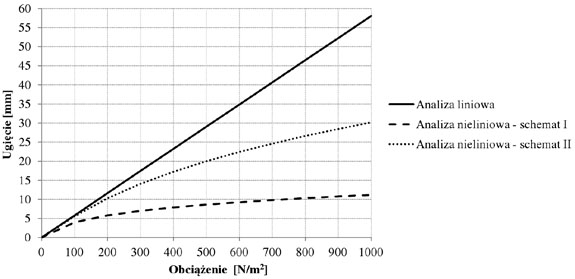
Rys. 4. Ugięcie w środku rozpiętości szyby podpartej liniowo o wymiarach 2100x3830 mm i o gr. 8 mm przy analizie liniowej i nieliniowej
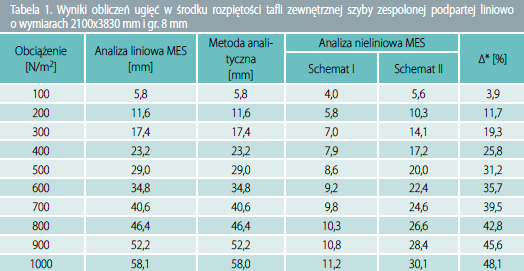
* różnica wartości ugięć dla analizy liniowej MES oraz analizy nieliniowej MES dla schematu II (przegubowo-przesuwnego)
Rys. 5. Ugięcie w środku rozpiętości przy analizie liniowej i nieliniowej dla szyby podpartej punktowo o wymiarach 2100x3830 mm i o gr. 8 mm
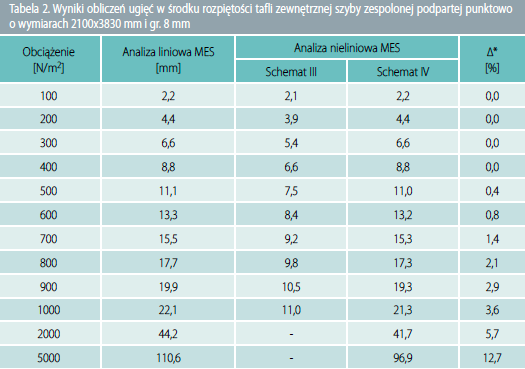
* różnica wartości ugięć dla analizy liniowej MES oraz analizy nieliniowej MES dla schematu IV
Wykres przedstawiony na rys. 4 pokazuje, że w przypadku szyb podpartych liniowo nie tylko rodzaj analizy, ale także sposób podparcia ma wyraźny wpływ na wyniki ugięć. Już przy niewielkich obciążeniach (200 N/m2) uzyskano wartości ugięć mniejsze o 50% (schemat I) i 11,7% (schemat II) dla analizy nieliniowej w porównaniu do analizy liniowej. Dla większych obciążeń różnice te są jeszcze większe. Dla obciążenia 1000 N/m2 wartości ugięć są mniejsze o 80,7% (schemat I) i 48,1% (schemat II). Równolegle przeprowadzono obliczenia analityczne, używając inżynierskich metod liniowych i uzyskano pełną zgodność z wynikami analizy liniowej z modelu numerycznego.
Wykres przedstawiony na rys. 5 wyraźnie pokazuje, że w przypadku szyb podpartych punktowo, w zakresie obciążeń do 1000 N/m2 sposób analizy nie ma większego wpływu na wyniki ugięć, za to istotny jest sposób podparcia modelu. W przypadku zamodelowania podparcia wszystkich punktów jako nieprzesuwnego uzyskano wyniki ugięć mniejsze o 50% (schemat III) dla analizy nieliniowej w porównaniu do analizy liniowej. W przypadku schematu podparcia IV wyniki ugięć dla analizy nieliniowej i liniowej są bardzo zbliżone (różnica 3,6%). Dopiero przy zdecydowanie większych obciążeniach (5000 N/m2) wyniki ugięć dla schematu podparcia II są mniejsze o 12,7%.
Podsumowanie
W przypadku wielkogabarytowych szklanych ścian osłonowych do poprawnego wyznaczania ugięć kluczowy jest dobór odpowiedniej metody obliczeniowej oraz schematu podparcia najbardziej zbliżonego do rzeczywistości. Przy niewielkich wymiarach szyb (do 1 m2) wyniki ugięć przy analizie liniowej i nieliniowej są zbieżne, stąd w takich przypadkach inżynierskie metody obliczania ugięć dają wystarczająco dokładne wyniki. Jednak tafle o takich wymiarach są stosowane bardzo rzadko. W przypadku szyb większych (powyżej 2 m2) wyniki ugięć przy analizie liniowej i nieliniowej oraz w zależności od przyjętego schematu podparcia, różnią się nawet kilkakrotnie. Wybór nieodpowiedniego rodzaju analizy oraz schematu statycznego do analizy wielkogabarytowych szklanych ścian osłonowych może zatem prowadzić do znacznych błędów i nieekonomicznego projektowania tych elementów.
Marcin Kozłowski
Literatura
[1] Kozłowski M.: Szkło jako materiał konstrukcyjny. Praca magisterska, Politechnika Śląska, Wydział Budownictwa, Gliwice 2009.
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 9/2014






































