Izolacyjna szyba zespolona (ISZ) działa jako złożony system, jego zachowanie strukturalne może być analizowane w zakresie liniowym, gdy rozpatrujemy tylko proste przypadki i może być obliczane analitycznie. Dlatego elementy szyby zespolonej (budowa, grubość szkła) są dziś określane przy zastosowaniu odpowiedniego oprogramowania komputerowego. Podstawy, na których oparte są te obliczenia, przedstawia poniższy artykuł.
Podstawy, szkło płaskie
Uniwersalną i fizycznie odpowiednią metodą projektowania szyb zespolonych jest metoda numeryczna wykorzystująca model Metody Elementów Skończonych1). Korzystając z tej metody możliwe jest projektowanie szyb zespolonych z wieloma taflami szkła (tafle płaskie lub zakrzywione), o dowolnej geometrii i budowie i z dowolnymi sposobami podparcia. Możliwe jest uwzględnienie działania różnych rodzajów obciążeń – również obciążeń punktowych – jak też uwzględnienie współpracy między elementami sklejonymi za pomocą folii (PVB, EVA, SGP). Jednak nie zawsze jest powinno się przyjmować liniowe zachowanie się poszczególnych tafli szklanych, gdyż może to przyczynić się do zaprojektowania szkła płaskiego ze znacznie mniejszymi grubościami.
1) Metoda Elementów Skończonych (MES, ang. FEM, finite-element method) – metoda rozwiązywania układów równań różniczkowych, opierająca się na podziale dziedziny (tzw. dyskretyzacja) na skończone elementy, dla których rozwiązanie jest przybliżane przez konkretne funkcje i przeprowadzaniu faktycznych obliczeń tylko dla węzłów tego podziału.
Dla wyjaśnienia zachowania oszklenia rozważany jest przypadek jednokomorowej szyby izolacyjnej, gdy w wyniku działania obciążenia zewnętrznego, np. parcia wiatru, wyginana jest zewnętrzna tafla szkła. Zmniejsza się więc objętość przestrzeni międzyszybowej, a ciśnienie wewnątrz szyby zespolonej wzrasta.
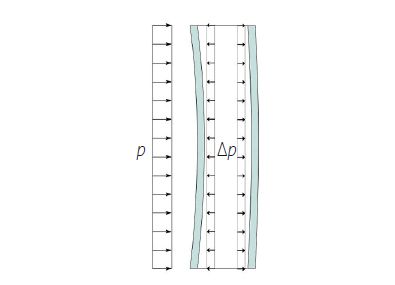
Rys. 1. Zachowanie się szyby jednokomorowej pod obciążeniem zewnętrznym p
Ten wzrost ciśnienia w komorze międzyszybowej utrzymywany jest jako obciążenie tafli zewnętrznej i tafli wewnętrznej. Podsumowując zatem, na zewnętrzną taflę działa obciążenie p-Δp, a na taflę wewnętrzną obciążenie Δp. Tak więc, łączne obciążenie jest podzielone na obie tafle.
Stopień tego rozkładu zależy od:
- sztywności tafli szklanych,
- objętości przestrzeni międzyszybowej wypełnionej powietrzem (lub gazem szlachetnym).
Obliczanie tego podziału obciążenia z uwzględnieniem ogólnego prawa gazu (patrz poniżej). Należy zauważyć, że w przypadku szkła laminowanego, że sztywność zależy nie tylko od geometrii, ale także przez połączenia między szybami.
Obciążenie klimatyczne (wpływ prężności gazu w przestrzeni międzyszybowej)
W zależności od miejsca zamocowania na oszklenie działają różne obciążenia zewnętrzne: od parcia wiatru, ciężaru śniegu, parcia tłumu oraz wynikające z różnic temperatury i ciśnienia między miejscem produkcji a miejscem montażu (instalacji) – co musi być rozpatrywane w trakcie projektowania szyb izolacyjnych.
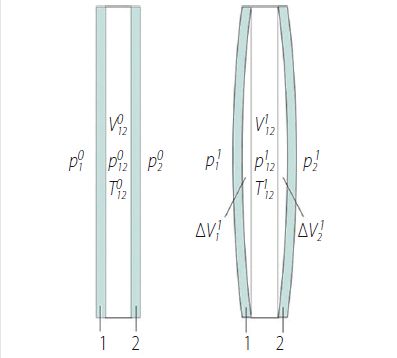
Rys. 2. Szyba jednokomorowa: po lewej opuszczająca miejsce produkcji (stan 0) i po prawej w miejscu montażu (stan 1)
Wewnątrz przestrzeni międzyszybowej znajduje się gaz wtłoczony w zakładzie produkcji szyb zespolonych
– charakteryzujący się ciśnieniem
i temperaturą
(stan 0).
Jeśli temperatura i / lub ciśnienia powietrza otaczającego w miejscu montażu (stan 1) są inne niż w miejscu produkcji, co powoduje że objętość gazu w zamkniętej komorze musi zmienić, co prowadzi do odkształceń tafli szklanych i powstawania naprężeń w szkle.
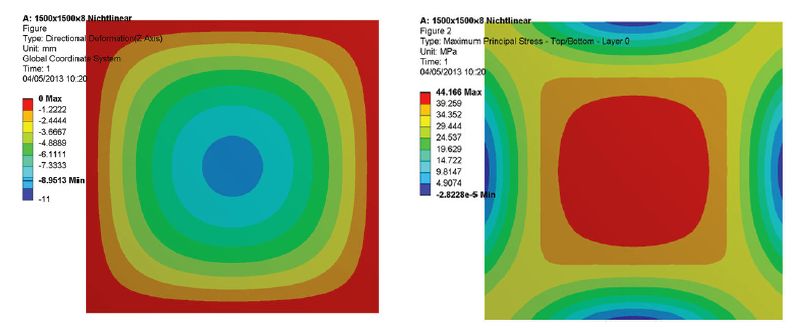
Rys. 3a+b. Naprężenia główne na tylnej płycie – z uwzględnieniem membrany - analiza nieliniowa
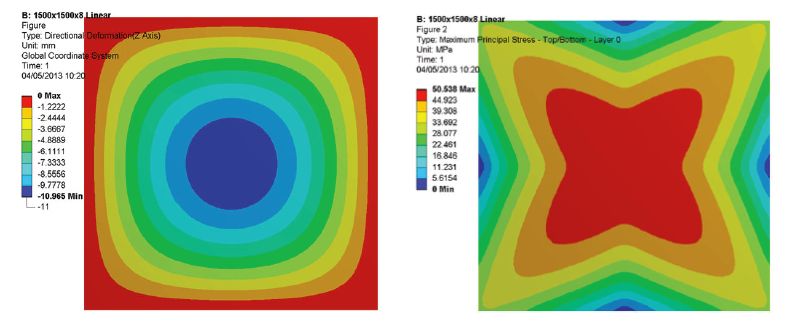
Rys. 3c+d. Naprężenia główne na tylnej płycie – bez uwzględnienia efektu membrany – analiza liniowa
Różnice temperatury do zastosowania w okresie letnim i zimowym są podane w przepisach [1] [2], jak również meteorologiczne różnice ciśnienia i różnice ciśnienia atmosferycznego zależne od różnicy wysokości między miejscem produkcji i montażu, z wartości tych można skorzystać jeżeli nie są dokładnie znane (zmierzone) wartości odnoszące się do konkretnego przeznaczenia danej partii szyb.
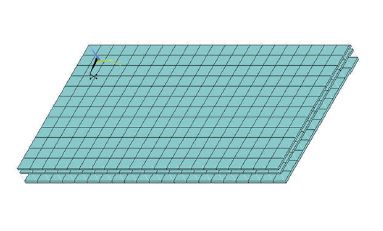
Rys. 4. Model MES dwukomorowej szyby izolacyjnej (z trzema taflami szkła) z elementami łączącymi do modelowania połączenia (uszczelnienia) krawędzi.
Dla obciążeń zewnętrznych, jak i obciążenia klimatycznego (zależnego od różnic prężności powietrza) odnosi się równanie ogólne gazu:
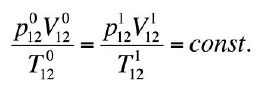
Objętość powietrza wewnątrz zamkniętej komory międzyszybowej V1 21 w stanie 1 wynosi więc V1 12 = V0 12 + ΔV11 + ΔV12.
Zmiany objętości ΔV11 i ΔV21 wynikają z odkształceń poszczególnych tafli szkła i są obliczane po scałkowaniu przemieszczeń punktów na powierzchni
tafli szklanych.
Tak więc:
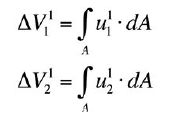
gdzie u11 i i u12 to ugięcia płyt 1 i 2 w stanie 1 (w odniesieniu do stanu 0). Wielkości ΔV11 i ΔV12 mogą być określone w analizie Metodą Elemetów Skończonych.
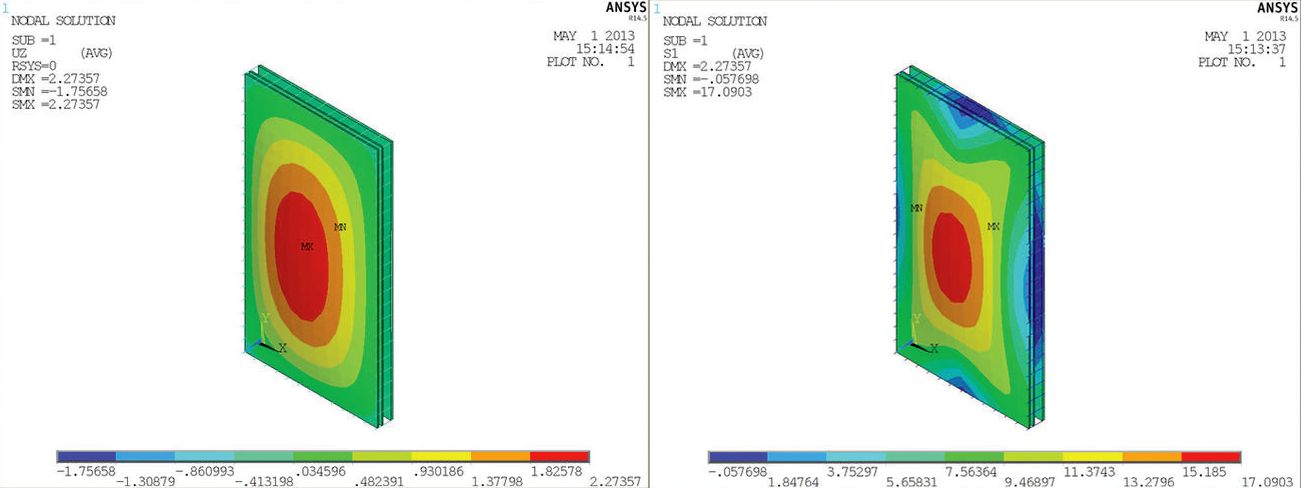
Rys. 5. Obciążenie klimatyczne w lecie dla szyby dwukomorowej o wymiarach 550 x 1000 mm i budowie 8-32-6-12-6: po lewej stronie wykres ugięcia, po prawej stronie naprężenia główne w szkle
Rozwiązanie liniowe
W pewnych warunkach, wartości ΔV11 i ΔV12 mogą być w dostatecznym przybliżeniu określone z następującego równania liniowego:
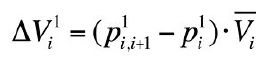
_
Vi stanowi zmianę objętości w wyniku odkształcenia tafli „i” pod wpływem jednostkowego obciążenia 1,0 kN/m2.
To równanie liniowe jest prawdziwe dla dowolnych kształtów, ale tylko dla szyb izolacyjnych podpartych ze wszystkich stron (na wszystkich krawędziach), i w tym przypadku każda tafla może być uznana, że pracuje niezależnie.
W przypadku jednokomorowej szyby izolacyjnej nieznane ciśnienie p1 12 (w szybie) może być obliczone z następującego równania kwadratowego:
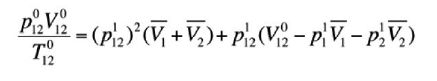
Analogicznie, dla dwukomorowej szyby izolacyjnej (z trzema taflami szkła) wartości ciśnień p1 12 i p1 23 (w poszczególnych komorach szyby) mogą być obliczone z układu dwóch równań kwadratowych.
Model numeryczny
Bardziej wszechstronne i bardziej dokładne obliczenia, możliwe do zastosowania w przypadku wszystkich typów podparcia i różnych rodzajów obciążeń obliczeniowych, mogą być realizowane za pomocą iteracyjnej2) metody obliczeń. Bezpośrednie rozwiązanie nie jest możliwe ze względu na nieliniowy charakter fizycznych równań gazu i ze względu na nieliniowy charakter geometrycznych odkształceń tafli szklanych, które mogą być brane pod uwagę w ramach opisanej poniżej metody Newtona-Raphsona3).
2) Iteracja (łac. iteratio – powtarzanie) – czynność powtarzania (najczęściej wielokrotnego) tej samej instrukcji (albo wielu instrukcji) w pętli.
3) Metoda Newtona-Raphsona (zwana również metodą stycznych) – iteracyjny algorytm wyznaczania przybliżonej wartości pierwiastka funkcji.
Często ugięcie tafli szklanej jest większe od grubości tej tafli i większe od 1/100 rozpiętości tafli szklanej. Deformacje w tym rozmiarze są szczególnie widoczne przy dużych rozmiarach płaskich tafli szkła, a efekt działania membrany zauważalny (zachowanie tafli szkła zbliżone do pracy wiotkiej membrany, a nie sztywnej płyty).
Przy rozpatrywaniu pracy tafli szkła przenoszącej obciążenia należy więc nie tylko rozpatrywać model zginanej płyty, ale również na zachowanie zbliżone do modelu membrany. Wzdłuż krawędzi tafli tworzy się pas z odkształceniem liniowym, a wewnątrz obszaru tafli charakter pracy jest zbliżony do membrany.
W konsekwencji przyjęcia takiego złożonego modelu otrzymuje się w wyniku obliczeń wielkości ugięć i naprężeń dużo mniejsze niż gdybyśmy przyjęli model czysto liniowy, nie biorąc pod uwagę efektu membrany.
Można to wykazać biorąc pod uwagę kwadratową taflę szklaną o rozmiarach LxB=1500x1500 mm i grubości t=8 mm, pracującą z obciążeniem powierzchni 5,0 kN/m2, zamocowaną liniowo na wszystkich krawędziach.
Do modelu wykorzystano tzw. lite elementy powłokowe. Szkło laminowane może być wykonane jako struktura: szkło-warstwa pośrednia-szkło. W zależności od tego, czy rozpatrujemy krótko- lub długotrwale działające obciążenie, warstwy pośrednie mogą być uważane za anizotropowe materiały z lub bez połączenia przekazującego naprężenia ścinające. Wpływ zarówno krótko- jak i długotrwałych obciążeń na strukturę systemową (np. obciążenie klimatyczne) może być uwzględniony i obliczony. Uzyskany stan odkształceń i naprężeń jest następnie „zamrożony”.
Właściwości materiału warstwy pośredniej mogą być modyfikowane, np. zmieniając się od pełnego do częściowego połączenia w kompozycie, i po przyłożeniu krótko- lub długotrwale działającego obciążenia (parcie wiatru, parcie tłumu) do odkształcającej się struktury.
W obliczeniach liniowych sklejenie krawędzi jest zastąpione zastosowaniem drobnych elementów, które łączą brzegi tafli szklanych. Siła generowana przez wyginanie się warstwy klejącej i odporność na ścinanie uszczelnienia krawędziowego szyby zespolonej są w założonym modelu pomijane.
Następnie posługując się modelem Newtona-Raphsona rozwiązujemy równania dla dwukomorowej szyby izolacyjnej (czyli z trzema taflami szkła), znajdując wartości dwóch nieznanych wartości ciśnień: p1 12 i p1 23
Ta metoda może być stosowana dla szyb wielokomorowych, z czterema lub więcej taflami szkła.
Ogólnie rzecz biorąc, dla funkcji F (x) dla x = x1, x2,…, xn ( ) wg równania Newtona-Raphsona: F(x +δx) = F(x)+ J δ x +O(δ x2 )
W naszym przypadku, wektor z nieznanymi wartościami ciśnienia, x = (x1, x2) = (p1 12, p1 23) i funkcji:
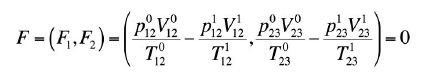
Drugiego i wyższego rzędu przyrosty O(δ x2) można pominąć.
Istotne jest określenie tzw macierzy Jacobiego4) J, która wskazuje kąt nachylenia wykresu funkcji F:

Gdy pochodne cząstkowe nie są określone, ciśnienie w komorze 1 zespolonej szyby izolacyjnej jest wykorzystywane do obliczania macierzy Jacobiego i początkowo może się nieco zmieniać, zmiana odpowiada x1=p12 zwykle 0,0001 kN/m2. Potem następuje zmiana wartości funkcji F1 i F2, obliczona na podstawie zmiany x1. To samo odnosi się do x2=p23 w drugim etapie.
Dla następnej iteracji wektora x doprowadza się następująco: xi+1=xi+δ x
Zmiana ciśnienia w izolacyjnej szybie zespolonej wynosi więc δx = F J1
Macierz Jacobiego powinna być więc odwracalna, co może czasami prowadzić do problemów numerycznych, które wymagają specjalnego traktowania.
Iteracja kończy się, gdy wszystkie wartości w wektorze δx są poniżej przyjętej dokładności obliczeń ε, - zwykle jest to 0,001 kN/m2.
4) Macierz Jacobiego – macierz zbudowana z pochodnych cząstkowych (pierwszego rzędu) funkcji, której składowymi są funkcje rzeczywiste. Nazwa pojęcia pochodzi od nazwiska niemieckiego matematyka Carla Gustawa Jacobiego, który je wprowadził.

Rys. 6: Model MES dla szyb zespolonych z płyt płaskich lub giętych (zakrzywionych).
Zwykle do osiągnięcia tej dokładności wyników jest wymagane tylko od 4 do 5 iteracji. Wykazano, że metoda jest zwykle zbieżna szybciej, jeśli nie będziemy wykonywać pełnego cyklu obliczeń określonego przez Newtona, ale dla wartości wektora zmiany ciśnienia, pomnożonej przez relaksacyjny współczynnik λ, którego wartość znajduje się pomiędzy 0,25 a 0,5 dla wygiętych szyb.
W początkowym etapie obliczania ciśnień należy po prostu użyć tzw. ciśnienia izochorycznego w płaskich szybach zespolonych. Postępowanie takie dla wygiętych szyb zespolonych nie jest wskazane, co opisane jest dalej.

Rys. 7: Model MES dla giętej szyby zespolonej jednokomorowej (złożonej z dwóch tafli szklanych).
Jak zaprojektować gięte szkło?
W adaptacji modelu numerycznego do szyb zespolonych złożonych ze szkła giętego należy najpierw rozróżnić dwa przypadki giętych szyb zespolonych:
złożone z płaskich i nieznacznie (lekko) wygiętych tafli oraz takich, które składają się z mocno wygiętych tafli szklanych.
Izolacyjne szyby zespolone – z płaskich lub lekko wygiętych tafli – projektuje się stosując procedury, jak dla szczególnego przypadku płaskich szyb zespolonych. Przykładowo, wygięte tafle szyby zewnętrzna i wewnętrzna zostały wytworzone jako część cylindrycznej powłoki ze zdefiniowaną przez użytkownika grubością. Do geometrycznego opisu szyby nadal można zastosować kartezjański układ współrzędnych5). Obliczenia są więc identyczne, jak w przypadku płyt płaskich.
Podejście różni się nieco w drugim przypadku, w którym wszystkie tafle w szybie zespolonej są mocno wygięte. Może tu wystąpić tak mocne wygięcie płyt, które powoduje, że niemożliwe jest korzystanie z kartezjańskiego układu współrzędnych. W takim przypadku określamy kształty geometryczne i obciążenia w cylindrycznym układzie współrzędnych6).
Inne kształty geometryczne, jak jednoosiowe krzywizny (tzw. powierzchnie prostokreślne7)), np. powierzchnie walcowe, mogą być analizowane w podobny sposób, ale konieczne jest dostosowanie parametrycznego modelu opracowanego przez autora.
Jakie są różnice między płaską a zakrzywioną – izolacyjną szybą zespoloną?
Konstrukcyjne zachowanie wygiętej płyty szklanej zasadniczo różni się pod wieloma względami od zachowania płaskiej tafli. Naprężenia w uszczelnieniu krawędzi w zakrzywionej izolacyjnej szybie zespolonej mogą być kilka razy większe niż w uszczelnieniu płaskiej szyby zespolonej. Naprężenie koncentruje się na krawędzi uszczelnienia, szczególnie na krawędzie wygiętej, nawet jeśli ta krawędź jest dłuższa w kierunku osiowym (rys. 4) (w przypadku płyt płaskich większe naprężenia są w uszczelnieniu na krótszej krawędzi szyby).
Podobnie siły przekazywane na miejsca mocowania są skumulowane na zakrzywionych krawędziach, co musi być wzięte pod uwagę przy projektowaniu takich konstrukcji. Największe naprężenia w szkle również skupiają się na obszarze wzdłuż zakrzywionych krawędzi i są tutaj wyraźnie większe niż – między innymi – w środku szyby lub na prostych krawędziach równoległych do osi cylindrycznej powierzchni szyby (tafle szyby giętej są najczęściej wycinkiem powierzchni walca).
5) Układ współrzędnych kartezjańskich (prostokątny) – prostoliniowy układ współrzędnych o parach prostopadłych osi. Nazwa pojęcia pochodzi od łacińskiego nazwiska francuskiego matematyka i filozofa Kartezjusza (wł. René Descartes), który wprowadził te idee w 1637 w traktacie La Géométrie
6) Walcowy układ współrzędnych (cylindryczny układ współrzędnych) to układ współrzędnych w trójwymiarowej przestrzeni euklidesowej. Każdy punkt P przestrzeni zapisuje się w postaci trójki współrzędnych (Φ, ρ, z), gdzie poszczególne składowe wyrażają się następująco:
ρ – odległość od osi OZ rzutu punktu P, na płaszczyznę OXY,
Φ – kąt pomiędzy osią dodatnią OX a odcinkiem łączącym rzut punktu P na płaszczyznę OXY z początkiem układu współrzędnych,
z – odległość rzutu punktu P na oś OZ od początku układu współrzędnych.
7) Powierzchnia prostokreślna – cała powierzchnia jest zbudowana z prostych, jak np.: powierzchnia stożkowa, walcowa, paraboloida hiperboliczna, hiperboloida jednopowłokowa, konoida, helikoida
Tafle szkła giętego – jak inne wygięte powłoki – mają znacznie większą sztywność w porównaniu do tafli płaskiej i przejmują duże obciążenie. Fakt ten ma taki skutek, że w porównaniu do identycznych płaskich tafli izolacyjnej szyby zespolonej wzrasta znaczenie obciążeń klimatycznych.
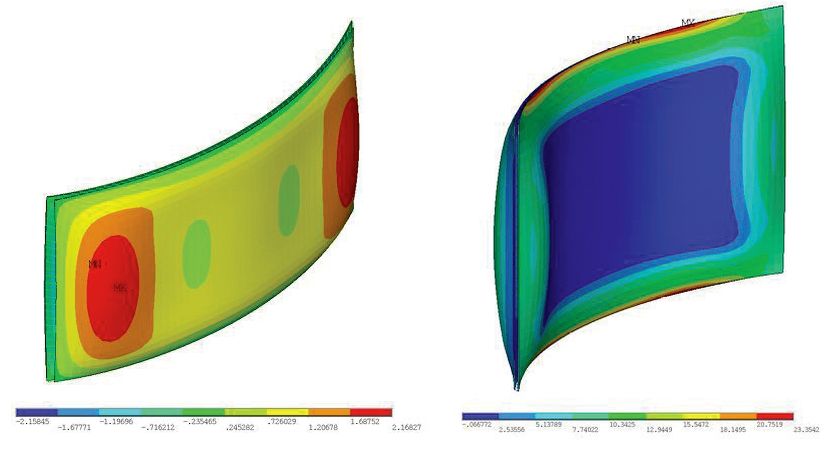
Rys. 8a: Odkształcenia zakrzywionej szyby zespolonej.
Rys. 8b: Naprężenia w zakrzywionej szybie zespolonej.
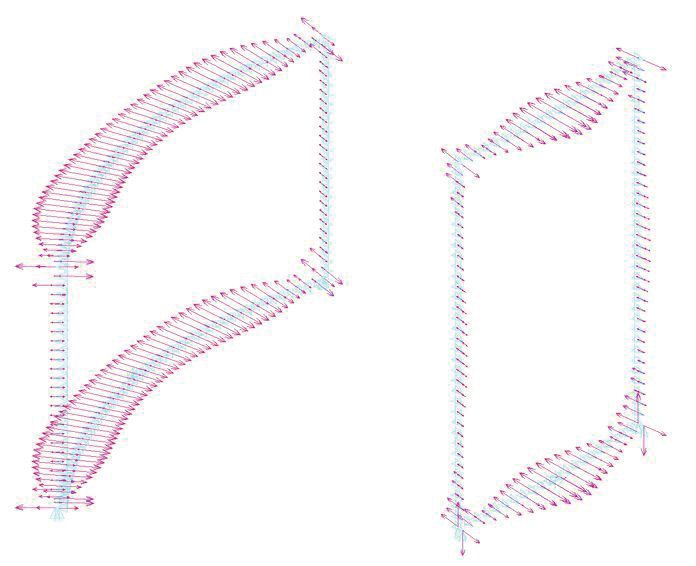
Rys. 9. Naprężenia w uszczelnieniu/spojeniu krawędzi szyby zespolonej dla różnych proporcji.
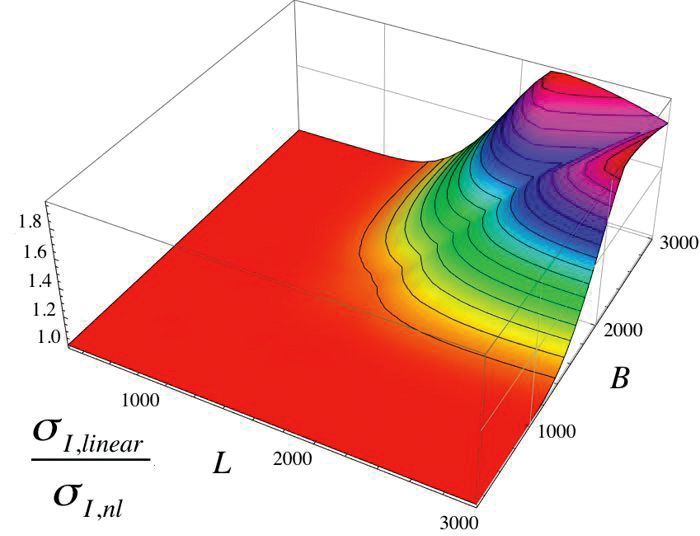
Rys. 10. Wpływ efektu membrany dla pojedynczej płaskiej płyty t = 12 mm, stosunek naprężeń głównych w modelach liniowym i nieliniowym, obciążenie powierzchniowe 4,0 kN/m².
Szyby gięte, zwłaszcza te z dużym promieniem krzywizny, są zagrożone utratą stabilności w warunkach podciśnienia. Zatem należy się przed tym w pełni zabezpieczyć. To z kolei stanowi niemały problem ze względu na strukturalną rolę szkła izolacyjnego.
Wielkość wpływu efektu membranowego zakrzywionych płyt zależy od kilku parametrów, np.: „intensywności” obciążenia, a w szczególności od współczynnika kształtu tafli, zależnego od stosunku długości sąsiednich krawędzi, oraz wielkości promienia krzywizny. Jak to konkretnie wygląda?
W przypadku płaskiej, pojedynczej tafli grubości t=12 mm i o wymiarach między 300x300 mm i 3000x3000 mm, jest to dość łatwe do określenia.
Ciekawe jest to, że największa różnica między naprężeniami z analizy liniowej i nieliniowej z efektem membrany występuje nie w przypadku kwadratowego kształtu tafli, ale dla prostokątnych arkuszy o proporcji boków około 4:3.
Teraz powstaje pytanie, czy wielkość efektu membrany może być powtórzona w przypadku szyby zespolonej? W szybie jednokomorowej występują dwa przeciwstawne efekty, w szczególności w przypadku obciążenia klimatycznego: z jednej strony, poszczególne tafle szklane, uwzględniając wpływ membrany, zachowują większą sztywność; z drugiej strony rośnie wpływ obciążenia klimatycznego, przy którym pozytywny wpływ efektu membrany z kolei się zmniejsza. Można to zobaczyć na załączonych wykresach, na których zamieszczono porównania wyników z analizy liniowej i nieliniowej.
Jako przykład izolacyjnej szyby zespolonej wybrano zestaw złożony z dwóch tafli 2x6 mm, a grubość komory między taflami wynosiła 16 mm. Obciążenie odpowiada obciążeniu klimatycznemu latem, czyli zgodnie z TRLV: ΔT=20°K, ΔΡmet = 2,0 kN/m2, ΔH = 600 m. Badania przeprowadzono dla różnych wymiarów tafli – w zakresie od 300x300 mm do 3000x3000 mm.
W obliczeniach nieliniowych okazało się, że występują większe naprężenia od obciążeń klimatycznych, maksymalna różnica w tym przypadku wynosi około 5%. Co ciekawe, największa różnica występuje głównie przy proporcjach długości krawędzi tafli 1:1, różnice są bardziej widoczne w przypadku większych tafli – przy wymiarach powyżej 1800 mm stają się już zauważalne. Wskazane są dalsze badania opisywanych analiz.
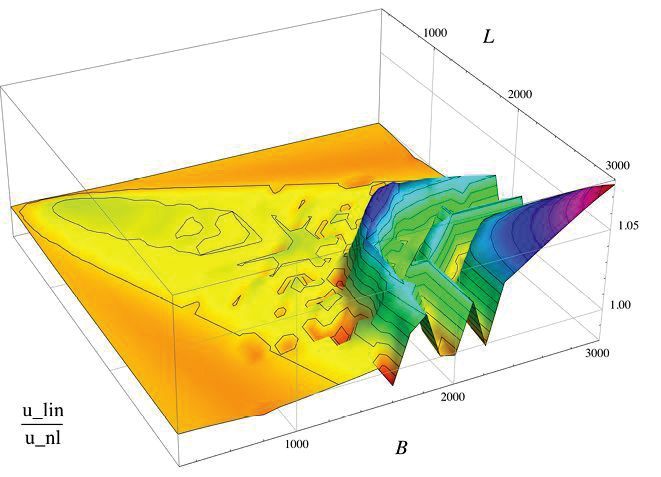
Rys. 11. Stosunek odkształceń w analizie liniowej i nieliniowej dla płaskiej izolacyjnej szyby zespolonej pod obciążeniem klimatycznym.
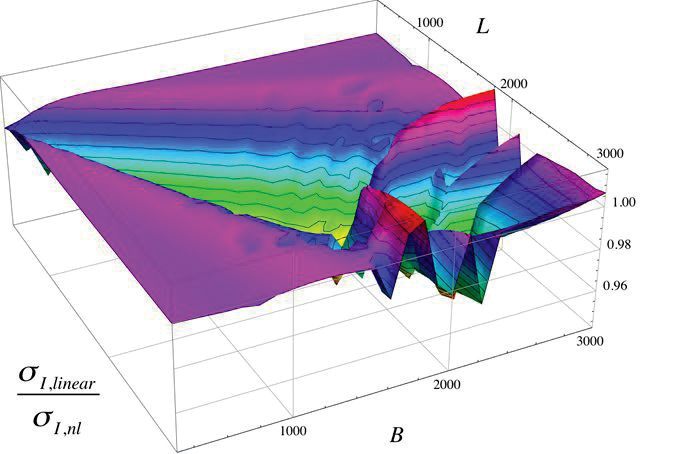
Rys. 12. Stosunek naprężeń głównych w analizie liniowej i nieliniowej dla płaskiej izolacyjnej szyby zespolonej pod obciążeniem klimatycznym.
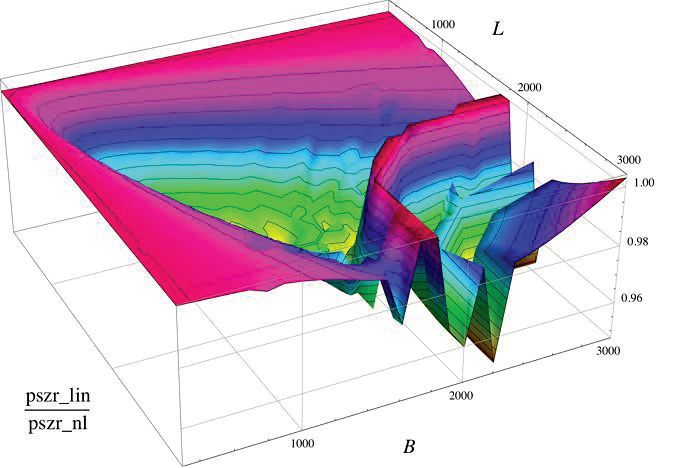
Rys. 13. Stosunek wartości ciśnień wewnątrz komory szyby dla płaskiej izolacyjnej szyby zespolonej pod obciążeniem klimatycznym.
Ze względu na duże obciążenia izolacyjnych szyb zespolonych, pozytywny wpływ efektu membrany na naprężenia i odkształcenia praktycznie jest neutralizowany – jeśli bierzemy pod uwagę obciążenia klimatyczne, poza wpływem parcia wiatru.
Nieco inaczej jest w przypadku zakrzywionego szkła izolacyjnego. W tym przypadku od określonej długości łuku występuje następujący efekt: powierzchnia ugięcia ma dwa obniżenia (minimalne wartości), i powraca do linii środkowej (rys. 3a). Wyjaśnieniem tego dziwnego na pierwszy rzut oka zjawiska wydają się proporcje wyników z analiz liniowych i nieliniowych. Kompozycja zestawu szyby zespolonej w tym przykładzie to 2x6 mm z komorą szerokości 16 mm, promień krzywizny zewnętrznej tafli szkła wynosi 3000 mm.
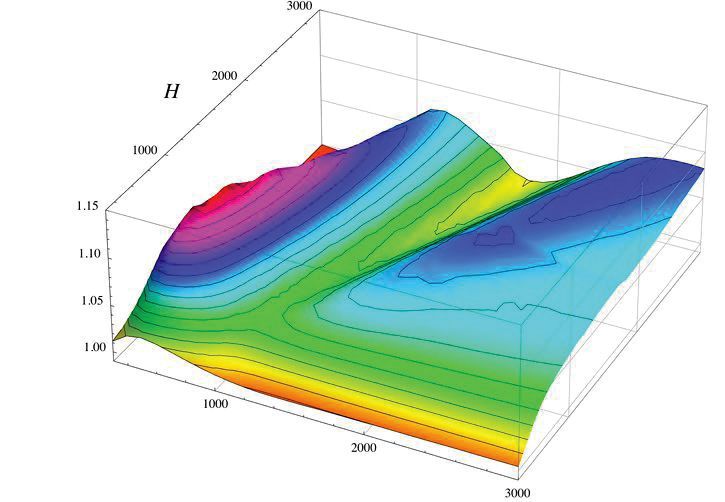
Rys. 14. Stosunek odkształceń w analizie liniowej i nieliniowej dla zakrzywionej izolacyjnej szyby zespolonej pod obciążeniem klimatycznym.
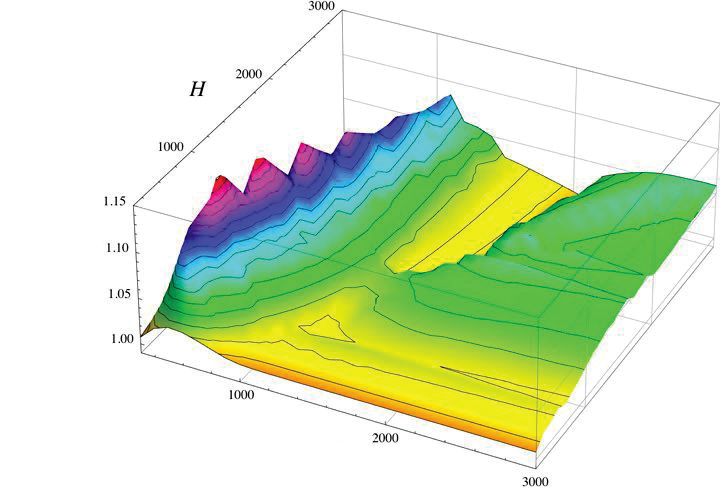
Rys. 15. Stosunek naprężeń głównych w analizie liniowej i nieliniowej dla zakrzywionej izolacyjnej szyby zespolonej pod obciążeniem klimatycznym.
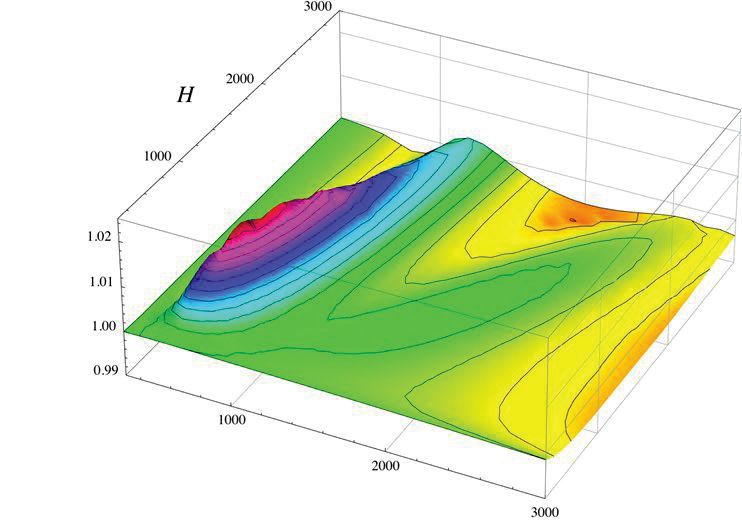
Rys. 16. Stosunek wartości ciśnień wewnątrz komory szyby dla zakrzywionej izolacyjnej szyby zespolonej pod obciążeniem klimatycznym.
Perspektywy
W podsumowaniu można stwierdzić, że nieliniowa analiza jest również opłacalna dla wygiętego szkła. W jakim jednak stopniu – to zależy od parametrów geometrycznych.
Nieliniowa analiza ma też tę zaletę, że fizycznie bardziej jest bliższa rzeczywistej pracy systemu szyby zespolonej. Ale także sprawia pewne problemy, na przykład na początku iteracyjnego stopniowego dochodzenia do prawidłowego wyniku, przyjęcie zbyt wysokiego ciśnienia w komorze izolacyjnej szyby zespolonej w stanie początkowym prowadzi do tego, że powstają niestabilne wyniki dotyczące naprężeń ściskających w taflach szklanych. W konsekwencji obliczenia nie są już konwergentne.
Czasami jednak problem rozdziału obciążeń na dwie tafle szklane nie jest tylko problem samych obliczeń numerycznych, ale przyjęciem w nich złych parametrów tafli szklanych (grubości, wytrzymałości).
Rozważania prowadzone w celu rozróżnienia tych dwóch przypadków mogą być w praktyce bardzo czasochłonne.
Eugen Schuler
„Glaswelt” 6, 7/2013
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacj: Świat Szkła 07-08/2013































