We współczesnym budownictwie, przy projektowaniu i wykonawstwie obiektów budowlanych jednym z materiałów zajmującym poczesne miejsce jest szkło, stosowane przede wszystkim w nowoczesnych rozwiązaniach obiektów uśyteczności publicznej, takich jak budynki biurowe, obiekty sportowe i handlowe, dworce itp.
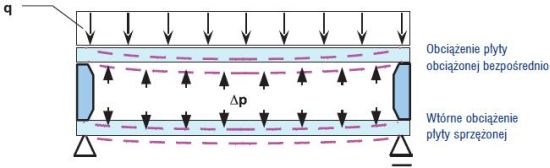
W elemencie złożonym z dwóch płyt szkła połączonych szczelną warstwą gazu (np. w szybie zespolonej) zachodzi sprzężenie gazowe obciążeń (rys. 1).
Współczynnik interakcji: Δp/q
Rys. 1. Interakcja międzyszybowa obciążenia powierzchniowego
Model matematyczny tego zjawiska przedstawiono w artykułach [1, 2, 3]. Sprzężenie gazowe liczbowo wyraża się zmianą ciśnienia gazu Δp w komorze międzyszybowej w odniesieniu do ciśnienia początkowego bez obciążenia układu.
Zmiana ciśnienia gazu jest związana ze zmianami objętości w komorze międzyszybowej, spowodowanymi objętością przemieszczenia płyt ograniczających komorę. Efektem sprzężenia gazowego jest interakcja, tzn. przekazywanie obciążeń między płytami zestawu.
Wypadkowe obciążenie płyty obciążonej bezpośrednio zmniejsza się kosztem wtórnego obciążenia płyty sprzężonej. Liczbowo interakcję pojedynczego obciążenia jednej z płyt można opisać współczynnikiem interakcji Δp/q, który wskazuje, jaka część obciążenia q przekazywana jest z szyby obciążonej bezpośrednio, na szybę gazowo sprzężoną.
W układzie, jak na rys. 1, zmiana ciśnienia wewnątrzkomorowego wynosi [2, 3,5]:
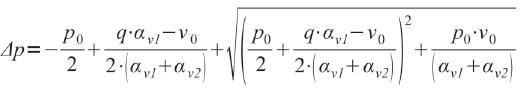(1)
gdzie: po, vo - początkowe ciśnienie gazu i objętość komory [kPa, m3],
αv - objętość przemieszczenia pojedynczej płyty zestawu pod obciążeniem 1 kN/m2 [m5/kN], indeks 1 dla płyty obciążonej, indeks 2 dla płyty sprzężonej,
q - wartość obciążenia, przy czym wartość dodatnia wskazuje na zwrot obciążenia do środka zestawu.
W przypadku swobodnego połączenia płyt z elementem dystansowym, współczynniki αv można oszacować ze wzoru:
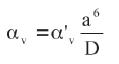(2)
gdzie:
a – szerokość (krótszy wymiar) płyty [m],
g – grubość płyty [m],
D – sztywność płytowa wyrażona wzorem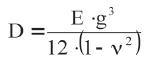
[kN·m]
gdzie:
E – moduł Younga [kPa]
ν – współczynnik Poissona,
α'v, – bezwymiarowy współczynnik według tab. 1.
Tabela 1. Współczynniki α'v, w zależności od stosunku długości do szerokości płyty s
Uwaga: s oznacza stosunek długości (dłuższego wymiaru) do szerokości płyty
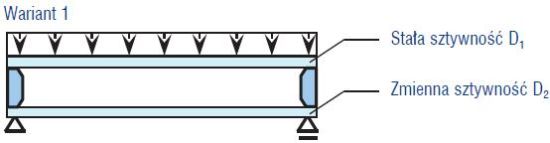
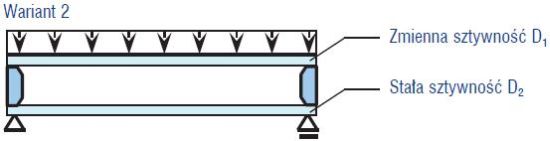
Rys. 2. Schemat założonych sztywności płyt zestawu
W niniejszym artykule analizowano wpływ zmian sztywności płyt zestawu na interakcję pojedynczego obciążenia. Rozpatrzono dwa warianty (rys. 2):
|
Wariant 1
Przebieg zmienności funkcji współczynnika interakcji, w zależności od sztywności płyty 2, zbadano dla przykładowych danych:
Wyniki analizy przedstawiono na rys. 3.
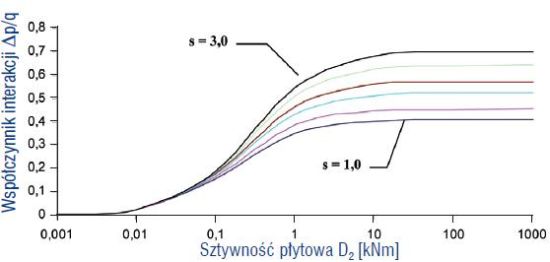
Rys. 3. Wpływ sztywności płyty sprzężonej na współczynnik interakcji pojedynczego obciążenia
Wariant 2
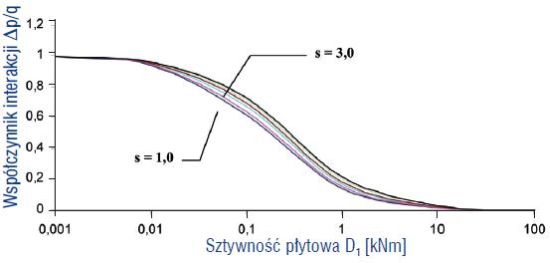
Przebieg zmienności funkcji współczynnika interakcji, w zależności od sztywności płyty 1 zbadano dla analogicznych danych, jak w wariancie 1.
Wyniki analizy przedstawiono na rys. 4.
Wnioski
W programach obciążeń płyt warstwowych ze szczelną komorą należy uwzględniać gazowe sprzężenia obciążeń, a następnie można obliczać siły wewnętrzne, naprężenie i przemieszczenie w obciążonych płytach, stosując metody klasycznej mechaniki konstrukcji.
Zależność współczynnika interakcji od sztywności płyt składowych zestawu ma tę własność, że im sztywniejsza jest płyta, tym większe obciążenie jest na nią przekazywane – jest to korzystne z punktu widzenia rozkładu naprężeń w elementach konstrukcji.
Zwiększenie wymiarów szyby skutkuje zwiększeniem współczynnika interakcji, co również jest korzystne, ponieważ maksymalne naprężenie w elemencie jest mniejsze, w porównaniu do układu płyt połączonych komorą nieszczelną, w którym interakcja nie występuje.
dr inż. Zbigniew Respondek
Literatura
Całość artykułu w wydaniu drukowanym i elektronicznym
patrz też: . Parametry techniczne nowoczesnych przegród szklanych. Część 1, Zbigniew Respondek, Świat Szkła 10/2007
oraz: - Przepływ energii promieniowania przez warstwowe zestawy szyb , Zbigniew Respondek, Świat Szkla 6/2005 - Modelowanie obciążeń klimatycznych szyb zespolonych. Część 2, Zbigniew Respondek, Świat Szkla 1/2005 - Modelowanie obciążeń klimatycznych szyb zespolonych. Część 1, Zbigniew Respondek, Świat Szkla 12/2004
więcej informacji: Świat Szkła 9/2010
inne artykuły o podobnej tematyce patrz Serwisy Tematyczne |
