Współczesne normy i kodeksy budowlane dotyczące praktyki projektowania wymagają oceny reakcji oszklonych powierzchni w odniesieniu do uderzeniowych oddziaływań dynamicznych, w celu uniknięcia kruchego pękania szkła.
Badanie odporności na uderzenia ciałem miękkim pozwala odtworzyć efekt przypadkowego uderzenia człowieka w przeszkloną konstrukcję, np. szklaną ściankę działową, całoszklaną balustradę lub przeszklone drzwi.
Jest to problem określenia wartości granicznych (nieokreślonej granicy styku), ponieważ odcisk masy uderzającej zmienia się wraz z wypadkową siły nacisku.
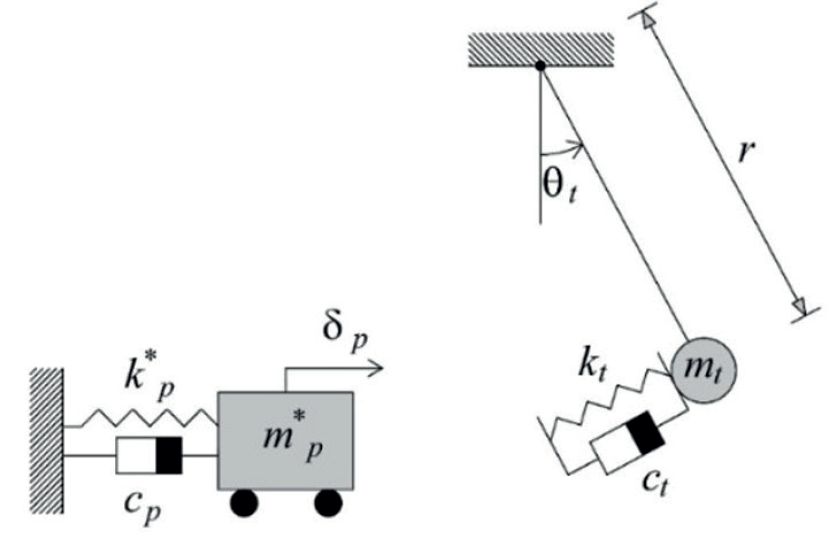
Rys. 1. Uproszczone systemy 2-DOF (z dwoma stopniami swobody), uzyskane z przybliżeniem à la Rayleigh dla panelu.
Po pierwsze, problemy dynamiczne analizuje się za pomocą uproszczonego podejścia opartego na równoważnym i nieliniowym systemie o dwóch stopniach swobody (2-DOF - two degree-of-freedom).
Maksymalne możliwe naprężenie w panelu, biorąc pod uwagę geometryczne nieliniowości, można uzyskać bezpośrednio z rozważań energetycznych, przyjmując rozsądne założenia. Sukcesywnie, w celu analizy złożonych problemów w rzeczywistych strukturach, opracowano inżynierskie narzędzie MES, które wykorzystuje nieliniowe jednostronne elementy belki i które można wdrożyć w większości komercyjnych programów do analizy strukturalnej.
Prognozy wyżej wymienionych metod są porównywane z badaniami eksperymentalnymi i wynikami uzyskanymi przy użyciu specjalnego oprogramowania do konstrukcji szklanych, przy ogólnie doskonałej zgodności. Badane są granice zastosowania uproszczonego podejścia. Opracowane narzędzie MES jest bardzo dokładne i stanowi ulepszenie w stosunku do dedykowanego oprogramowania, pozwalającego na uwzględnienie wielu uderzeń, tłumienia i dużej złożoności strukturalnej.
Wprowadzenie
Aktualne normy i kodeksy praktyki projektowej wymagają, aby wszelkie oszklenia stosowane w zastosowaniach architektonicznych były odporne na przypadkowe zdarzenia, w szczególności na oddziaływanie ludzi, bez uszkodzenia w stopniu nieproporcjonalnym do pierwotnej przyczyny, przy ograniczonym ryzyku obrażeń ludzi lub utraty mienia.
Norma EN 12600 [5] określa próbę uderzenia ciałem miękkim, o masie 50 (± 0,1) kg, złożonym z podwójnej opony pneumatycznej o nominalnym ciśnieniu wewnętrznym 3,5 (± 0,2) bar, zwisającym na linie w celu utworzenia wahadła. Wahadło upuszcza się z wysokości h i sprawdza się, czy szkło nie pęka lub jeśli pęka, czy fragmenty są nieszkodliwe (małej wielkości, z nieostrymi krawędziami – w przypadku szkła hartowanego lub czy kawałki szkła pozostają w całości przyklejone do folii laminującej – w przypadku szkła laminowanego).
Ta procedura jest w zasadzie eksperymentalna, ale istnieje uzasadniona potrzeba [9, 10, 13, 14] teoretycznego podejścia do przewidywania wyników badań.
W najczęściej stosowanym modelu, siła nacisku jest definiowana jako funkcja czasu: gdy jest znana, możliwe jest użycie standardowego oprogramowania MES do analizy równoważnego problemu statycznego. Zazwyczaj zakłada się, że odkształcenie ciała uderzającego jest uwzględnione w równaniu składowym dla sprężyny stykowej, toteż układ składa się z mas sztywnych połączonych przez (nieliniowe) zależności.
W przypadku oszklenia występuje trudność, ponieważ ciało uderzające jest miękkie, by odtworzać efekt uderzenia ludzkiego ciała i jest wykonane z komercyjnych opon pneumatycznych, których właściwości mechaniczne wykazują duże zróżnicowanie. Ponieważ ciało uderzające jest znacznie bardziej miękkie niż szkło, powierzchnia styku może się znacznie różnić podczas uderzenia, w przeciwieństwie do uderzenia sztywnymi ciałami lub pociskami [1].
Rzeczywiście, forma odcisku może znacznie wpłynąć na stan naprężeń w szkle: im mniejsza powierzchnia styku, tym większe jest naprężenie, które lokalnie dochodzi do nieskończoności w przypadku skoncentrowanych sił styku w teorii Kirchhoffa-Love’a dla liniowo elastycznych płyt. Dlatego należy rozwiązać problem nieokreślonej granicy styku, w którym należy określić rozmiar i formę obszaru styku.
Schneider i Schula [13] przeprowadzili serię testów ze znormalizowanym wahadłem uderzeniowym i zdefiniowali model, w którym sztywność opony jest schematycznie określona jako sprężyna liniowa. Aby rozważyć ewolucję odcisku, zakładając, że ciśnienie w oponie nie zmienia się podczas uderzenia, zdefiniowano model MES impaktora (ciała uderzajacego) jako zestawu elementów objętościowych zaimplementowanych do programu Ansys [2], który wytworzył homotetyczny (jednokładny), powiększający się wraz ze wzrostem siły nacisku odcisk o eliptycznym kształcie.
Podobne podejście jest stosowane w SJ Mepla [3], uznanym oprogramowaniu do obliczeń konstrukcji szklanych, ale dokumentacja objaśniająca nie podaje szczegółów. Co ważniejsze, SJ Mepla pozwala wziąć pod uwagę tylko jeden panel szklany, izolowany lub ułożony w ramie, biorąc pod uwagę odkształcalność tylnej konstrukcji nośnej poprzez ograniczenia sprężyste, co wyklucza rozproszenie.
Bardziej wyrafinowane oprogramowanie wielofunkcyjne, takie jak Abaqus lub Ansys, może obsługiwać kontakty unilateralne (jednostronne), choć za cenę znacznego wysiłku obliczeniowego, ale nie są one powszechnie dostępne w firmach projektowych, a w każdym razie procedura wprowadzania danych jest bardzo czasochłonna.
Tutaj, stosując metodę Rayleigha, zaczynamy od uproszczonej analizy, która redukuje problem do układu o dwóch stopniach swobody (2-DOF), z jednostronnymi sprężynami i elementami tłumiącymi wibracje. Pozwala to rozpoznać, że istnieją przypadki o znaczeniu praktycznym, w których bezwładność płyty ma drugorzędne znaczenie. Jeśli zostanie to pominięte, problem można rozwiązać za pomocą rozważań energetycznych, prawdopodobnie uwzględniając efekty nieliniowe.
Następnie opracowujemy kontaktowy model MES, zaimplementowany w większości komercyjnych programów do analizy strukturalnej, przy użyciu nieliniowych elementów belkowych. Porównania z wynikami eksperymentów [9] i wynikami uzyskanymi za pomocą SJ Mepla, przynajmniej w prostych przypadkach, które to oprogramowanie może obsłużyć, potwierdzają doskonałą dokładność proponowanego narzędzia MES.
Analizy ograniczają się do monolitycznych szklanych płyt, ale stosując koncepcję efektywnej grubości [8, 15], metodę można łatwo rozszerzyć na szkło laminowane.
Model 2-DOF (z dwoma stopniami swobody)
Problem dynamiczny jest najpierw analizowany jako układ z dwoma stopniami swobody, utworzony przez oscylator harmoniczny (panel szklany) i proste wahadło (wahadło z dwoma oponami) w jednostronnym kontakcie.
Model różni się od modelu [13], w którym wahadło jest również schematycznie odwzorowane jako oscylator harmoniczny, nie wprowadza się rozproszenia, a możliwość wielokrotnych uderzeń nie jest brana pod uwagę.
Poniżej wszystkie wartości (oznaczenia), odnoszące się do szklanego panelu lub wahadła z oponami, zostaną oznaczone odpowiednio przyrostkiem „p” lub „t”.
Zakładając liniową odpowiedź sprężystą, płytę szklaną redukuje się do oscylatora harmonicznego metodą Rayleigha [4].
W paradygmatycznym przykładzie prostokątnego szklanego panelu α × b swobodnie podpartego z czterech stron, przesunięcie zewnętrzne w (x, y, t) określa się poprzez funkcję kształtu w formie równań:
![]()
gdzie δp(t) to przemieszczenie w środku panelu.
W innych warunkach brzegowych można odpowiednio zdefiniować Ψ (x, y). Normowa procedura [4] pokazuje, że jeżeli pp jest masą panelu na jednostkę objętości, th to grubość, D = Eth3 / [12 (1-ν2)] sztywność na zginanie (E=7000 MPa i ν=0,22, a moduł Younga ze współczynnikiem Poissona dla szkła), efektywna masa mp* i sztywność kp* odczytane są odpowiednio ze wzorów poniżej.
![]()
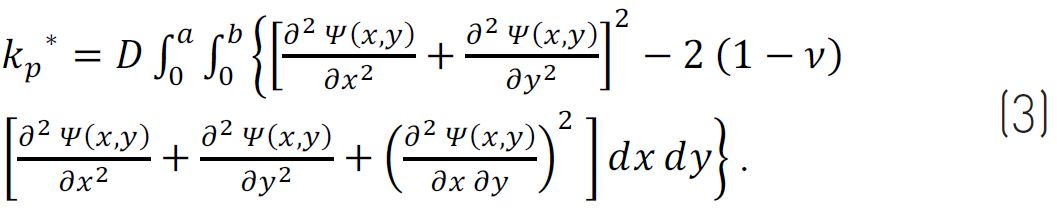
Jak pokazano na rys. 1, impaktor jest schematycznie przedstawiany jako zwykłe wahadło o masie mt = 50 kg [6], z liną (zawieszeniem) o długości r. Odkształcalność opony podczas uderzenia jest odwzorowane jako równoważna sztywność kt = 400 kN/m, zgodnie z pracą Schneidera i Schula [13].
Oznaczając za pomocą Θt(t) kąt, który lina naprężona tworzy z pionem, pierwsze uderzenie występuje w czasie t = 0 przy Θt(t) = 0. Po pierwszym uderzeniu przemieszczenie środka płytki δp(t), a także przemieszczenie opony δt(t), są małe w stosunku do r, tj. Θt(t)«1 i δt(t) = r Θt(t ).
Jeśli h jest wysokością zrzutu (opadania wahadła), a g jest przyspieszeniem grawitacyjnym, z bilansu energetycznego otrzymuje się Θt(0) = √ 2gh/r.
Można dodać tłumiki lepkościowe, z tłumieniem dla opon ct ustawionym na 5÷10% tłumienia krytycznego oscylatora wahadłowego cct=2Mt√g/r, a dla panelu cp = 0,1-0,5%ccp, z ccp= 2√Mp*Kp*.
System jest sprzężony, gdy δt(t)-δp(t)≥0. tzn. opona pozostaje przymocowana do szklanej płyty, nie sprzężony (odłączony), gdy δt(t)-δp(t)<0. Parametry ruchu można znaleźć, rozwiązując odpowiednio odpowiednie układy równań.
Wyniki tego podejścia są teraz porównywane z wynikami badań eksperymentalnych [10], dla panelu (axb = 876 x 1938 mm, th = 10 mm) uderzonego w jego środek (r=b/2, wysokość zrzutu h=450 mm.
Rys. 2a porównuje, w funkcji czasu t, przyspieszenie opony w modelu tłumionym (cp = 0,005 ccp i ct = 0,05 cct) δtd(t) i modelu nie tłumionym δtnd(t) z wynikami eksperymentalnymi δte(t).
Odpowiednie wartości przyspieszenia panelu w punkcie centralnym, tj. δp.d(t), δp.nd(t) i δp.e(t) pokazano na ryc. 2b. Kształty wykresu ściśle podążają za danymi eksperymentalnymi, będąc typami osiągniętymi w badaniach eksperymentalnych.
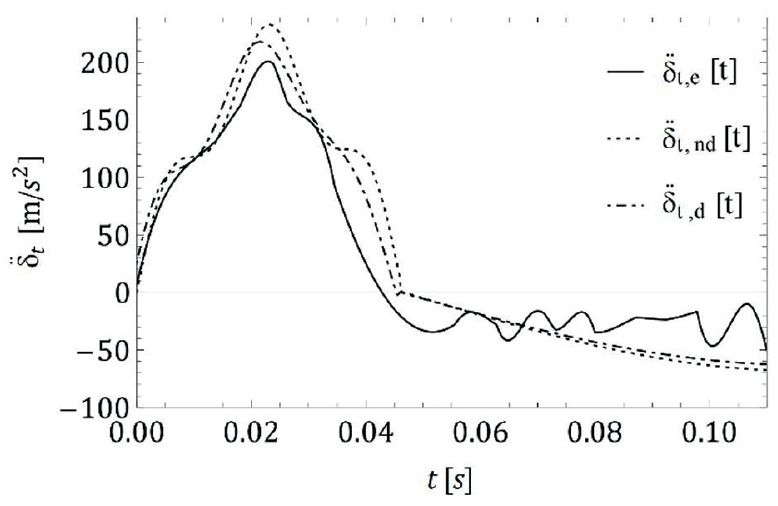
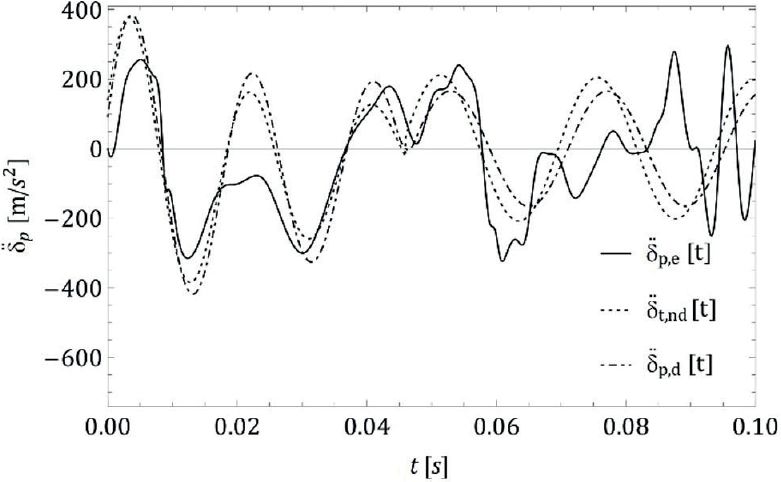
Rys. 2. Szyba 1938x876x10 mm, wysokość zrzutu h = 450 mm.
a) przyspieszenie opony z eksperymentów δt.e(t) oraz odpowiednio modele z tłumieniem i bez tłumienia oraz δt.d(t), бt.nd(t).
b) przyspieszenie w centrum panelu z eksperymentów δp.e(t) i modele z tłumieniem δp.d(t) i bez tłumienia δp.nd(t).
Rys. 3 przedstawia porównanie odkształceń εx.e(t) i εy.e(t), eksperymentalnie zmierzonych [10] na środku panelu, z odpowiednimi wartościami εx.nd(t) i εy.nd(t) uzyskane z modelu bez tłumienia (rys. 3a) oraz εx.d(t) i εy.d(t) pochodzące z modelu z tłumieniem (rys. 3b).
Należy zauważyć, że szczyt (punkt maksymalny) krzywych jest osiągany w przybliżeniu w tym samym czasie, a kształt jest porównywalny, szczególnie w przypadku odkształcenia w kierunku y.
Ta analiza pokazuje, że model z tłumieniem jest dokładniejszy niż model bez tłumiena, co podkreśla znaczenie tłumienia dla opony wykonanej z gumy.
Ponieważ jednak analiza liniowa pomija efekty drugiego rzędu w ugięciu panelu, błędy mogą być wyższe niż 10%.
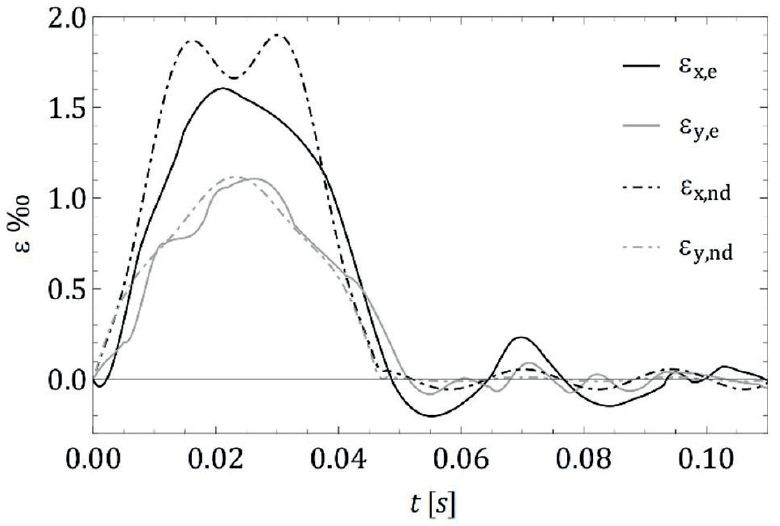
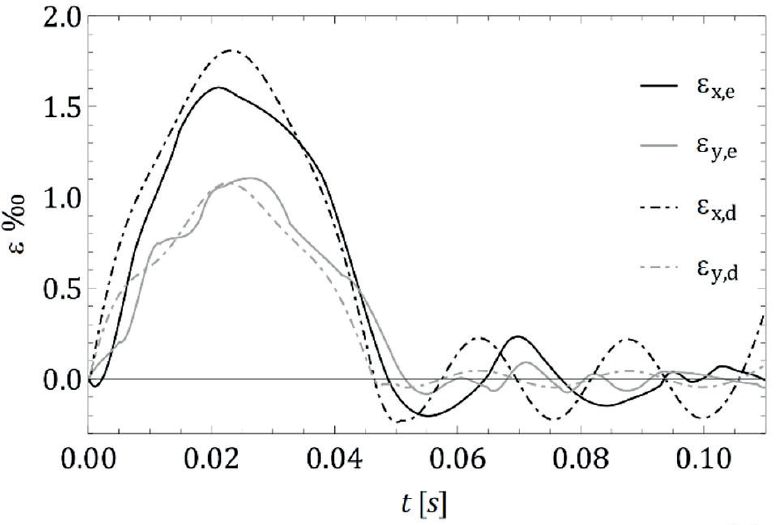
Rys. 3. Szklany panel 1938x87x10 mm, wysokość zrzutu = 450 mm. Porównanie eksperymentalnie zmierzonych odkształceń w środku εx.e i εy.e, które uzyskano z:
a) modelu bez tłumienia (εx.nd i εy.nd),
b) modelu z tłumieniem (εx.d i εy.d).
Podejście energetyczne i analiza nieliniowa
Naprężenie i odkształcenie szkła wynika z nacisków przenoszonych przez odcisk opony i działanie sił bezwładności związanych z przyspieszeniem panelu.
Odpowiednie odkształcenia, odpowiednio nazwane (εx,f, εy,f ) i (εx,m, εy,m), są wykreślone na rys. 4 dla modelu z tłumieniem, wraz z ich sumą (εx, εy). Należy tutaj zauważyć, że wpływ bezwładności jest mniejszy niż 5% całości.
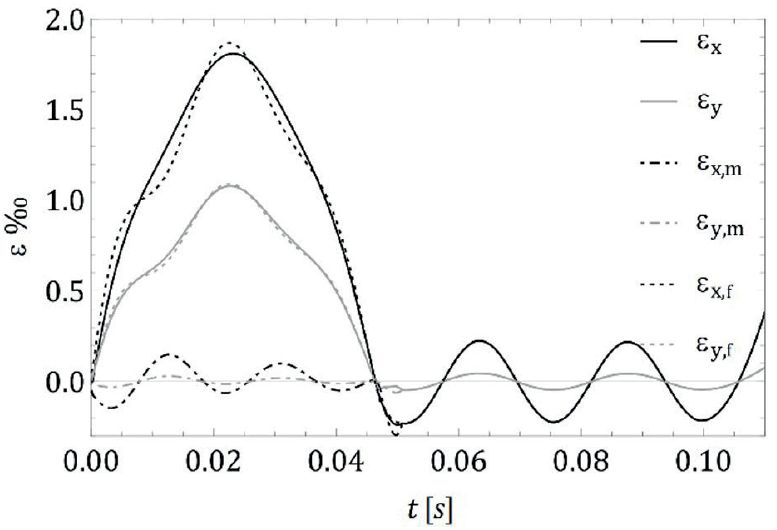
Rys. 4. Rozkład odkształceń εx i εy, w części spowodowanych bezwładnością, εx,m i εy,m oraz tych spowodowanych odciskiem opony, εx,f i εy,f
Nie jest to zaskakujące, ponieważ w wyrażeniu efektywnej masy mp* z [2] tylko niewielka część masy panelu uczestniczy w ruchu, ponieważ funkcja kształtu jest prawie zerowa w odniesieniu do zamocowanych krawędzi.
Analizę układu dynamicznego 2-DOF z rys. 1 można znacznie uprościć w granicy mp* → 0, pozwalając uwzględnić nieliniową sprężynę kp w celu uwzględnienia efektów zginania drugiego rzędu w płycie.
Wartość kp można obliczyć bezpośrednio za pomocą standardowej analizy (geometrycznej) nieliniowej MES, obserwując, że dla wspólnego rozmiaru płyt i ciśnienia opony jest ona w praktyce niezależna od obszaru odcisku opony A(t).
Zilustrowano to na rys. 5, na którym przedstawiono przesunięcie środka panelu w funkcji przyłożonej siły F, skoncentrowanej lub rozłożonej na powierzchni kwadratowej (140,1 mm2), w trybie liniowym lub nieliniowym: wykresy są prawie niezależne od sposobu, w jaki obciążenie jest przenoszone (skoncentrowane lub rozłożone).
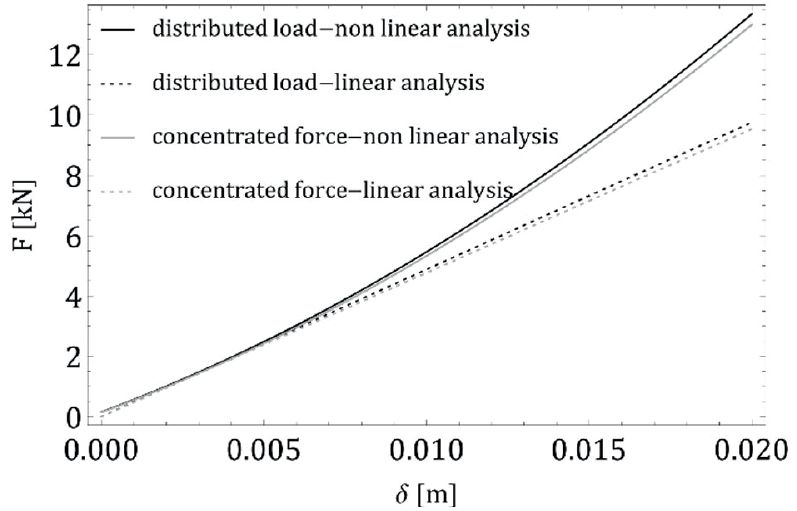
Rys. 5. Swobodnie podparty panel szklany 876x1938x10 mm z obciążeniem skoncentrowaną siłą lub z obciążeniem rozłożonym na kwadratowym obszarze. Analiza liniowa i (geometryczna) nieliniowa (obliczenia z wykorzystaniem MES za pomocą Straus7)
Wyniki są bardzo różne pod względem naprężenia, ale aby ocenić dynamiczną interakcję między panelem a impaktorem, ważna jest tylko sztywność panelu.
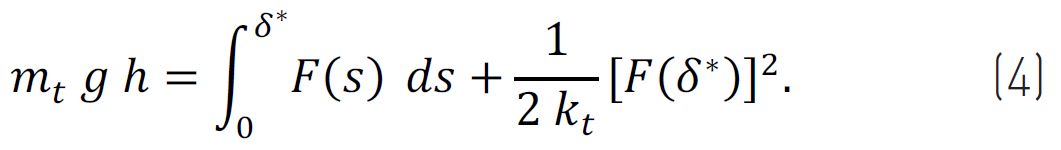
Co ciekawe, maksymalną siłę przenoszoną na panel można łatwo obliczyć z bilansu energetycznego z hipotezy, że maksymalna energia odkształcenia zarówno w kp, jak i kt jest osiągana, gdy energia kinetyczna jest zerowa, warunek zweryfikowany w granicy mp* → 0.
Jeśli F (δ *) to siła w funkcji przemieszczenia - prawo dla (nieliniowej) sprężyny kp, ponieważ w równowadze siła przenoszona przez kp jest taka sama jak siła wywierana przez kt, oznaczając δ* maksymalne przemieszczenie kp, równowaga energetyczna pozwala znaleźć δ*, a zatem siła nacisku F (δ*) ze wzoru
Tutaj sprężyna kt ma być liniowa, ale dla tego przypadku można również wziąć pod uwagę efekty nieliniowe. Aby określić stan naprężenia (бx, бy) w panelu, można obliczyć obszar odcisku A(δ*) = F(δ*)/p przy p = 3,5 bar, a następnie zastosować standardową analizę MES .
Dla rozpatrywanego panelu, przy użyciu krzywej siły w funkcji przemieszczenia z rys. 5, wyniki podsumowane w tabeli 1 są porównywane z wynikami uzyskanymi z nieliniowej analizy dynamicznej za pomocą SJ Mepla. Maksymalny błąd względny jest rzędu 6%. W liniowym sprężystym przypadku (sprężyny liniowe) maksymalny błąd jest rzędu 8%.
Tabela 1. Maksymalne naprężenia бx, бy i maksymalne przemieszczenie panelu δp, dla panelu 876x1938x10 mm, wysokość zrzutu h = 450 mm, mt-50. Wyniki z nieliniowego bilansu energetycznego i dynamicznej nieliniowej analizy programu SJ Mepla

Model kontaktowy MES i jego praktyczne zastosowanie
Warunki podparcia, które może rozważyć SJ Mepla, są w jakiś sposób ograniczone. Aby przeanalizować złożone problemy w rzeczywistych konstrukcjach, zgodnie z wymogami norm [5], proponujemy model kontaktowy możliwy do wdrożenia w zasadach komercyjnych do analizy strukturalnej, ponieważ modyfikacja obszaru kontaktu w przypadku uderzenia jest osiągana przy użyciu standardowych nieliniowych elementów belkowych .
Opona jest modelowana jako masa punktowa mt = 50 kg, przymocowana do wahadła o długości r z wysokością zrzutu h, uderzając w szybę w czasie t = 0 z prędkością √2gh. Działanie przywracające wahadła, jeśli oscylacje są małe, można odtworzyć za pomocą sprężyny o sztywności k = mtg/r, aby w razie potrzeby modelować wiele uderzeń.
Masa jest połączona z płytą poprzez „skrzynkę stykową”, której funkcją jest przenoszenie nacisku stykowego p na panel szklany w eliptycznym kształcie, przy czym zwiększa się homotetycznie wraz ze wzrostem wypadkowej siły nacisku. Jak na schemacie z rys. 6a, masa mt jest połączona ze skrzynką stykową przez sprężynę kt = 400 kN/m [13], symulując sztywność wewnętrzną opony.
Szklany panel ma siatkę z prostokątnymi elementami płytowymi. Jak pokazano na rys. 6b, każdy węzeł obszaru styku jest połączony, w obrębie skrzynki stykowej, z odpowiednim (zwierciadlanym) punktem na sztywnej płycie bez masy za pomocą dwóch belek połączonych szeregowo, jednej zwanej belką szczelinową, a drugiej belką łączącą. Ta ostatnia jest przymocowana jednym końcem do węzła na płycie, podczas gdy drugi koniec jest połączony z belką szczelinową, która z kolei jest połączona z odpowiednim punktem na sztywnej płycie.
Obie belki mają w sumie wysokość 2 mm, która jest znacznie większa niż maksymalna różnica przesunięć w obszarze styku z powodu ugięcia szklanej płyty. Belka szczelinowa zapewnia jednostronny kontakt, ponieważ jej sztywność osiowa jest zerowa (element nieaktywny), jeżeli względne przemieszczenie jej końców (wydłużenie) nie jest mniejsze niż δ szczelina (gdzie δgap jest szczeliną).
W przeciwnym razie staje się nieskończona (element aktywny). Szczelina δgap zmienia się w zależności od paraboloidalnej powierzchni pokazanej na rys. 6b, tak że gdy sztywna płaszczyzna jest dociskana do szklanego panelu, aktywne belki szczelinowe leżą w eliptycznym obszarze, czego dowodem jest czerwony kolor na ryc. 6c.
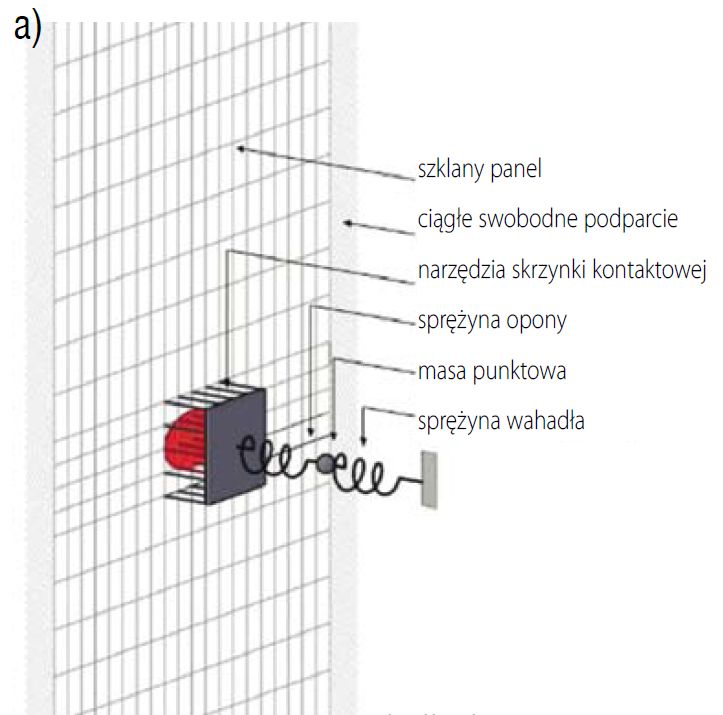
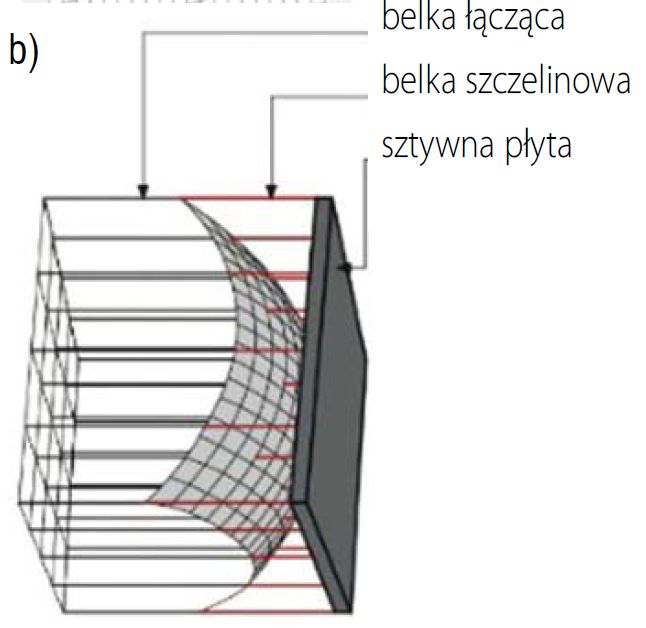
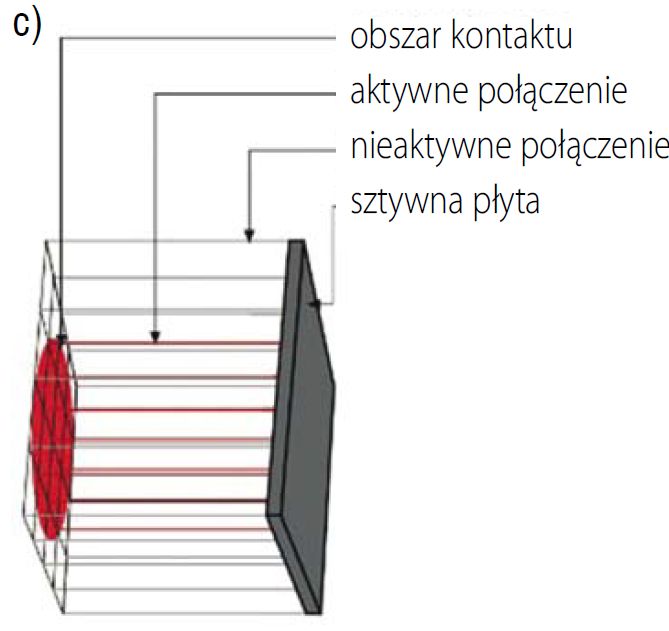
Rys. 6. Schemat skrzynki stykowej
a) Montaż skrzynki stykowej z siatką na płycie, masa opony mt oddziałuje przez sprężynę kt,
b) profil paraboloidalny dla δgap,
c) wynikowy eliptyczny kontaktowy obszar odcisku z aktywnych elementów
Oczywiście, każda belka łącząca staje się aktywna tylko wtedy, gdy aktywna jest belka szczelinowa, z którą jest połączona. Belka łącząca jest sztywno-plastyczna, tzn. przenosi stałą siłę osiową, która jest ustawiona na wartość ρAi, gdzie ρ = 3,5 bara, a Ai jest jego obszarem oddziaływania na płytę.
Podsumowując, układ złożony ze szczeliny i belki łączącej ustawionych szeregowo działa tylko przy ściskaniu, gdy opona wypycha płytę poza szczelinę δgap; w przeciwnym razie nie oferuje jakiekolwiek ograniczenia (jeśli wszystkie elementy są nieaktywne, mt odłącza się od płyty).
Tłumiki lepkościowe można również wstawiać równolegle ze sprężynami, ale nie robi się tego tutaj. Wszystkie użyte elementy belki są dostępne w bibliotece Straus7. To narzędzie pola kontaktowego stanowi postęp w stosunku do SJ Mepla, ponieważ pozwala uwzględnić całą strukturę.
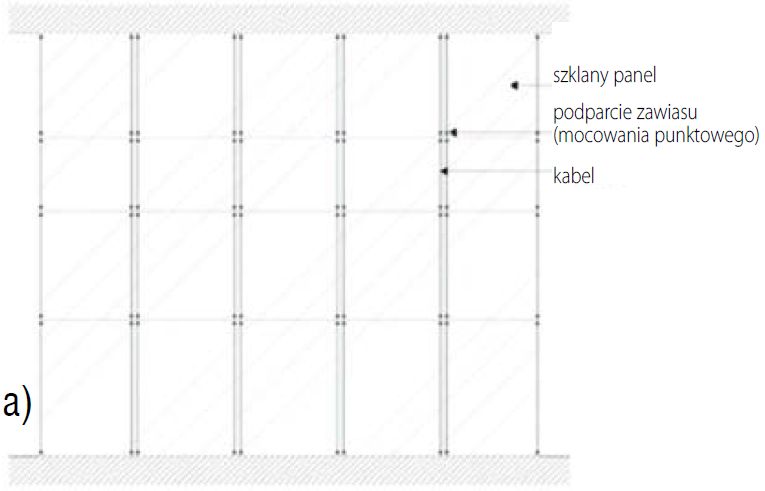
Rozważając studium przypadku [11] fasady opartej na pojedynczych kablach, przedstawionej na rys. 7a (kable długości L= 7,48 m o powierzchni przekroju A = 7,48 cm2, wstępnie napięte siłą N = 15,9 kN). Fasada składa się z 20 szyb, dzielących powierzchnię na kolumny o szerokości 1,75 m, 1,79 m, 1,79 m, 1,79 m i 1,75 m oraz rzędy o wysokości 2,38 m, 1,9 m, 1,3 m, 1,9 m (od dołu do góry).
Każda kolumna ze szklanymi panelami jest wsparta dwoma kablami w pobliżu krawędzi, za pomocą specjalnych urządzeń do mocowania punktowego paneli szklanych [7-12], zapewniając podparcie statycznie równoważne zawiasom na czterech wierzchołkach (punktowe mocowania oznaczone kropkami na rys. 7a), z dwoma punktowymi mocowaniami u górnych wierzchołków umożliwiającymi przesuwanie się kabla w celu umożliwienia ruchów termicznych.
Ponieważ w chwili badań dostępna podłoga była położona w przybliżeniu na połowie wysokości elewacji, weźmie się pod uwagę uderzenie miękkiego ciała w środkowy panel, z wysokością zrzutu wynoszącą h = 0,9 m. Każdy panel jest wykonany ze szkła monolitycznego 16 mm, modelowanego za pomocą elementów płytowych.
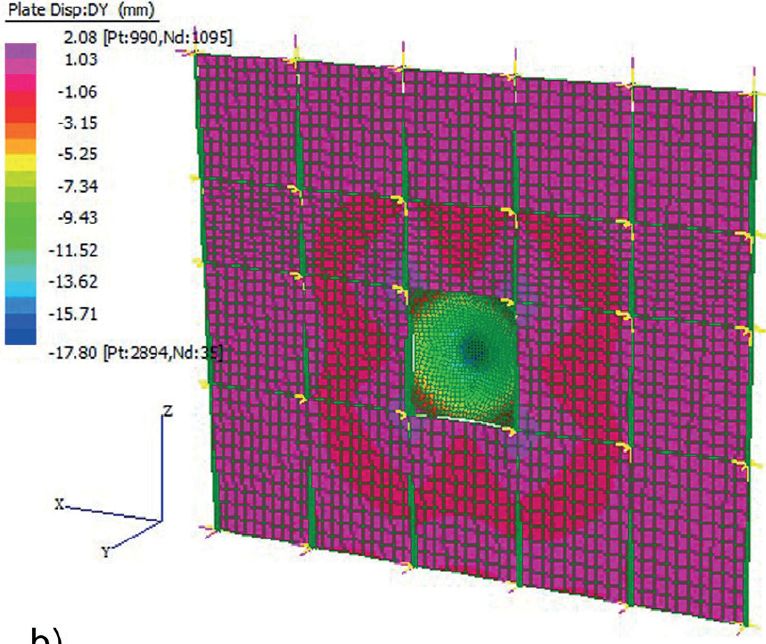
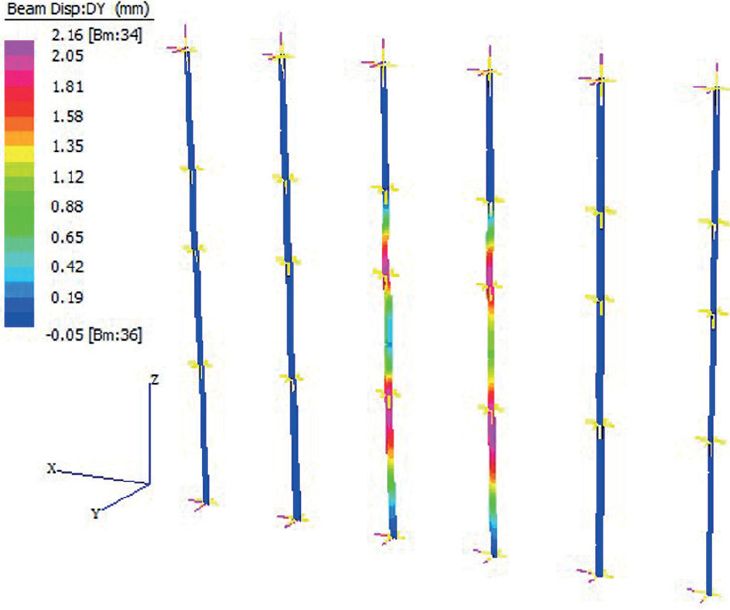
Nieprzeniesiona analiza dynamiczna, przeprowadzona w Straus7, zapewnia maksymalne pole przesunięcia poza płaszczyzną przedstawione na rys. 7b i maksymalne przemieszczenie kabli (rys. 7c), ale oprogramowanie może zapewnić całą historię czasu pod względem naprężeń i przemieszczeń.
Rys. 7. Dynamiczna analiza wykonana w Straus7 dla fasady z pojedynczym kablem.
a) układ,
b) maksymalne przesunięcie/przemieszczenie elementu poza płaszczyznę fasady,
c) przemieszczenia kabli podtrzymujących.
Interesujące może być porównanie uzyskanych właśnie wyników z wynikami pochodzącymi z nieliniowego podejścia energetycznego opisanego powyżej. Nieliniową sztywność panelu, w tym wpływ tylnej konstrukcji nośnej, oblicza się za pomocą modelu MES, przykładając rosnącą siłę skupioną w punkcie uderzenia (obszar odcisku nie zapewnia znacznych zmian przemieszczenia).
Następnie obliczany jest stan naprężeń a-posteriori (w następstwie). Obserwując wyniki zebrane w tabeli 2, można zauważyć, że podejście energetyczne przecenia o około 60% maksymalne przemieszczenia: dzieje się tak, ponieważ metoda ta nie uwzględnia wkładu bezwładności, który w omawianym przypadku może być znaczny, gdyż cała fasada, wspierana przez kable, uczestniczy w ruchu.
Ten sam wniosek dotyczy maksymalnego naprężenia rozciągającego, dla którego podejście energetyczne zapewnia wartości o około 50% wyższe niż w poprzedniej analizie ze Straus7. Chociaż podejście energetyczne jest zawsze po bezpiecznej stronie, przybliżenie z pewnością nie jest dokładne.
Podsumowując: ten przykład pokazuje potencjał proponowanego narzędzia skrzynki kontaktowej w analizie konstrukcji jako całości, zapewniając bardziej kompleksowy widok testu udarności.
Tabela 2. Podejście energetyczne w porównaniu z analizą dynamiczną w programie Straus7 przy użyciu narzędzii skrzynki kontaktowej

Wnioski
Standaryzowany test uderzenia ciałem miękkim w panele szklane został przeanalizowany teoretycznie. Jest to problem wartości nieograniczonych, ponieważ odcisk masy uderzającej, wykonanej z podwójnej opony pneumatycznej, zmienia się wraz z wypadkową siły nacisku.
Najpierw panel został zredukowany do prostego oscylatora liniowego przy użyciu modelu uderzającej opony uzyskanego poprzez sprężynę liniową i tłumienie w jednostronnym kontakcie, aby uwzględnić wielokrotne odbicia.
Porównanie z badaniami eksperymentalnymi potwierdziło dobrą zgodność, pomimo prostoty metody, dowodząc skutków tłumienia.
Ponadto obserwujemy, że sztywność panelu, zarówno w trybie liniowym, jak i (geometrycznym) nieliniowym, jest prawie niezależna od wielkości odcisku kontaktowego opony: pozwala to uznać panel za równoważny – sprężyna liniowa, której prawo konstytutywne można ocenić, zakładając stałą powierzchnię styku.
W praktycznych przypadkach bezwładność panelu można pominąć, tak że prosta równowaga energetyczna pozwala obliczyć wypadkową sił kontaktowych, na podstawie których można z kolei obliczyć a posteriori naprężenie i odkształcenie szkła.
Jednak tę metodę można zastosować tylko wtedy, gdy siły bezwładności są znikome. W celu dokładniejszych analiz przedstawiliśmy zaprojektowane narzędzie MES, które można wykorzystać w oprogramowaniu komercyjnym.
W rzeczywistości opiera się na modelu kontaktowym, wykonanym z nieliniowych elementów belkowych, aby indukować stały nacisk na pole eliptyczne, zmieniając się homotetycznie wraz z wypadkową sił kontaktowych. To narzędzie można zastosować do pełnego modelu prawdziwej struktury.
Proponowane podejście pozwala wstawić tłumienie, aby podążało za ruchem aż do całkowitego rozproszenia, i może rozważyć wiele zbiórek w razie potrzeby.
Zaimplementowane w Straus7 takie podejście zapewnia doskonałą zgodność z SJ Mepla w przypadkach, które to oprogramowanie może obsłużyć, zarówno w przypadku liniowym, jak i nieliniowym.
Następnie przetestowaliśmy jego potencjał dla pełnej fasady wspieranej przez proste kable, w których nieliniowości geometryczne mają ogromne znaczenie.
W tym przypadku każda analiza uwzględniająca izolowany panel nie może dać dokładnych wyników, ponieważ bezwładność całego układu bierze udział w ruchu. Testy eksperymentalne w celu potwierdzenia proponowanego podejścia będą przedmiotem przyszłych prac.
Alberto Consolaro Maffeis Engineering, Italy
Massimo Maffeis Maffeis Engineering, Italy
Gianmaria D’Ambrosio Department of Engineering and Architecture, University of Parma, Italy
Gianni Royer Carfagni ITC-CNR, Italy
Artykuł został oparty na wykładzie zaprezentowanym na Konferencji GLASS PERFORMANCE DAYS 2019, która odbyła się w dniach 26-28 czerwca 2019 r. Tampere w Finlandii
Bibliografia
[1] Anderson, C.E., Weiss, C.E., Chocron, S.: Impact Experiments Into Borosilicate Glass at Three Scale Sizes, J. Appl. Mech., 78, 051011/1-10 (2011)
[2] ANSYS,Theory Reference, Eigth Edition, SAS IP, Inc. (2000)
[3] Bohmann, I.D.: SJ Mepla Manual Theory, Version 3.5 (2012)
[4] Clough, R., Penzen, J.: Dynamics of structures, Second Edition, Mc Graw Hill International Editions, Civil Engineering Series (1993)
[5] DIN 18008-4: Glass in building-design and construction rules-part 4:additional requirements for barrier glazing. Din, Berlin, Germany
[6] EN 12600 Szkło w budownictwie - Badanie wahadłem - Udarowa metoda badania i klasyfikacja szkła płaskiego (Glass in building. Pendulum test. Impact test method and classification for flat glass), (2002)
[7] Freddi, F., Royer-Carfagni, G., Silvestri, M.: Full-Scale Experiments for Point- Fixing Frameless Laminated Glass, Int. J. Appl. Glass Sci. 1, 257-272 (2010)
[8] Galuppi, L., Manara, G., Royer-Carfagni, G.: Practical Expression for the design of laminated glass, Compos. part B-Eng. 45, 1677-1688 (2013)
[9] Mohagheghian, I., Wang, Y., Zhou, J., Guo, X., Charalambides, M.,
Yan, Y., Dear, J.: Soft impact response of laminated glass plates, 20th Conference on Composite Material, Copenhagen (2015)
[10] Pacios, A., Postigo, S., Huerta, C.: Relationship between characteristic parameters of impact test for safety glasses. Stahlbau, Spec. Issue March (2011)
[11] Royer-Carfagni, G., Silvestri, M.: An innovative point-fixing device for architectural glazing. From concept to realization, Glass Tech. Int. 20, 84-88 (2009)
[12] Royer-Carfagni, G., Silvestri, M.: Fail-safe Point fixing of structural glass. New advances, Eng. Struct. 31, 1661-1676, (2009)
[13] Schneider, J., Schula, S.: Two mechanical design concepts for simulating the soft body impact at glazings, Part 1, Numerical transient finite element simulation and simplified concept with equivalent static loads,” ICE publishing (2011)
[14] Schneider, J., Wormer, J.: Impact loading on glass panes by soft body impact – Theoretical analysis and experimental verification, Proceedings Glass Processing Days (2001)
[15] Shitanoki, Y., Bennison, S.J., Koike, Y.: Analytic Models of a Thin Glass-Polymer Laminate and Development of a Rational Engineering Design Methodology, J. Appl. Mech. 81, 121009/1-7 (2014)
Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 06/2020
































