
Współczesne budowle zachwycają nie tylko rozmiarami, ale również niespotykanymi dotąd rozwiązaniami konstrukcyjnymi oraz różnorodnością i innowacyjnym zastosowaniem materiałów.
W ostatnich dziesięcioleciach projektanci podjęli próbę zastosowania szkła jako materiału budującego elementy nośne.
Szkło znane od wielu stuleci przez długi okres stanowiło jedynie część okien. Od lat 60 ubiegłego wieku tafle szklane są pokryciem całych fasad wieżowców, a w ostatnich latach szklane belki i słupy zostały włączone w proces przenoszenia nie tylko ciężaru własnego, ale i obciążeń od innych elementów konstrukcji budynku.
Szkło materiałem konstrukcyjnym
Spośród wszystkich szeroko stosowanych materiałów konstrukcyjnych, tj. stali, betonu i drewna, wytrzymałość szkła oraz jego zachowanie w warunkach obciążenia zewnętrznego znane są najsłabiej.
Próbą upowszechnienia i ujednolicenia wiedzy o właściwościach szkła było opracowanie dokumentu European Standard EN 572, Glass in building 2004.
Dokument ten dotyczy jednak głównie elementów szklanych pracujących jak płyty w fasadach budynków, poddanych obciążeniom od ciężaru własnego i wiatru.
Wciąż jeszcze nie opracowano normy, która określałby warunki zniszczenia i sposoby badania wytrzymałości elementów szklanych pracujących jako belki czy słupy i przenoszących znacząco większe obciążenia niż ciężar własny.
Mimo intensywnych badań i szeroko dostępnej literatury dotyczącej właściwości szkła, materiał ten wciąż wydaje się być najtrudniejszym i najbardziej nieprzewidywalnym materiałem konstrukcyjnym.
Ta nieprzewidywalność zachowań szklanych elementów nośnych jest konsekwencją tego, że szkło jest materiałem kruchym, ulegającym zniszczeniu nagle i nie wykazującym żadnych odkształceń plastycznych.
Konwencjonalne kryteria zniszczenia materiałów kruchych
Najczęściej stosowane kryteria zniszczenia materiałów kruchych to kryterium największego naprężenia rozciągającego, kryterium największego odkształcenia oraz hipoteza Coulomba-Mohra.
Kryterium największego naprężenia rozciągającego wprowadzone zostało przez Galileusza.
Zakłada ono, że pęknięcie, a w konsekwencji zniszczenie materiału nastąpi w momencie miejscowego przekroczenia krytycznej, charakterystycznej dla danego materiału wartości naprężeń rozciągających. Hipoteza ta w latach późniejszych została rozwinięta przez Rankine i Clebscha i określona także dla naprężeń ściskających.
Kryterium największego odkształcenia głównego zastosowali po raz pierwszy Porcelet i Saint-Venant w połowie XIX w. W myśl tej hipotezy zniszczenie nie następuje, gdy odkształcenia główne materiału nie przekroczą pewnych, określonych wartości.
Podobnie jak w przypadku kryterium największego naprężenia, bezpieczne wartości odkształceń są ściśle określone dla każdego z materiałów.
Hipoteza zniszczenia Coulomba-Mohra, stosowana głównie w mechanice skał i gruntów przyjmuje, że zniszczenie materiału kruchego następuje w chwili przekroczenia przez naprężenia ścinające, występujące na danej powierzchni, pewnej krytycznej wartości, która zależy od naprężeń normalnych, prostopadłych do rozważanej powierzchni.
 Wyniki badania przeprowadzonych na szkle, jednoznacznie wskazują, że jest to materiał kruchy. Pozostaje pytanie, które z powyżej przytoczonych kryteriów zniszczenia można zastosować w celu określenia momentu zniszczenia elementu nośnego wytworzonego ze szkła.
Wyniki badania przeprowadzonych na szkle, jednoznacznie wskazują, że jest to materiał kruchy. Pozostaje pytanie, które z powyżej przytoczonych kryteriów zniszczenia można zastosować w celu określenia momentu zniszczenia elementu nośnego wytworzonego ze szkła.
Zawodność metod projektowania opartych o konwencjonalne kryteria zniszczenia materiałów kruchych
Przedstawione powyżej kryteria zniszczenia materiałów znalazły szerokie zastosowanie w procesie projektowania konstrukcji inżynierskich.
Liczne katastrofy obiektów, takich jak spawane mosty, tankowce i in. w latach 40. XX w. wykazały jednak, że istnieje wiele konstrukcji, dla których metody projektowania oparte na przytoczonych powyżej hipotezach wytrzymałościowych zawodzą.
Zostało udowodnione, że w pewnych warunkach i dla pewnych materiałów zniszczenie może nastąpić po osiągnięciu przez naprężenia rozciągające wartości dużo niższych, niż naprężenia krytyczne określane w hipotezach.
Już dziś wiadomo, że np. dla materiałów kruchych lub materiałów, które w pewnych warunkach zachowują się jak materiały kruche (np. stal w niskich temperaturach), 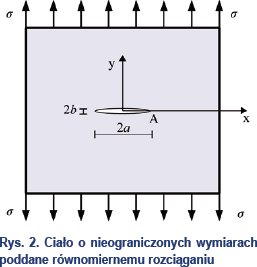 decydujące znaczenie dla nośności może mieć obecność uszkodzeń materiału, to jest spękań, pustek czy zarysowań powierzchni.
decydujące znaczenie dla nośności może mieć obecność uszkodzeń materiału, to jest spękań, pustek czy zarysowań powierzchni.
W klasycznych metodach projektowych, opartych na wytrzymałościowym kryterium naprężenia krytycznego, stosuje się współczynniki bezpieczeństwa zmniejszające wartość nośności materiału.
Ta redukcja nośności w stosunku do wartości nośności, którą podał producent materiału wynika właśnie z obecności wad materiałowych.
W przypadku materiałów kruchych, takich jak szkło, nie wykazujących prawie żadnych odkształceń plastycznych, pęknięcia występujące w elemencie powodują miejscowy wzrost naprężeń rozciągających do bardzo dużych wartości.
W analizie nośności takich materiałów zastosowanie współczynników bezpieczeństwa jest wielokrotnie niewystarczające do oceny naprężeń krytycznych.
Wiadomo, że raczej niemożliwe jest uniknięcie wprowadzania miejscowych uszkodzeń struktury elementu nośnego w procesie jego wytwarzania. Zdefiniowanie kryterium zniszczenia elementów wykonanych z materiałów o dużej wrażliwości nośności na obecność rys, wymaga sięgnięcia do wiedzy z zakresu mechaniki pękania.
Warunki pękania materiałów kruchych w ujęciu mechaniki pękania
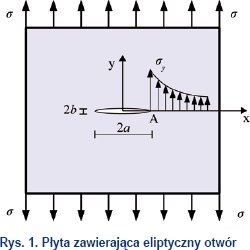
W 1913 r. Inglis przeprowadził próbę określenia naprężeń w rozciąganej jednorodnie płycie, zawierającej eliptyczny otwór (rys. 1).
Analiza wykazała, że wartość naprężeń w okolicach wierzchołka otworu przekracza wielokrotnie wartość obciążeń, którym poddana została płyta.
Inglis podał, że naprężenia w punkcie A wynoszą:
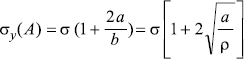
gdzie ρ oznacza promień krzywizny elipsy
w punkcie A i
![]()
Badania Griffitha zniszczenia materiałów kruchych
W 1920 roku w Philosophical Transactions of the Royal Society of London opublikowany został artykuł A. A. Griffitha The phenomenona of rupture and flow in solids.
Praca ta poprzedzona była licznymi badaniami wytrzymałościowymi 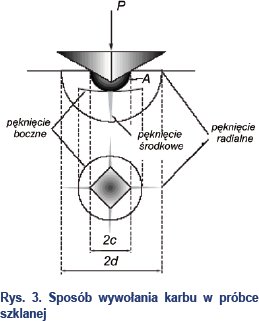 przeprowadzonymi na włóknach i płytach szklanych. Wyniki badań skłoniły A. A. Griffitha do stwierdzenia, że zarówno makroskopowe jak i mikroskopowe pęknięcia mogą być potencjalnym źródłem osłabienia materiału, gdyż każda nieciągłość struktury wewnętrznej jest koncentratorem naprężeń, jak wykazał Inglis.
przeprowadzonymi na włóknach i płytach szklanych. Wyniki badań skłoniły A. A. Griffitha do stwierdzenia, że zarówno makroskopowe jak i mikroskopowe pęknięcia mogą być potencjalnym źródłem osłabienia materiału, gdyż każda nieciągłość struktury wewnętrznej jest koncentratorem naprężeń, jak wykazał Inglis.
Koncentrację naprężeń wywołują zatem zarówno defekty nie związane ze budową materiału (wszelkie wady geometryczne czyli szczeliny oraz wcięcia – karby o dowolnej geometrii) jak wady budowy wewnętrznej materiału (pustki rozlokowane wzdłuż granic ziaren, wtrącenia obcego materiału itp.)
Właśnie obecnością takich defektów w strukturze ciała stałego Griffith tłumaczył rozbieżność między wartościami wytrzymałości praktycznej materiału a wytrzymałością teoretyczną. Przez pojęcie wytrzymałości teoretycznej rozumie się największe naprężenie, jakie może przenieść materiał, bez przerwania połączeń między atomami.
Kryterium Griffitha zniszczenia materiałów kruchych
Opisanie procesu zniszczenia materiału w procesie pękania wymaga rozważań w skali mikro jak i w skali makro, i jest możliwe tylko dzięki zastosowaniu zasad mechaniki kwantowej oraz zasad mechaniki continuum. Kiedy ciało stałe pęka tworzą się dwie nowe powierzchnie w ośrodku. Jest to proces termodynamiczny, nieodwracalny.
Pęknięcie materiału spowodowane jest rozerwaniem połączeń atomowych w konsekwencji wystąpienia naprężeń lokalnych o wartościach krytycznych. Badania Griffitha skłoniły go do poszukiwania kryterium, pozwalającego na określenie warunków zniszczenia materiałów wrażliwych na obecność defektów materiałowych.
Kryterium Griffitha określające moment inicjacji wzrostu pęknięcia w ciele, zostało określone w oparciu o bilans energetyczny zapisany dla ciała zawierającego szczelinę.
![]()
gdzie L oznacza pracę wykonaną w jednostce czasu przez obciążenia zewnętrzne, E oznacza prędkość zmian energii wewnętrznej ciała, K oznacza prędkość zmian energii kinetycznej ciała,
W oznacza ilość energii zużytej w jednostce czasu na utworzenie jednostki powierzchni szczeliny. Po licznych przekształceniach i podstawieniach ostatecznie otrzymujemy kryterium zniszczenia materiału kruchego Griffitha.
G = GC
Zgodnie z tym kryterium do wzrostu pęknięcia dochodzi wówczas, gdy zmiana energii potencjalnej G (energii zużytej na wzrost pęknięcia) ciała ze szczeliną jest co najmniej równa odporności materiału na pękanie GC = 2γ, przy czym γ oznacza właściwą energię powierzchniową, czyli energię potrzebną do rozerwania połączeń między atomami.
Krytyczne obciążenie płyty wynikające z kryterium Griffitha
Równanie G = 2γ pozwala na wyznaczenie wartości obciążenia krytycznego, czyli takiego, przy którym szczelina zaczyna się powiększać. Rozważmy ciało o nieograniczonych wymiarach, zawierające szczelinę o długości 2a i poddane równomiernemu rozciąganiu prostopadle do długości szczeliny.
Dla tego typu obciążenia szczeliny wartość obciążenia krytycznego wyraża się następująco:
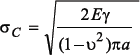
dla płaskiego stanu odkształceń
![]()
dla płaskiego stanu naprężeń.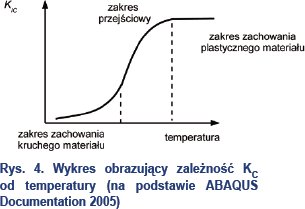
Powyższe równania są prawdziwe przy założeniu, że odporność na pękanie ciała jest wielkością stałą.
To założenie spełniają materiały, w których odkształcenia plastyczne są bardzo małe, a inicjacja szczeliny jest równoważna z jej lawinowym, niekontrolowanym powiększaniem się, prowadzącym do zniszczenia próbki. Założenie to spełnia szkło, zatem przy określaniu wartości naprężeń krytycznych dla tego materiału można stosować powyższe wzory.
Siłowe kryterium pękania
Energetyczne kryterium pękania przedstawione równaniem G = 2γ jest często zastępowane równoważnym siłowym kryterium pękania, które nie wymaga znajomości wielkości energii powierzchniowej, trudnej do wyznaczenia drogą doświadczalną.
W kryterium siłowym rezygnuje się z zastosowania energii powierzchniowej jako miary odporności na pękanie i wprowadza się nową, charakterystyczną dla danego materiału wielkość, nazywaną krytycznym współczynnikiem intensywności naprężeń KIC.
Kryterium siłowe nazywane również kryterium krytycznego współczynnika intensywności naprężeń, mówi, że zniszczenie elementu w wyniku pęknięcia nastąpi w momencie, w którym wartość współczynnika koncentracji naprężeń osiągnie pewną wartość krytyczną:
KI = KIC
gdzie KI to współczynnik intensywności naprężeń, KIC jest stałą materiałową określaną jako wytrzymałość na pękanie i wyznaczaną eksperymentalnie. Wartość współczynnika KIC określone są następująco:
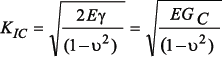
dla płaskiego stanu odkształceń ![]() dla płaskiego stanu naprężeń
dla płaskiego stanu naprężeń
Metoda wyznaczania wartości wytrzymałości na pękanie KIC dla szkła
Istnieje wiele metod wyznaczania KIC dla szkła. Wśród nich jest jedna, według której wartość krytyczną współczynnika intensywności naprężeń można określić bez potrzeby określania długości szczeliny a.
Metoda ta polega na zginaniu próbki szklanej, której krawędź zawiera karb. Karb (wgniecenie) wykonuje się za pomocą diamentowego ostrosłupa foremnego o podstawie kwadratowej.
Według opisywanej metody wartość KIC jest określona następującą zależnością:
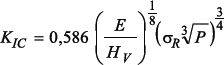
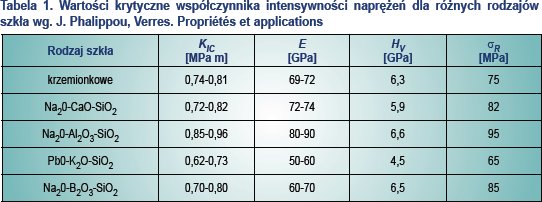
gdzie HV - jest mikro twardością Vickersa dla szkła, σR - naprężenie niszczące, P – siła potrzebna do wytworzenia karbu, E – moduł Younga materiału.
Wyznaczone doświadczalnie wartości krytycznych współczynników intensywności naprężeń dla różnych rodzajów szkła zestawiono w tabeli 1.
Zależność odporności na pękanie KIC od temperatury i grubości elementu
Jak wykazały doświadczenia krytyczna wartość współczynnika koncentracji naprężeń KIC ulega zmianie w zależności od temperatury i grubości elementu zbudowanego z danego materiału.
Z rys. 4 wynika, że w procesie projektowania elementów z danego materiału należy uwzględnić temperaturę, w jakiej dany element będzie się znajdował i określić jej wpływ na wartość wytrzymałości na pękanie.
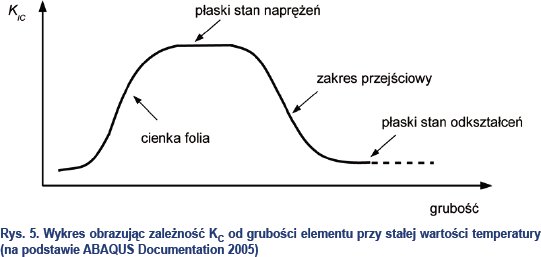
Rys. 5 pokazuje, że minimalne wartości wytrzymałości na pękanie otrzymuje się w płaskim stanie odkształcenia. Wyznaczony w tym stanie współczynnik KIC jest uznawany za charakterystykę materiałową i pełni on analogiczną rolę, jak np. wytrzymałość na rozciąganie w pręcie rozciąganym w tradycyjnie rozumianej wytrzymałości materiałów.
Kryterium Rice’a
W 1968 roku Rice wprowadził nową postać kryterium pękania, wyrażoną za pomocą całki J. Całka J służy do określenia ilości energii uwalnianej w czasie wzrostu pęknięcia. Zgodnie z kryterium Rice’a wzrost pęknięcia i w konsekwencji zniszczenie materiału nastąpi, gdy wartość całki Rice’a J osiągnie wartość krytyczną JC.
J=JC
Wielkość JC jest stałą materiałową. Jej wartość można wyrazić za pomocą opisanej wcześniej wielkości krytycznego współczynnika intensywności naprężeń KIC:
![]()
dla płaskiego stanu odkształceń ![]()
dla płaskiego stanu naprężeń.
Artykuł powstał na podstawie pracy magisterskiej „Warunki pękania i zniszczenia szkła” napisanej pod kierunkiem prof. dr. hab. inż. Tomasza Łodygowskiego i dr. inż Witolda Kąkola w Zakładzie Komputerowego Wspomagania Projektowania Politechniki Poznańskiej
- Łączniki punktowe w szklanych konstrukcjach , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 1/2009
- Projektowanie szklanych konstrukcji mocowanych punktowo , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 2/2009
- Badanie doświadczalne konstrukcji szklanych mocowanych punktowo , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 3/2009
- Analiza numeryczna konstrukcji szklanych mocowanych punktowo cz. 1 , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 4/2009
- Analiza numeryczna konstrukcji szklanych mocowanych punktowo cz. 2 , Barbara Szczerbal, Dariusz Włochal, Adam Glema, Tomasz Łodygowski , Świat Szkła 6/2009
inne artykuły o podobnej tematyce patrz Serwisy Tematyczne































