Jak wiadomo, kontrola wymiany ciepła jest niezwykle istotna dla naprężeń wewnętrznych powstających w jej wyniku. Hartowanie szkła cienkiego stało się źródłem nowych wyzwań, nie tylko w zakresie równomiernej wymiany ciepła, lecz także zużycia energii, ponieważ w procesie tym współczynniki wymiany ciepła muszą być bardzo wysokie.
Do chłodzenia wykorzystywane są niewielkie strumienie powietrza o dużej prędkości, ustawione blisko powierzchni szkła, co powoduje dużą zmienność miejscowego współczynnika wymiany ciepła. Jednocześnie dochodzi do anizotropii optycznej przybierającej formę pasów lub punktów na powierzchni szkła.
Nie jest możliwe uniknięcie tego zjawiska w każdych warunkach oświetlenia i z każdej perspektywy, nawet jeśli chłodzenie odbywa się równomiernie. Jednak z pewnością nierównomierność samego procesu obniżania temperatury potęguje ten efekt.
Wstęp
W niniejszym artykule zaprezentowano wyniki miejscowej wymiany ciepła obliczone numerycznie (metodą obliczeniowej mechaniki płynów CFD) dla „uderzających” strumieni powietrza. Posłużyły one za dane wyjściowe w modelowaniu numerycznym naprężeń wewnętrznych. Przeanalizowano przypadek kontrolny w celu sprawdzenia zarówno wymiany ciepła, jak i naprężeń wewnętrznych.
Wyniki rozkładu naprężeń wewnętrznych zostały następnie porównane z rozkładem anizotropii zachodzącej na warstwach ze szkła hartowanego, które zostały zbadane przy użyciu polaryskopu.
Wymiana ciepła jest podstawą w procesie hartowania szkła, które jest w pierwszej kolejności nagrzewane do temperatury przekraczającej 600°C, a następnie w kilka sekund chłodzone do temperatury poniżej 450°C w celu wytworzenia w szybie naprężeń wewnętrznych. Profil naprężeń wygląda następująco: warstwy powierzchniowe są poddawane ściskaniu (kompresji) – występują w nich naprężenia ściskające, natomiast w warstwie wewnętrznej powstają naprężenie rozciągające.
Przed ochłodzeniem szkło musi zostać rozgrzane do odpowiedniego poziomu. Zbyt wysoka temperatura może doprowadzić do powstania efektu falowania szkła lub innych, miejscowych wad w postaci wygięcia materiału. Natomiast zbyt niska temperatura uniemożliwia powstanie naprężeń wewnętrznych [1]. Niejednorodne pole temperatury może doprowadzić do różnych wad w postaci wygięcia szkła lub też spowodować nierównomierny rozkład naprężeń na jego powierzchni.
Szybkość chłodzenia musi być wysoka, tak by możliwe było wystarczająco szybkie obniżenie temperatury szkła, co w efekcie sprawi, że wytworzony zostanie odpowiedni poziom naprężeń wewnętrznych. W celu wyprodukowania wizualnie ładnego szkła proces chłodzenia musi być również relatywnie równomierny.
Spolaryzowane światło słoneczne, zarówno padające bezpośrednio z bezchmurnego nieba, jak i odbite, może uwidocznić niejednakową jakość szkła w postaci wizualnego efektu nazywanego anizotropią. W kontekście przemysłowym badanie tafli szklanych może zostać przeprowadzone przy użyciu polaryskopu [2].
Na rys. 1 pokazano skrajne przypadki anizotropii optycznej na szklanej tafli ze szkła hartowanego. Podobny efekt wizualny można zaobserwować na tylnych szybach samochodowych, patrząc przez okulary przeciwsłoneczne z polaryzacją. Takie zjawisko anizotropii wynika z nieruchomego ustawienia chłodzących strumieni powietrza. Przykład zwykłego szkła hartowanego, które zostało poddane chłodzeniu poprzez przesuwanie, znajduje się na rys. 2.
Wiadomo, że nierównomierna wymiana ciepła powoduje nierównomierne naprężenia wewnętrzne, co w efekcie prowadzi do powstania efektu anizotropii. Szczegóły tego mechanizmu nie zostały jednak jeszcze dobrze poznane.
W zależności od poziomu anizotropii, jakość wizualna szkła hartowanego może być dobra lub zła. Także usytuowanie elementów szklanych oraz ilość spolaryzowanego światła w danym miejscu ma wpływ na skalę widocznych wad.
W procesie hartowania system dysz chłodzących może składać się z tysięcystrumieni, które powinny być rozłożone w sposób umożliwiający względnierównomierną wymianę ciepła na powierzchni. Jednak, najwyższy poziom wymiany ciepła notowany jest w punkcie „zastoju” strumienia, natomiast im dystans od punktu „stagnacji” jest większy tym mniejszy jest poziom wymiany ciepła [3].
W trakcie procesu chłodzenia szkło najpierw zostaje przeniesione z części nagrzewającej do części chłodzącej, w której wskaźniki miejscowej wymiany ciepła zmieniają się z upływem czasu w każdym miejscu na powierzchni szkła. Zmiana pozycji względem dysz sprawia, że wymiana ciepła jest dużo bardziej równomierna na powierzchni i w czasie.
Dzięki ruchowi miejscowe naprężenie nie zmienia się znacznie w kierunku przesuwania się szkła. Jednak naprężenia prostopadłe do kierunku ruchu szkła ulegają zmianie, ze względu na różnice w miejscowej wymianie ciepła. Ta nierównomierność wymuszonej konwekcji w trakcie hartowania powoduje powstanie pasów wzdłuż kierunku przesuwania się szkła.
Równomierny rozkład naprężenia jest szczególnie ważny w przypadku szkła przeznaczonego do wykorzystania w architektonicznie prestiżowych budynkach, ponieważ światło spolaryzowane występuje w normalnym świetle dziennym.
W artykule zbadano wpływ miejscowej wymiany ciepła inicjowanej „uderzającymi” strumieniami powietrza na powierzchniową wymianę ciepła oraz naprężenia wewnętrzne.
Współczynniki konwekcji dla powietrza (według modelu cieczy) zostały obliczone przy użyciu otwartego oprogramowania CFD firmy OpenFOAM. Rozkład temperatur w szkle oraz naprężenia wewnętrzne zostały
Jak wiadomo, kontrola wymiany ciepła jest niezwykle istotna dla naprężeń wewnętrznych powstających w jej wyniku. Hartowanie szkła cienkiego stało się źródłem nowych wyzwań, nie tylko w zakresie równomiernej wymiany ciepła, lecz także zużycia energii, ponieważ w procesie tym współczynniki wymiany ciepła muszą być bardzo wysokie.
Do chłodzenia wykorzystywane są niewielkie strumienie powietrza o dużej prędkości, ustawione blisko powierzchni szkła, co powoduje dużą zmienność miejscowego współczynnika wymiany ciepła. Jednocześnie dochodzi do anizotropii optycznej przybierającej formę pasów lub punktów na powierzchni szkła.
Nie jest możliwe uniknięcie tego zjawiska w każdych warunkach oświetlenia i z każdej perspektywy, nawet jeśli chłodzenie odbywa się równomiernie. Jednak z pewnością nierównomierność samego procesu obniżania temperatury potęguje ten efekt.

Rys. 1. Zjawisko anizotropii na szkle hartowanym bez znaczącego ruchu tafli szkła w trakcie hartowania – widok przez filtry polaryzacyjne

Rys. 2. Zjawisko anizotropii na szkle hartowanym z widocznym wpływem ruchu w trakcie hartowania – widok przez filtry polaryzacyjne
(...)
(...)
wyliczone z wykorzystaniem metody elementów skończonych i oprogramowania Ansys. Uzyskane współczynniki wymiany ciepła zostały porównane z pomiarami dla pojedynczego strumienia powietrza w celu sprawdzenia dokładności modelowania.
Numerycznie uzyskane współczynniki konwekcji wykorzystano w modelowaniu prawdziwej linii do hartowania szkła z różnymi ustawieniami strumieni powietrza. Na koniec, rozkład naprężeń wewnętrznych został porównany z rozkładem śladów na szkle powstałych w wyniku anizotropii zachodzącej na warstwach ze szkła hartowanego. Do tego badania użyto polaryskopu.
Wymiana ciepła
W celu określenia rozkładu naprężeń wewnętrznych w warstwie szkła, w pierwszej kolejności należy wyliczyć rozkład temperatur w tej warstwie. Założono, że szkło ma stałą temperaturę wyjściową przed chłodzeniem. W artykule przedstawiono jedynie wyliczenia dotyczące chłodzenia w procesie hartowania.
W przypadku chłodzenia znaczenie mają dwa czynniki: przewodzenie ciepła wewnątrz szkła oraz konwekcja ciepła pomiędzy powierzchnią szklaną a powietrzem. W obu przypadkach w celu oszacowania wartości wykorzystano metody numeryczne oraz uwzględniono miejscowe i tymczasowe zmiany w wymianie ciepła.
Przewodzenie warstwy szklanej
Rozkład temperatur oraz historia zmian termicznych w warstwie szklanej bez wewnętrznych źródeł ciepła obliczane są przy użyciu następującego równania:
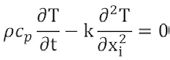 (1)
(1)
w którym właściwości termiczne szkła, tj. gęstość ρ, ciepło właściwe cp oraz przewodnictwocieplne k są zależne od temperatury i przebiegają jednokierunkowo.
Efekt promieniowania w równaniu 1 w trakcie chłodzenia jest niewielki i nie został uwzględniony. W celu rozwiązania powyższego równania przewodzenia ciepła, należy najpierw określić współczynnik konwekcji powietrza (według modelu cieczy) na powierzchni szkła poprzez założenie, że współczynnik wymiany ciepła oraz temperatura powierzchni szkła nie są sprzęgnięte
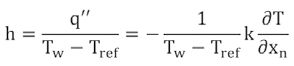 (2),
(2),
gdzie xn to normalny kierunek powierzchni, Tw i Tref to temperatura powierzchni oraz temperatura chłodzącego powietrza. Współczynnik wymiany ciepła, z równania (2), zapewnia warunki brzegowe dla równania (1) i jest wyliczany według modelu turbulencji k-ω-SST uwzględnionej w kolejnej części.
Równanie (1) jest rozwiązywane przy użyciu metody elementów skończonych za pomocą programu Ansys 17 [4]. Uderzenie cieplne jest wyliczane na podstawie równania zachowania energii wg metody obliczeniowej mechaniki płynów (patrz następna część opracowania).
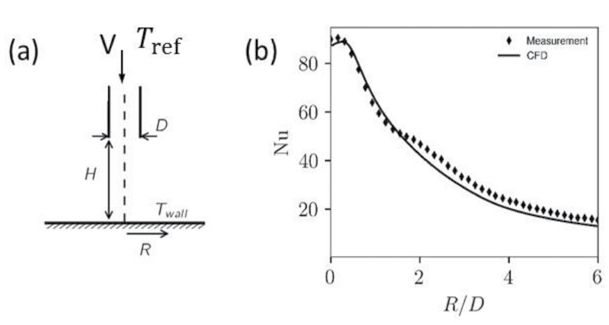
Rys. 3. Schemat dyszy (a) i porównanie numerycznie modelowanej i pomiarowej liczby Nusselta Nu=hD/ka (b)
Konwekcja pomiędzy szkłem a powietrzem
Konwekcja wyliczana jest przy użyciu metody elementów skończonych z wykorzystaniem otwartego oprogramowania OpenFOAM [5]. Dokładność obliczeń została sprawdzona poprzez porównanie wyników z danymi eksperymentalnymi uzyskanymi dla pojedynczego strumienia powietrza (rys. 3b).
Test ten został wybrany z artykułu Alimohammadi’ego [6]; przyjęto następujące wartości: Re=14000, H/D=4, and D=13 mm. Liczba Nusselta wynosi Nu=hD/ka, gdzie h jest współczynnikiem konwekcji cieczy, D jest średnicą dyszy, a ka jest przewodnictwem cieplnym powietrza.
Na rys. 3 przedstawiono wyniki oraz schematyczną ilustrację układu dysza- płaszczyzna. Stosunek wysokości dyszy do jej średnicy H/D jest zgodny z tą wykorzystaną do hartowania. Liczba Reynoldsa Re=VD/v, gdzie V oznacza prędkość przepływu, D jest średnicą dyszy a v to lepkość kinetyczna powietrza, jest mniej więcej równa połowie wartości wykorzystanej w procesie hartowania.
Warto zauważyć, że dzięki metodzie obliczeniowej mechaniki płynów (CFD) możliwe jest bardzo precyzyjne przewidywanie wymiany ciepła. Wszystkie obliczone numerycznie liczby Nusselta mieszczą się w zakresie 15% wartości pomiarowych.
Wskaźniki konwekcji przyjęte w niniejszym artykule w celu modelowania naprężenia szczątkowego opracowano przy użyciu modelu 3D. Układ strumieni powietrza w części chłodzącej składa się z powtarzających się serii i w wyliczeniach należy uwzględnić jedynie jedną z nich.
Powierzchnia szkła ma stałą temperaturę 500°C, mniej więcej równą średniej przedmiotowego zakresu temperatur szkła przeznaczonego do hartowania. Żadne funkcje ścian nie mają zastosowania dla powierzchni szklanych, ponieważ nie są odpowiednie dla przepływów uderzających strumieni.
Równania Naviera-Strokesa dla przepływu ściśliwego w stanie ustalonym są rozwiązywane przy użyciu metody uśredniania Reynoldsa dla turbulencji. Do obliczenia energii kinetycznej turbulencji wykorzystano model Mentera k-ω-SST [7]
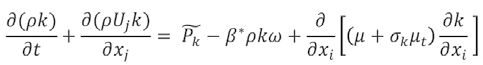 (3)
(3)
A współczynnik dyssypacji (rozpraszania) energii właściwy został wyliczony na podstawie równania
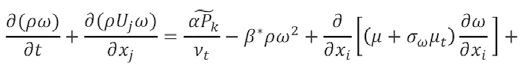
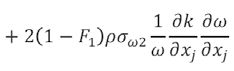 4)
4)
Model wykorzystywany w OpenFoam 4.0 [5] różni się szczegółami od tego zaproponowanego przez Mentera [7].
Szczegóły podano w kodzie źródłowym OpenFoam, a także w artykule autorstwa Mikkonena i Karvinena [8].
Wykorzystanym równaniem stanu jest równanie Clapeyrona, a z wzoru Sutherlanda skorzystano, by wyliczyć lepkości w celu uwzględnienia wpływu temperatury. Konwekcja ciepła na powierzchni szkła jest w dużej mierze uzależniona od rozmiaru i jakości siatki dysz. Bardzo gęsta siatka wykorzystywana jest blisko powierzchni szkła.
Stopień niezależności siatki jest badany poprzez zwiększanie jej gęstości. W przypadku wyliczeń 3D potrzebnych jest miliony ogniw. Więcej informacji wprowadzających do tematu wymiany ciepła z wykorzystaniem uderzających strumieni można znaleźć w artykule Zuckermana i Liora [9].
Naprężenie wewnętrzne
Wyliczenie naprężeń wewnętrznych powstałych w wyniku procesu hartowania opiera się na modelu termomechanicznym. W przypadku naprężeń termicznych do określenia rozkładu temperatur konieczne jest wykorzystanie teorii przedstawionej w punkcie 2.1 powyżej.
Zachowanie mechaniczne szkła w procesie chłodzenia jest uzależnione od odkształceń termicznych oraz lepkosprężystości szkła w różnych temperaturach. Naprężenie szkła w dowolnym momencie można obliczyć korzystając z równania (5) [10].
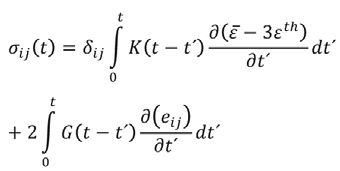 (5)
(5)
Gdzie σij to naprężenie główne, K(t) to moduł relaksacji objętościowej, jak pokazano w równaniu (6), G(t) jest modułem relaksacji odkształcenia, jak pokazano w równaniu (7), Σ to składowe odkształceń zgodnie z równaniami (8) i (9), a Σth to odkształcenie termiczne, zgodnie z równaniem (10). W modelu mechanicznym uwzględniono termicznie uzależnioną lepkoelastyczność oraz relaksację strukturalną [11].
W obliczeniach wykorzystano oprogramowanie Ansys 17.0 [4], które oparte jest na metodzie elementów skończonych MES (finite element method FEM). Wyliczeń naprężeń wewnętrznych należy dokonać w przebiegu przejściowym w różnych odstępach czasu przez cały okres chłodzenia. Weryfikację modelu przeprowadził Aronen w swojej pracy [12], a porównanie z wynikami eksperymentalnymi zostało wykonane przez Gardona [13] (rys. 4).
W obu przypadkach wykorzystano jednakowe współczynniki wymiany ciepła na całej powierzchni. Wyniki modelowania są takie same jak wyniki eksperymentu, w którym przyjęto niski współczynnik wymiany ciepła. Jednak w przypadku wysokiego współczynnika wymiany ciepła wyniki w modelu są o około 10% niższe niż wyniki otrzymane w eksperymencie. Warto zauważyć, że pomiary naprężeń wewnętrznych nie są proste do wykonania i mogą być obciążone błędem.
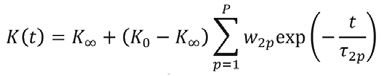 (6)
(6)
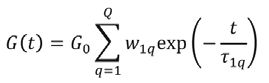 (7)
(7)
gdzie indeks dolny równy 0 jest wartością początkową, a ∞ oznacza wartość w nieskończoności.
W przypadku współczynnika wagi (ważności) w oraz czasów relaksacji τ, index 1 odpowiada relaksacji odkształcenia a 2, relaksacji objętościowej.
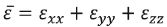 (8)
(8)
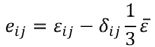 (9)
(9)
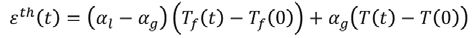 (10)
(10)
gdzie αl jest współczynnikiem rozszerzalności cieplnej dla stanu ciekłego, natomiastn αg współczynnikiem rozszerzalności cieplnej dla stanu szklistego. Temperatura zeszklenia Tf jest powiązana z relaksacją struktury szkła [11]. Szczegółowa teoria odnosząca się do tego modelu została już opisana w literaturze [12].
Anizotropia
Zjawisko anizotropii można wyjaśnić posługując się różnicami w naprężeniach głównych. W celu wskazania metodą eksperymentalną pola naprężeń w materiałach przezroczystych wykorzystano elastooptykę. Zgodnie z regułami elektrooptycznymi główne czynniki załamania światła wyrażone są w postaci funkcji naprężeń głównych. Współczynnik załamania w kierunku 1 zaprezentowano w równaniu (11). Równania dla innych kierunków są takie same za wyjątkiem indeksów dolnych w oznaczeniach [14].
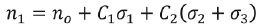 (11)
(11)
Parametr n0 to współczynnik załamania światła materiału nienaprężonego, a stałe C1 oraz C2 są uzależnione od materiału. W przypadku płaskiego stanu naprężenia warstwa szklana poddawana jest naprężeniu normalnemu, i przechodzi przez nią światło w kierunku 3. Następnie sprawdzana jest różnica naprężeń σ1- σ2.
Opóźnienie względne δ zostało wyrażone równaniem prawa Wertheima i zostało podane przez Abena i Guillemeta [14]. Gdzie C=C1-C2 jest stałą elastoplastyczną, a d to grubość materiału. W przypadku gdy rozkład naprężeń zmienia się w zależności od grubości, względne opóźnienie może być ujednolicone na całej powierzchni [14].
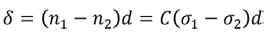 (12)
(12)
Zgodnie z graficzną prezentacją na rys. 5, w celu zobrazowania kolorowego wzoru powstającego w wyniku zjawiska anizotropii można wykorzystać polaryskop płaski. Światło polaryskopu ulega w pierwszej kolejności polaryzacji na filtrze polaryzującym.
Spolaryzowane światło przechodzi przez szkło, w którym występują naprężenia wewnętrzne i dochodzi na nim do względnego przesunięcia fazowego składowych światła spolaryzowanego. Na koniec, spolaryzowane światło z względnym przesunięciem fazowym przechodzi przez drugi filtr polaryzujący, który jest obrócony względem pierwszego filtra o 90°.
 (13)
(13)
Wyniki obliczeniowe i pomiarowe dla szkła hartowanego
Konwekcja ciepła w przypadku hartowania
Współczynniki wymiany ciepła zostały obliczone przy użyciu geometrii dysz wykorzystywanych w części chłodzącej urządzenia do hartowania szkła (rys. 6).
Nadciśnienie wynosi 5000 Pa w porównaniu do zewnętrznego ciśnienia atmosferycznego, prędkość strumieni to około V≈100 m/s, H/D≈4, a D≈5 mm.
Wykorzystane metody numeryczne zostały opisane powyżej w punkcie Konwekcja pomiędzy szkłem a powietrzem, a oczekiwania w stosunku do geometrii i nadciśnienia są takie same, jak w przypadku kontrolnym z rys. 3. Całkowita długość płytki dyszy wynosi 80 mm. Płytki zostały rozstawione co 120 mm.
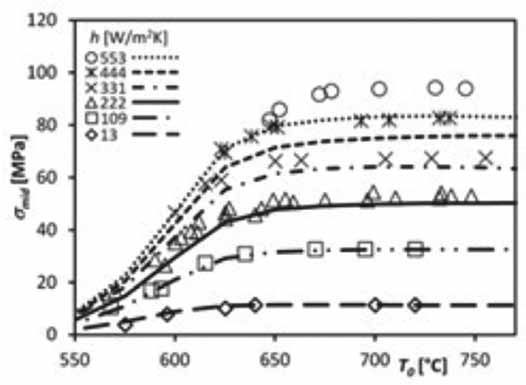
Rys. 4. Porównanie wyników eksperymentu (widoczne jako punkty [13]) oraz wyliczonych na podstawie modelu (widoczne jako linie [12]) naprężeń wewnętrznych w płaszczyźnie środkowej z różnymi temperaturami wyjściowymi oraz współczynnikami wymiany ciepła.
Grubość szkła wynosi 6,1 mm
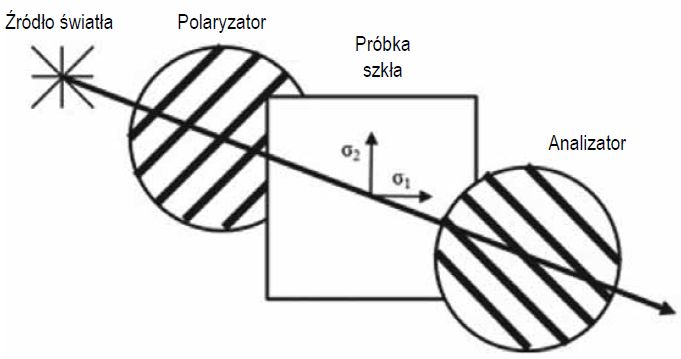
Rys. 5. Ilustracja polaryskopu
Na rys. 7 przedstawiono współczynnik wymiany ciepła na powierzchni szkła, otrzymany w wyniku obliczeń. Można zauważyć, że wymiana ciepła zestawu dysz jest podobna jakościowo do wymiany ciepła pojedynczej dyszy zilustrowanej na rys. 3. Wymiana ciepła jest najwyższa w pobliżu punktu stagnacji, w miejscu, w którym strumienie uderzają bezpośrednio w powierzchnię szkła, a spada w momencie zwiększenia odległości od punktu stagnacji.
Współczynniki wymiany ciepła z rys. 7 wykorzystano w celu obliczenia pola temperatur przesuwającego się szkła, a wpływ lokalizacji strumieni został opisany w dalszej części artykułu. Wymiana ciepła jest niska pod rolkami nośnymi w pobliżu krawędzi obszaru obliczeń w kierunku y ze względu na niemal zerową prędkość powietrza. Nieregularności w polu są spowodowane przejściowym charakterem strumieni.
Rozkład naprężeń wewnętrznych w szkle
Rozkład naprężeń w szkle po procesie hartowania został wyliczony z wykorzystaniem rozkładu współczynników konwekcji obliczonych powyżej i zilustrowanych na rys. 7.
Rozkład naprężeń został określony dla trzech różnych sytuacji. W pierwszym przypadku (C1) obliczony rozkład miejscowej wymiany ciepła powtarza się cyklicznie. W drugim przypadku (C2) sekwencje rozkładu wymiany ciepła są przesunięte w kierunku x o połowę szerokości pojedynczego cyklu.
W trzecim przypadku (C3) sekwencje są przesunięte w kierunku x o jedną czwartą szerokości pojedynczego cyklu. Powyższe przypadki zostały zilustrowane na rys. 8. Szerokość kolejnych cykli wynosi 40 mm, a długość 120 mm.
W modelu szkło grubości 3,85 mm jest przesuwane względem systemu hartowania nieprzerwanie w jednym kierunku (w kierunku y) przez 5 s, z prędkością 450 mm/s. Odpowiada to przesunięciu szkła wzdłuż agregatu chłodniczego o długości 2 m.
Po 5 sekundach chłodzenie zastąpiono jednakowym współczynnikiem wymiany ciepła (330 W/m2K) i zakończyło się zarówno chłodzenie, jak i ruch szkła. Szkło zostało schłodzone do temperatury zbliżonej do temperatury pokojowej. Zmiana w jednakowy współczynnik wymiany ciepła została wprowadzona w celu uproszczenia wyliczeń.
Początek chłodzenia jest najważniejszy, a zmiana po 5 s nie wpływa na rozkład naprężeń wewnętrznych. Wymiana ciepła jest symetryczna do płaszczyzny środkowej. Rozmiar modelowego obszaru, w którym brane pod uwagę są naprężenia wewnętrzne, to 100x100 mm2, co zostało zilustrowane na rys. 9.
Początkowa temperatura szkła wynosi 650°C. Istotne właściwości szkła wykorzystanego w modelu są analogiczne do tych zastosowanych przez Aronena [12]. Wyniki pokazują, że naprężenie na obszarze 40x40 mm2 , w samym środku obszaru modelowego, znacznie różni się jedynie w kierunku x, co zostało pokazane na rys. 10.
Zróżnicowanie naprężeń ma miejsce ze względu na miejscowe wahania średniej wymiany ciepła. Naprężenie w kierunku x, jak i w kierunku y, podobnie jak różnica naprężeń wzdłuż w kierunku x z innym układem dysz na powierzchni oraz na płaszczyźnie środkowej zilustrowano na rys. 11 (powierzchnia) oraz 12 (płaszczyzna środkowa).
Naprężenia te zakreślają krzywą wzdłuż przerywanej linii pokazanej na rys. 10. Wyniki ilustrują wyraźny wpływ przesunięcia płytki z dyszami na wyrównanie lokalnej wymiany ciepła z rozkładem naprężeń.
Wyniki dla przypadków 1 i 2 mogą się różnić o ponad 20 MPa pomiędzy maksymalnym a minimalnym naprężeniem oraz o 10 MPa w płaszczyźnie środkowej. Przykład 3 jest dużo bardziej jednorodny, a różnice naprężeń pomiędzy maksymalną a minimalną wartością nie przekraczają 5 MPa.
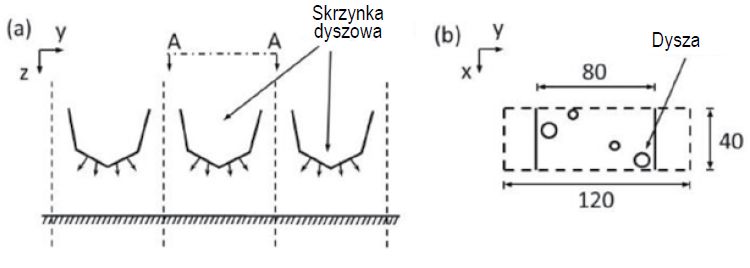
Rys. 6. Schemat dysz (a) oraz ich rozmieszczenie na płytce dyszy (b)
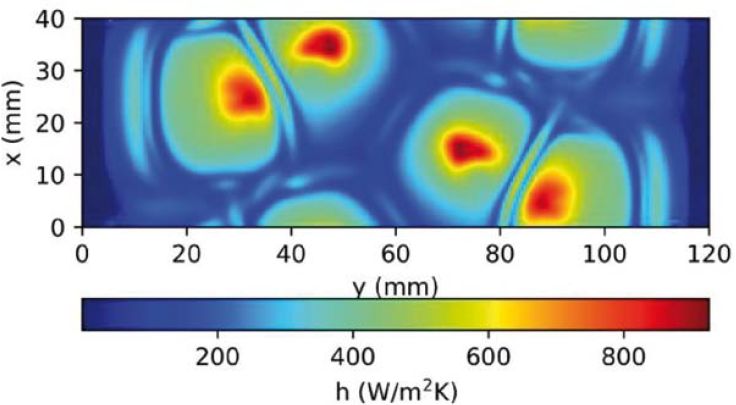
Rys. 7. Rozkład współczynnika wymiany ciepła w części A-A z rys. 6
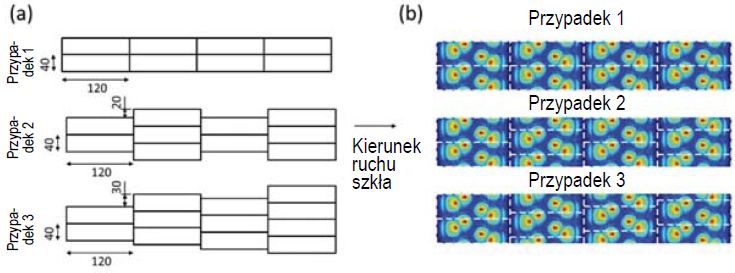
Rys. 8. Ilustracja cyklicznego położenia dysz oraz porównanie ze współczynnikiem wymiany ciepła (a) Schematy (b) Współczynniki wymiany ciepła. Wymiary podano w mm
Rys. 9. Modelowy obszar do symulacji naprężeń
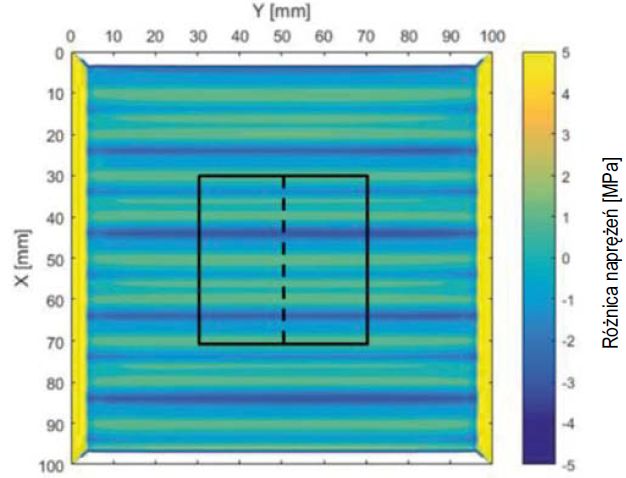
Rys. 10. Różnica naprężeń σx-σy na zewnętrznej powierzchni obszaru o wielkości 100x100 mm2, w 3 przypadku ustawienia dysz. Kwadrat po środku ilustruje obszar o wymiarach 40x40 mm2. Wyniki na rys. 11 i 12 zostały przedstawione przerywanymi liniami.
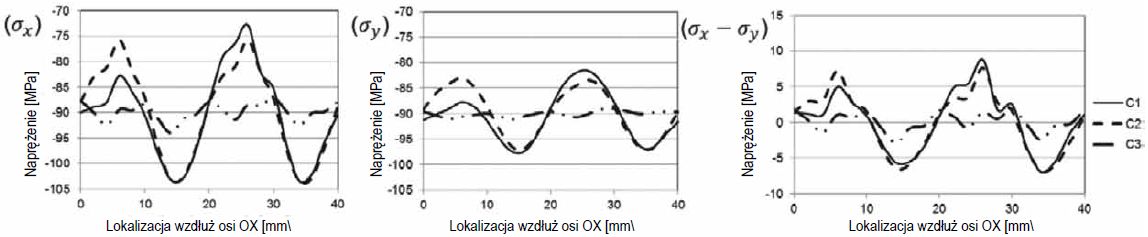
Rys. 11. Naprężenie ściskające σx, σy oraz σx-σy na powierzchni szkła wzdłuż przerywanej linii z rys. 10
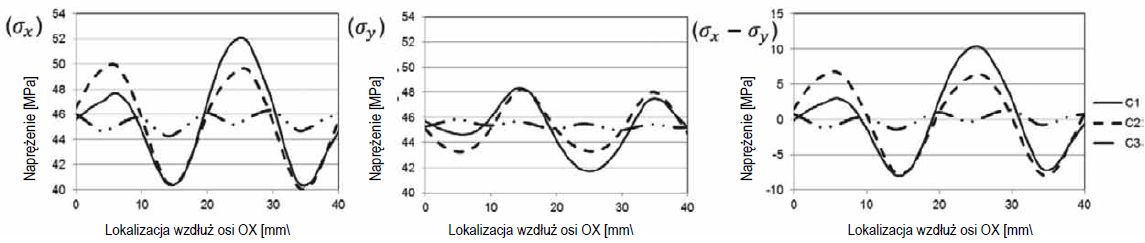
Rys. 12. Naprężenie rozciągające σx, σy oraz σx-σy na płaszczyźnie środkowej szkła wzdłuż przerywanej linii z rys. 10

Rys. 13. Rozkład anizotropii na szybie ze szkła hartowanego o wymiarach 585x800 mm2. Po prawej stronie znajduje się powiększony obszar o wymiarach 40x40 mm2, stanowiący obszar porównywalny do tego z rys. 10.
Obserwacje zjawiska anizotropii na hartowanym szkle
Wyniki naprężenia w modelu zostały porównane z rzeczywistym rozkładem zjawiska anizotropii zaobserwowanym w próbce testowej pokazanej na rys. 13. W eksperymencie hartowaniu poddano próbkę testową, utworzoną z przezroczystego szkła typu float o wymiarach 585x800 mm2 i grubości 3,85 mm.
Szkło najpierw podgrzano do około 630°C, a następnie ostudzono przy użyciu dyszowego systemu chłodzenia podobnego do tego z przypadku 3 w badaniu numerycznym. Nadciśnienie w skrzyni nadmuchowej wynosiło 5000 Pa, a odległość między dyszą a płaszczyzną – 16 mm.
W trakcie chłodzenia szkło przesuwane było z prędkością 450 mm/s. Naprężenie na powierzchni zmierzono przy użyciu polarymetru GASP do pomiaru naprężeń na powierzchni szkła. W zależności od miejsca naprężenie wynosiło pomiędzy 89 a 93 MPa.
Zjawisko anizotropii w próbce testowej zostało pokazane na rys. 13. W celu pokazania rozkładu anizotropii filtry polaryzujące oraz próbki szkła zostały ustawione w tym samym kierunku co na rys. 10.
Na rys. 13 zilustrowano porównanie wyników z badania numerycznego z wynikami eksperymentu. Zauważyć można na nim poziome, regularnie powtarzające się białe pasy.
W powiększonym oknie na rys. 13 widać trzy poziome pasy w równych odstępach. Szerokość każdego z nich to 40 mm, czyli tyle samo, co w badaniu numerycznym. Poziom naprężenia w rozkładzie zjawiska anizotropii nie jest dostępny.
Jednak, porównanie intensywności różnic w powiększonym obszarze na rys. 13 z intensywnością różnic na środku szyby na rys. 13 pokazuje, że zmiana naprężenia wynikająca z lokalizacji dysz jest mniejsza.
Wnioski
Optyczna jakość szkła hartowanego bez zjawiska anizotropii staje się coraz bardziej istotną kwestią, uwzględnianą w ocenie szkła hartowanego oraz maszyn do jego produkcji. Najważniejszym czynnikiem stojącym za jakością szkła jest kontrola wymiany ciepła, która powinna być równomierna na całej powierzchni szklanej oraz symetryczna w płaszczyźnie środkowej szkła.
W artykule pokazano, że dzięki najnowocześniejszym metodom obliczeniowej mechaniki płynów (CFD) możliwe jest wyliczenie wymiany ciepła w trakcie hartowania. Otrzymane w ten sposób wyniki można wykorzystać w programie wykorzystującym metodę elementów skończonych w celu obliczenia naprężeń wewnętrznych wywołanych przez wymianę ciepła.
Porównanie rozkładu naprężeń wewnętrznych uzyskanego w wyniku obliczeń z obserwacją szkła hartowanego przy użyciu polaryskopu pozwala zauważyć podobieństwa. Dzięki metodom numerycznym można zbadać zoptymalizować efekt, jaki umiejscowienie dysz ma na rozkład naprężeń.
Chociaż naprężenia wewnętrzne zanotowane w modelu oraz w eksperymencie są w dużej mierze analogiczne do zjawiska anizotropii zaobserwowanego na szkle hartowanym, nie można określić naprężenia na podstawie obrazu przedstawiającego zjawisko anizotropii.
Podziękowania
Autorzy pragną podziękować Finnish Funding Agency for Technology and Innovation (Tekes) za częściowe sfinansowanie niniejszej pracy w ramach programu Energy Efficient Tempering of Thin Glasses for Solar Energy Next Generation Products.
(...)
Autorzy pragną również złożyć podziękowania Uniwersytetowi w Sydney za udostępnienie usług HPC oraz oprogramowania, które przyczyniło się do uzyskania wyników badań przedstawionych w niniejszym artykule.
Artykuł opiera się na wykładzie prezentowanym Konferencji GLASS PERFORMANCE DAYS 2017, która odbyła się 28-30.06.2017 w Tampere, Finlandia
Antti Mikkonen
Uniwersytet Techniczny w Tampere, Finlandia
Antti Aronen
Uniwersytet w Sydney, Australia
Mikko Rantala
Glaston Finland Oy, Finlandia
Reijo Karvinen
Uniwersytet Techniczny w Tampere, Finlandia
Literatura
[1] Aronen, A. Karvinen, R.: Effect of initial temperature and cooling rate on residual stresses of tempered glass, Glass Structures & Engineering, na etapie recenzji.
[2] Illguth, M., Schuler, C., Bucak, Ö.: The Effect of Optical Anisotropies on Building Glass Façades and its Measurement Methods, “Frontiers of Architectural Research”, Vol. 4, pp. 119-126, 2015.
[3] Holger, M.: Heat and Mass Transfer between Impinging Gas Jets and Solid Surfaces, Advances in Heat Transfer, vol. 13, pp. 1-60, 1977.
[4] ANSYS®, Wersja 17.0
[5] The OpenFOAM foundation, http://www.openfoam.org/, wersja 4.0, 2017.
[6] Alimohammadi, S., Murray, D., Persoons T.: Experimental Validation of a Computational Fluid Dynamics Methodology for Transitional Flow Heat Transfer Characteristics of a Steady Impinging Jet, ASME. Journal of Heat Transfer, Vol. 136, 2014
[7] Menter, F. R., Kuntz, M., Langtry, R.: Ten Years of Industrial Experience with the SST Turbulence Model, Turbulence, Heat and Mass Transfer, Vol. 4, pp.625 – 632, 2003.
[8] Mikkonen, A., Karvinen, R.: Heat Transfer of Impinging Jet: Effect of Compressibility and Turbulent Kinetic Energy Production, IX International Conference on Computational Heat and Mass Transfer, 23-26 May 2016 Cracow, Poland, 2016.
[9] Zuckerman, N., Lior, N.: Jet Impingement Heat Transfer: Physics, Correlations, and Numerical Modeling, Advances in Heat Transfer, Vol. 39, pp.565– 631, 2006
[10] Flügge, W.: Viscoelasticity, 2nd ed., Springer- Verlag, Berlin, Germany, 1975.
[11] Scherer, G.: Relaxation in Glass and Composites, John Wiley & Sons, Inc., USA, 1986.
[12] Aronen, A.: Modelling of Deformations and Stresses in Glass Tempering, Dissertation, Tampere University of Technology, 2013.
[13] Gardon, R.: The Tempering of Flat Glass by Forced Convection, Proceedings VIIth International Congress on Glass, Brussels, Belgium, 1965.
[14] Aben, H., Guillemet, C.: Photoelasticity of Glass, Springer-Verlag, Germany, 1993.

Całość artykułu w wydaniu drukowanym i elektronicznym
Inne artykuły o podobnej tematyce patrz Serwisy Tematyczne
Więcej informacji: Świat Szkła 6/2019












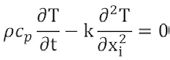 (1)
(1)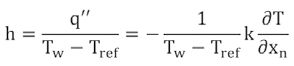 (2),
(2),
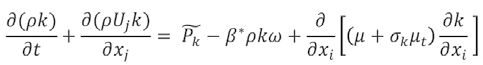 (3)
(3)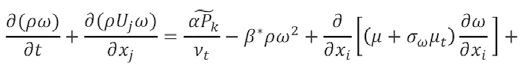
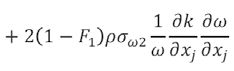 4)
4)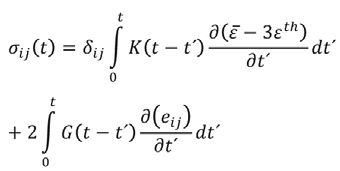 (5)
(5)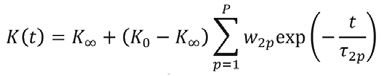 (6)
(6)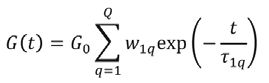 (7)
(7)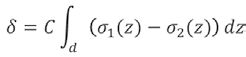 (13)
(13)































